人教版八年级数学下册20.1.1平均数同步课堂练习
文档属性
| 名称 | 人教版八年级数学下册20.1.1平均数同步课堂练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览


文档简介
人教版八年级数学下册第二十章数据的分析20.1.1同步课堂练习
一 选择题
1.2012年5月某日我国部分城市的最高气温统计如下表所示:
城市
武汉
成都
北京
上海
海南
南京
拉萨
深圳
气温(℃)
27
27
24
25
28
28
23
26
请问这组数据的平均数是( )
A.24 B.25 C.26 D.27
2.地球的水资源越来越枯竭,全世界都提倡节约用水,小明把自己家1月至6月份的用水量绘制成折线图,那么小明家这6个月的月平均用水量是( ).
A.10吨 B.9吨 C.8吨 D.7吨
3.我省某市五月份第二周连续七天的空气质量指数分别为:111、96、47、68、70、77、105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
4.某棵果树前x年的总产量y与x之间的关系如图所示,从目前记录的结果看,前x年的年平均产量最高,则x的值为( )
A.3 B.5 C.7 D.9
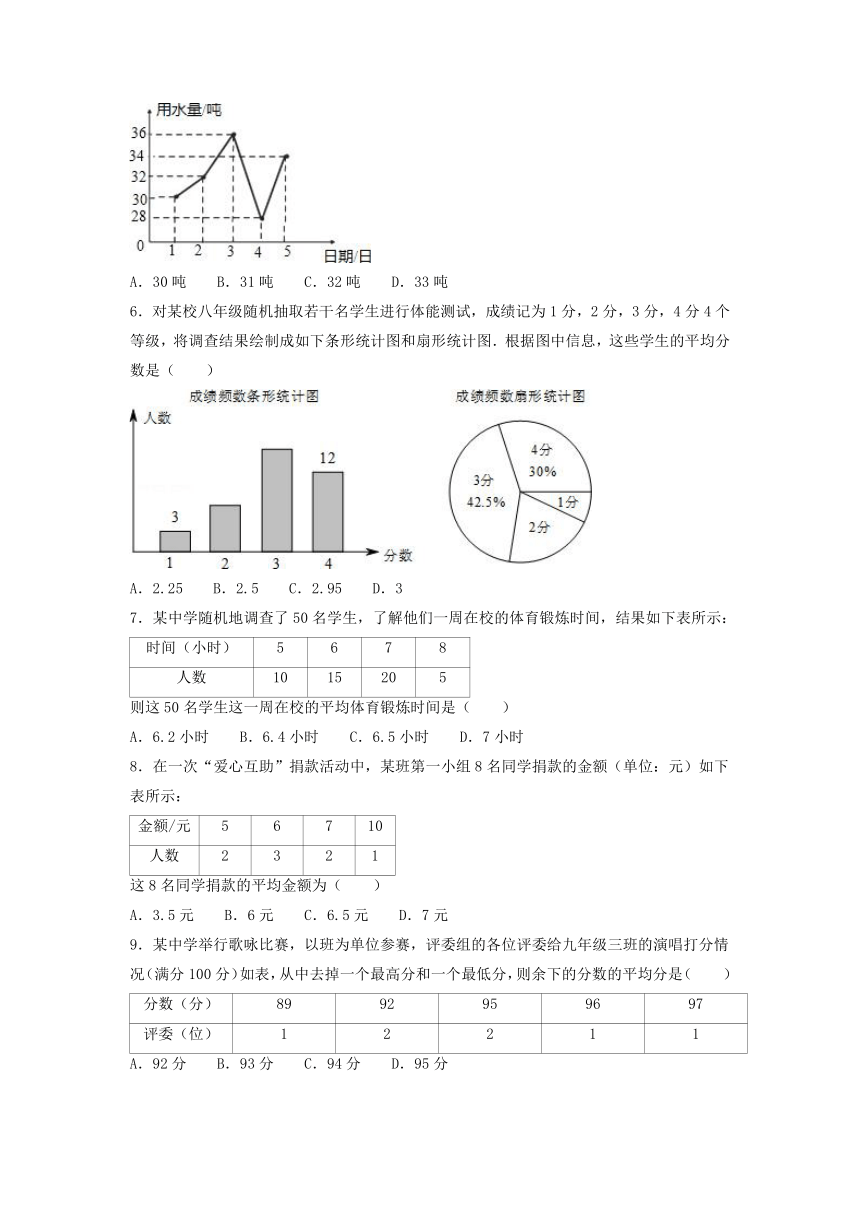
5.某住宅小区六月份1日至5日每天用水量变化情况如图所示.那么这5天平均每天的用水量是( )
A.30吨 B.31吨 C.32吨 D.33吨
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( )
A.2.25 B.2.5 C.2.95 D.3
7.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间(小时)
5
6
7
8
人数
10
15
20
5
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2小时 B.6.4小时 C.6.5小时 D.7小时
8.在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:
金额/元
5
6
7
10
人数
2
3
2
1
这8名同学捐款的平均金额为( )
A.3.5元 B.6元 C.6.5元 D.7元
9.某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打分情况(满分100分)如表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( )
分数(分)
89
92
95
96
97
评委(位)
1
2
2
1
1
A.92分 B.93分 C.94分 D.95分
10.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
节水量/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
11.某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5 B.6 C.0.5 D.-6
12.某同学用计算器计算30个数据时,错将其中一个数据105输入15,那么由此求出的平均数与实际平均数的差是( )
A.3.5 B.3 C.-3 D.0.5
13.用计算器求一组数据21,22,25,23,27,19,24,20,25,24,18,27的平均数是(保留一位小数)( )
A.22.7 B.22.8 C.22.9 D.23.0
14.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B.14.16 C.14.17 D.14.20
二 填空题
15.若数2,3,x,5,6五个数的平均数为4,则x的值为 .
16.在演唱比赛中,5位评委给一位歌手的打分如下:8.2分,8.3分,7.8分,7.7分,8.0分,则这位歌手的平均得分是 分.
17.若数据2,3,-1,7,x的平均数为2,则x= .
18.某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:
时间(单位:小时)
4
3
2
1
0
人数
2
4
2
1
1
则这10名学生周末利用网络进行学习的平均时间是 小时.
19.某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.
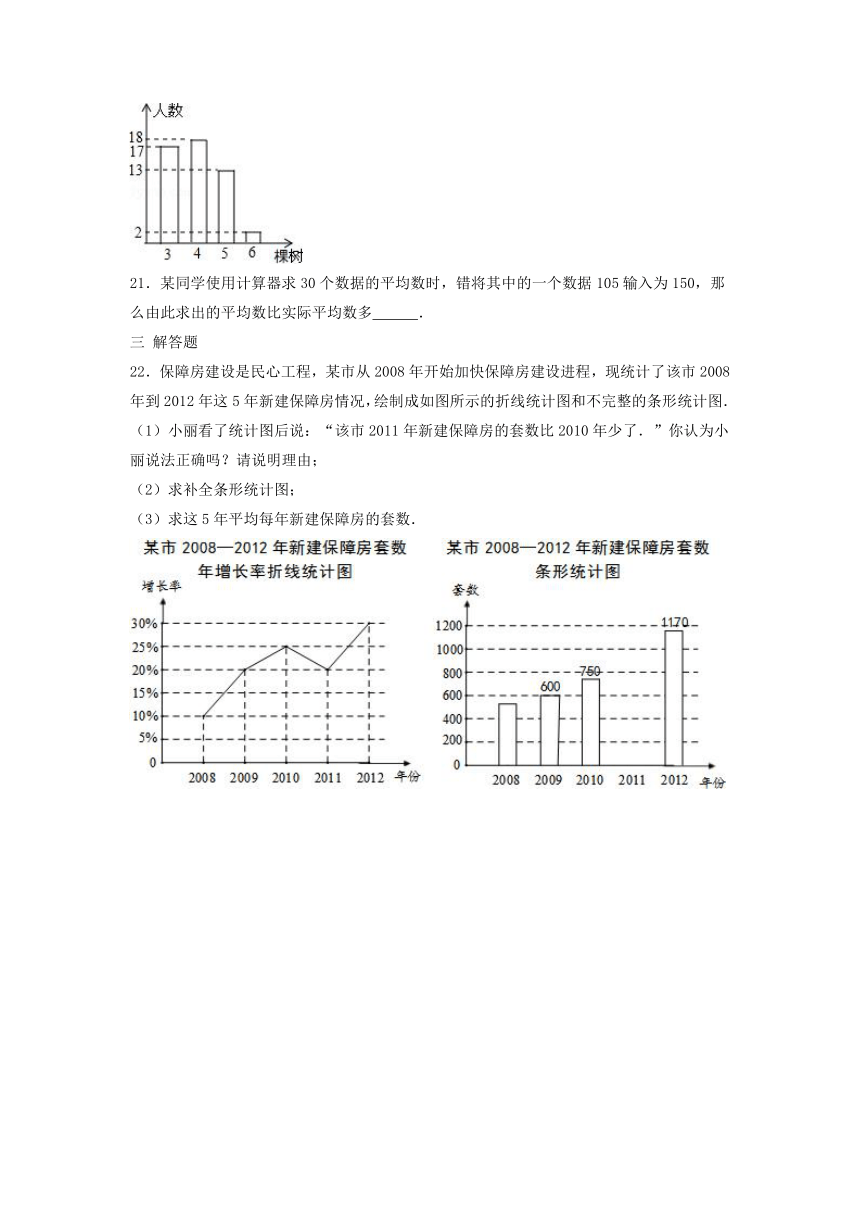
20.某校九年级420名学生参加植树活动,随机调查了50名学生植树的数量,并根据数据绘制了如下条形统计图,请估计该校九年级学生此次植树活动约植树 棵.
21.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为150,那么由此求出的平均数比实际平均数多 .
三 解答题
22.保障房建设是民心工程,某市从2008年开始加快保障房建设进程,现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
23.已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将x吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
运输工具
运输费单价
元/(吨?千米)
冷藏费单价
元/(吨?时)
固定费用
元/次
汽车
2
5
200
火车
1.6
5
2280
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与 x的函数关系式(不必写出x的取值范围),及x为何值时y汽>y火 (总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
24.某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
25.某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
候选人
百分制
教学技能考核成绩
专业知识考核成绩
甲
85
92
乙
91
85
丙
80
90
(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人 将被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
人教版八年级数学下册第二十章数据的分析20.1.1同步课堂练习试题答案
C 2.A 3.C 4.C 5.C 6.C 7.B 8.C 9.C 10.A 11.B 12.C 13.C 14.B
4 16. 8 17. -1 18. 2.5 19. 88 20. 1680 21. 1.5
22.解:(1)该市2011年新建保障房的增长率比2010年的增长率减少了,
但是保障房的总数在增加,故小丽的说法错误;
(2)2011年保障房的套数为:750×(1+20%)=900(套),
2008年保障房的套数为:x(1+20%)=600,则x=500,
补图略.
(3)这5年平均每年新建保障房的套数为:(500+600+750+900+1170)÷5=784(套),
答:这5年平均每年新建保障房的套数为784套.
23.(1)根据图表上点的坐标为:(2,120),(2,200),
∴汽车的速度为 60千米/时,火车的速度为 100千米/时,
故答案为:60,100;
(2)依据题意得出:y汽=240·2x+·5x+200=500x+200;
y火=240×1.6x+·5x+2280=396x+2280.
若y汽>y火,得出500x+200>396x+2280.∴x>20;
(3)上周货运量=(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省.
从折线图走势分析,上周货运量周四(含周四)后大于20且呈上升趋势,建议预订火车费用较省.
24.(1)甲的总分为:66×10%+89×40%+86×20%+68×30%=79.8
(2)由图表可知甲,乙,丙的七巧板拼图,魔方复原分数均相同,设趣题巧解以及数学应用比重为x,y
解得
∴甲的得分为20+89×0.3+86×0.4=81.1>80
∴甲能获得一等奖
25.(1)甲。
(2)根据题意得:
甲的平均成绩为:(85×6+92×4)÷10=87.8(分),
乙的平均成绩为:(91×6+85×4)÷10=88.6(分),
丙的平均成绩为:(80×6+90×4)÷10=84(分),
∵乙的平均分数最高,∴乙将被录取。
一 选择题
1.2012年5月某日我国部分城市的最高气温统计如下表所示:
城市
武汉
成都
北京
上海
海南
南京
拉萨
深圳
气温(℃)
27
27
24
25
28
28
23
26
请问这组数据的平均数是( )
A.24 B.25 C.26 D.27
2.地球的水资源越来越枯竭,全世界都提倡节约用水,小明把自己家1月至6月份的用水量绘制成折线图,那么小明家这6个月的月平均用水量是( ).
A.10吨 B.9吨 C.8吨 D.7吨
3.我省某市五月份第二周连续七天的空气质量指数分别为:111、96、47、68、70、77、105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
4.某棵果树前x年的总产量y与x之间的关系如图所示,从目前记录的结果看,前x年的年平均产量最高,则x的值为( )
A.3 B.5 C.7 D.9
5.某住宅小区六月份1日至5日每天用水量变化情况如图所示.那么这5天平均每天的用水量是( )
A.30吨 B.31吨 C.32吨 D.33吨
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( )
A.2.25 B.2.5 C.2.95 D.3
7.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间(小时)
5
6
7
8
人数
10
15
20
5
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2小时 B.6.4小时 C.6.5小时 D.7小时
8.在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:
金额/元
5
6
7
10
人数
2
3
2
1
这8名同学捐款的平均金额为( )
A.3.5元 B.6元 C.6.5元 D.7元
9.某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打分情况(满分100分)如表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( )
分数(分)
89
92
95
96
97
评委(位)
1
2
2
1
1
A.92分 B.93分 C.94分 D.95分
10.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
节水量/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
11.某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5 B.6 C.0.5 D.-6
12.某同学用计算器计算30个数据时,错将其中一个数据105输入15,那么由此求出的平均数与实际平均数的差是( )
A.3.5 B.3 C.-3 D.0.5
13.用计算器求一组数据21,22,25,23,27,19,24,20,25,24,18,27的平均数是(保留一位小数)( )
A.22.7 B.22.8 C.22.9 D.23.0
14.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B.14.16 C.14.17 D.14.20
二 填空题
15.若数2,3,x,5,6五个数的平均数为4,则x的值为 .
16.在演唱比赛中,5位评委给一位歌手的打分如下:8.2分,8.3分,7.8分,7.7分,8.0分,则这位歌手的平均得分是 分.
17.若数据2,3,-1,7,x的平均数为2,则x= .
18.某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:
时间(单位:小时)
4
3
2
1
0
人数
2
4
2
1
1
则这10名学生周末利用网络进行学习的平均时间是 小时.
19.某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.
20.某校九年级420名学生参加植树活动,随机调查了50名学生植树的数量,并根据数据绘制了如下条形统计图,请估计该校九年级学生此次植树活动约植树 棵.
21.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为150,那么由此求出的平均数比实际平均数多 .
三 解答题
22.保障房建设是民心工程,某市从2008年开始加快保障房建设进程,现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
23.已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将x吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
运输工具
运输费单价
元/(吨?千米)
冷藏费单价
元/(吨?时)
固定费用
元/次
汽车
2
5
200
火车
1.6
5
2280
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与 x的函数关系式(不必写出x的取值范围),及x为何值时y汽>y火 (总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
24.某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
25.某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
候选人
百分制
教学技能考核成绩
专业知识考核成绩
甲
85
92
乙
91
85
丙
80
90
(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人 将被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
人教版八年级数学下册第二十章数据的分析20.1.1同步课堂练习试题答案
C 2.A 3.C 4.C 5.C 6.C 7.B 8.C 9.C 10.A 11.B 12.C 13.C 14.B
4 16. 8 17. -1 18. 2.5 19. 88 20. 1680 21. 1.5
22.解:(1)该市2011年新建保障房的增长率比2010年的增长率减少了,
但是保障房的总数在增加,故小丽的说法错误;
(2)2011年保障房的套数为:750×(1+20%)=900(套),
2008年保障房的套数为:x(1+20%)=600,则x=500,
补图略.
(3)这5年平均每年新建保障房的套数为:(500+600+750+900+1170)÷5=784(套),
答:这5年平均每年新建保障房的套数为784套.
23.(1)根据图表上点的坐标为:(2,120),(2,200),
∴汽车的速度为 60千米/时,火车的速度为 100千米/时,
故答案为:60,100;
(2)依据题意得出:y汽=240·2x+·5x+200=500x+200;
y火=240×1.6x+·5x+2280=396x+2280.
若y汽>y火,得出500x+200>396x+2280.∴x>20;
(3)上周货运量=(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省.
从折线图走势分析,上周货运量周四(含周四)后大于20且呈上升趋势,建议预订火车费用较省.
24.(1)甲的总分为:66×10%+89×40%+86×20%+68×30%=79.8
(2)由图表可知甲,乙,丙的七巧板拼图,魔方复原分数均相同,设趣题巧解以及数学应用比重为x,y
解得
∴甲的得分为20+89×0.3+86×0.4=81.1>80
∴甲能获得一等奖
25.(1)甲。
(2)根据题意得:
甲的平均成绩为:(85×6+92×4)÷10=87.8(分),
乙的平均成绩为:(91×6+85×4)÷10=88.6(分),
丙的平均成绩为:(80×6+90×4)÷10=84(分),
∵乙的平均分数最高,∴乙将被录取。
