18.1.1 第1课时平行四边形的边、角的特征同步练习(附答案)
文档属性
| 名称 | 18.1.1 第1课时平行四边形的边、角的特征同步练习(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十八章 平行四边形
18.1.1第1课时 平行四边形的边、角的特征 同步练习
一、单选题
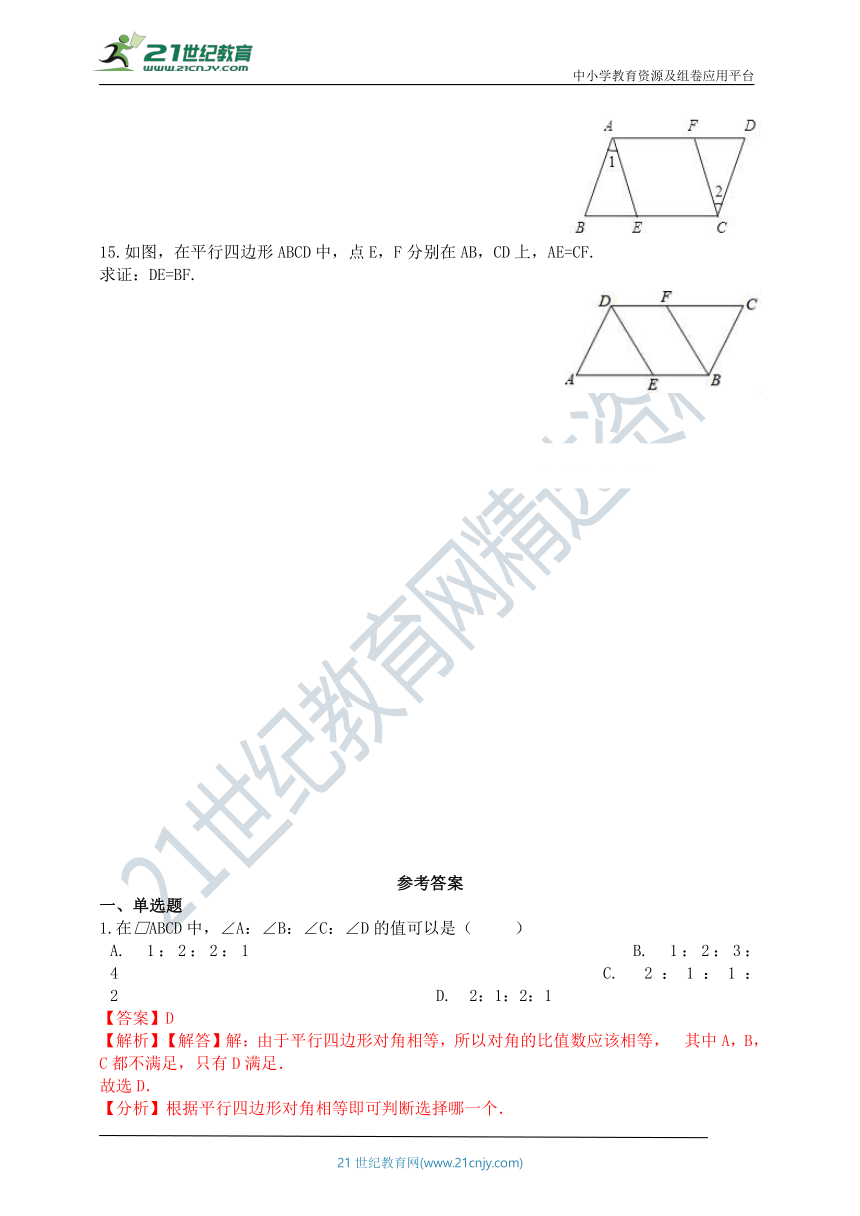
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是(?? )
A.?1:2:2:1???????????????????B.?1:2:3:4???????????????????C.?2:1:1:2???????????????????D.?2:1:2:1
2.在?ABCD中,∠A=2∠D,则∠C的度数为(?? )
A.?30°??????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????D.?120°
3.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的 ,那么BC的长是(?? )
A.?6??????????????????????????????????B.?8????????????????????????????????????C.?10?????????????????????????????????????D.?16
4.下列结论中,平行四边形不一定具备的是( )
A.?对角相等??????????????????????B.?对角互补???????????????????????C.?邻角互补?????????????????????D.?内角和是360°
5.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( ??)
A.?13?????????????????????????????????????????B.?17?????????????????????????????????????????C.?20?????????????????????????????????????????D.?26
6.已知□ABCD中,∠A+∠C=240°,则∠B的度数是(?? ).
A.?100°?????????????????????????????????B.?160°?????????????????????????????????C.?80°??????????????????????????????????D.?60°
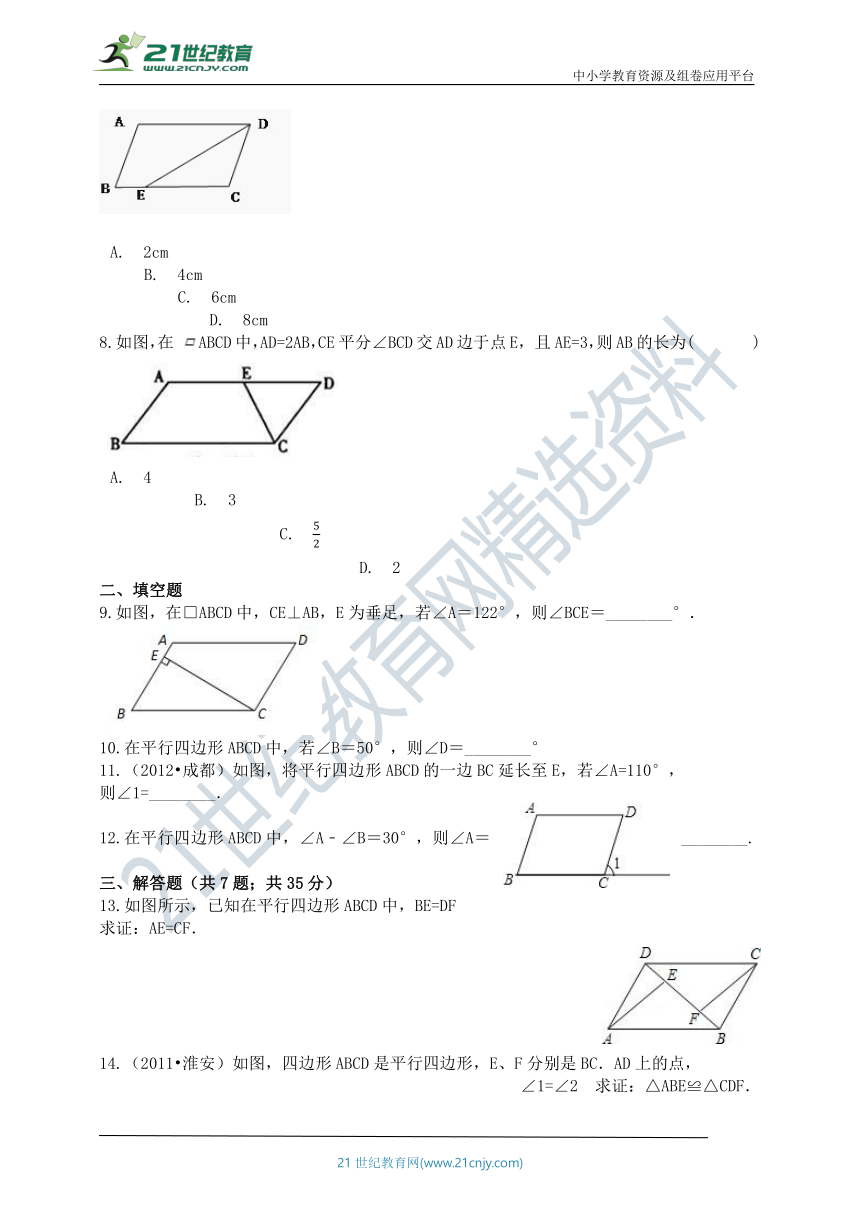
7.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E , 则BE等于( ).
A.?2cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
8.如图,在 ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(??? )
A.?4?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2
二、填空题
9.如图,在□ABCD中,CE⊥AB,E为垂足,若∠A=122°,则∠BCE=________°.
10.在平行四边形ABCD中,若∠B=50°,则∠D=________°
11.(2012?成都)如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,
则∠1=________.
12.在平行四边形ABCD中,∠A﹣∠B=30°,则∠A=________.
三、解答题(共7题;共35分)
13.如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
14.(2011?淮安)如图,四边形ABCD是平行四边形,E、F分别是BC.AD上的点,
∠1=∠2 求证:△ABE≌△CDF.
15.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.
求证:DE=BF.
参考答案
一、单选题
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是(?? )
A.?1:2:2:1???????????????????B.?1:2:3:4???????????????????C.?2:1:1:2???????????????????D.?2:1:2:1
【答案】D
【解析】【解答】解:由于平行四边形对角相等,所以对角的比值数应该相等, 其中A,B,C都不满足,只有D满足.
故选D.
【分析】根据平行四边形对角相等即可判断选择哪一个.
2.在?ABCD中,∠A=2∠D,则∠C的度数为(?? )
A.?30°??????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????D.?120°
【答案】 D
【解析】【解答】解:画出图形如下所示:
∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,
又∠A=2∠D ,
∴∠A=120°,∠D=60°,
∴∠C=∠A=120°,
故答案为:D.
【分析】根据平行四边形的邻角互补,可得∠A+∠D=180°,由∠A=2∠D,联立即可求出∠A的度数,利用平行四边形的对角相等,即可求出∠C.
3.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的 ,那么BC的长是(?? )
A.?6??????????????????????????????????B.?8????????????????????????????????????C.?10?????????????????????????????????????D.?16
【答案】 C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ?,
∴四边形ABCD周长为:6÷ =32,
∴AB+BC= ×32=16,
∴BC=10.
故答案为:C.
【分析】根据AB的长及它所占周长的比例,可求出平行四边形ABCD的周长,然后利用平行四边形对边相等求出BC。
4.下列结论中,平行四边形不一定具备的是( )
A.?对角相等??????????????????????B.?对角互补???????????????????????C.?邻角互补?????????????????????D.?内角和是360°
【答案】 B
【解析】【分析】根据平行四边形的性质可知:B、C均是平行四边形的性质;根据多边形内角和定理可知:四边形内角和是360°,即D也正确;唯有B是平行四边形不一定具备的性质。
故选B.
5.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( ??)
A.?13?????????????????????????????????????????B.?17?????????????????????????????????????????C.?20?????????????????????????????????????????D.?26
【答案】B
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17.
故答案为:B.
【分析】根据平行四边形的对角线互相平分,对边相等得出OA=OC=3,OB=OD=6,BC=AD=8,再根据三角形的周长计算方法计算出结果即可。
6.已知□ABCD中,∠A+∠C=240°,则∠B的度数是(?? ).
A.?100°?????????????????????????????????B.?160°?????????????????????????????????C.?80°??????????????????????????????????D.?60°
【答案】 D
【解析】【解答】已知□ABCD中,∠A+∠C=240°,根据平行四边形的对角相等可得∠A=∠C=120°,再由邻角互补可得∠B=60°,
故答案为:D.
【分析】根据平行四边形的对角相等及邻角互补的性质,选确定∠A的度数,即可求出∠B的度数.
7.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E , 则BE等于( ).
A.?2cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
【答案】 A
【解析】【解答】∵ 四边形ABCD是平行四边形,
∴AD∥BC ,
∴∠CED=∠ADE ,
∵DE平分∠ADC交BC边于点E , AD=8㎝, AB=6㎝,
∴∠CED=∠CDE ,
∴CE=CD=AB=6cm,
∴BE=2㎝,
故选A.
【分析】先根据两直线平行,内错角相等和角平分线的定义得到∠CED=∠CDE , 再利用等角对等边得到CE=CD , 从而求得BE的值.
8.如图,在 ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(??? )
A.?4?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2
【答案】 B
【解析】【解答】解:∵CE平分∠BCD,∴∠BCE=∠ECD,∵AD∥BC,∴∠BCE=∠DEC,∴ED=DC,又∵2AB=AD,∴AE+ED=3+AB,∴AB=3.
故答案为:B
二、填空题
9.如图,在□ABCD中,CE⊥AB,E为垂足,若∠A=122°,则∠BCE=________°.
【答案】 32
【解析】【解答】? ∵AD∥BC, ∴∠B=180-∠A=180°-122°=58°.
∴∠BCE=90°-58°=32°.
【分析】根据平行四边形的对边平行得出AD∥BC, 根据二直线平行,同旁内角互补算出∠B的度数,最后根据三角形的内角和即可算出答案。
10.在平行四边形ABCD中,若∠B=50°,则∠D=________°
【答案】 50
【解析】【解答】根据“平行四边形的对角相等”可知:∠D=∠B=50°.
故答案为:50.
【分析】由平行四边形的对角相等可求解。
11.(2012?成都)如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,
则∠1=________.
【答案】70°
【解析】【解答】解:∵平行四边形ABCD的∠A=110°, ∴∠BCD=∠A=110°,
∴∠1=180°﹣∠BCD=180°﹣110°=70°.
故答案为:70°.
【分析】根据平行四边形的对角相等求出∠BCD的度数,再根据平角等于180°列式计算即可得解.
12.在平行四边形ABCD中,∠A﹣∠B=30°,则∠A=________.
【答案】 105°
【解析】【解答】∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AD ∥ BC,
∴∠A+∠B=180°,
∵∠A-∠B=30°,
∴∠A=105°,
故答案为:105°.
【分析】根据平行四边形的对角相等和对边平行可得∠A=∠C,∠B=∠D,AD ∥ BC,再根据两直线平行同旁内角互补可得∠A+∠B=180°,再根据∠A-∠B=30°即可求解.
三、解答题(共7题;共35分)
13.如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
【答案】 证明:∵BE=DF,
∴BE﹣EF=DF﹣EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】【分析】由BE=DF,可得DE=BF,在平行四边形ABCD中有AD=BC,AD∥BC,故可由两直线平行内错角相等可得∠ADE=∠CBF,从而可利用SAS证得△ADE≌△CBF,即可由全等三角形的对应边相等得到AE=CF.
14.(2011?淮安)如图,四边形ABCD是平行四边形,E、F分别是BC.AD上的点,
∠1=∠2 求证:△ABE≌△CDF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,
在:△ABE与△CDF中,
∴△ABE≌△CDF(ASA)
【解析】【分析】利用平行四边形的性质和题目提供的相等的角可以为证明三角形全等提供足够的条件.
15.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.
求证:DE=BF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中, ,
∴△ADE≌△CBF(SAS),
∴DE=BF.
【解析】【分析】由平行四边形的性质,可证得△ADE≌△CDF,则可证得DE=BF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十八章 平行四边形
18.1.1第1课时 平行四边形的边、角的特征 同步练习
一、单选题
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是(?? )
A.?1:2:2:1???????????????????B.?1:2:3:4???????????????????C.?2:1:1:2???????????????????D.?2:1:2:1
2.在?ABCD中,∠A=2∠D,则∠C的度数为(?? )
A.?30°??????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????D.?120°
3.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的 ,那么BC的长是(?? )
A.?6??????????????????????????????????B.?8????????????????????????????????????C.?10?????????????????????????????????????D.?16
4.下列结论中,平行四边形不一定具备的是( )
A.?对角相等??????????????????????B.?对角互补???????????????????????C.?邻角互补?????????????????????D.?内角和是360°
5.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( ??)
A.?13?????????????????????????????????????????B.?17?????????????????????????????????????????C.?20?????????????????????????????????????????D.?26
6.已知□ABCD中,∠A+∠C=240°,则∠B的度数是(?? ).
A.?100°?????????????????????????????????B.?160°?????????????????????????????????C.?80°??????????????????????????????????D.?60°
7.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E , 则BE等于( ).
A.?2cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
8.如图,在 ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(??? )
A.?4?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2
二、填空题
9.如图,在□ABCD中,CE⊥AB,E为垂足,若∠A=122°,则∠BCE=________°.
10.在平行四边形ABCD中,若∠B=50°,则∠D=________°
11.(2012?成都)如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,
则∠1=________.
12.在平行四边形ABCD中,∠A﹣∠B=30°,则∠A=________.
三、解答题(共7题;共35分)
13.如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
14.(2011?淮安)如图,四边形ABCD是平行四边形,E、F分别是BC.AD上的点,
∠1=∠2 求证:△ABE≌△CDF.
15.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.
求证:DE=BF.
参考答案
一、单选题
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是(?? )
A.?1:2:2:1???????????????????B.?1:2:3:4???????????????????C.?2:1:1:2???????????????????D.?2:1:2:1
【答案】D
【解析】【解答】解:由于平行四边形对角相等,所以对角的比值数应该相等, 其中A,B,C都不满足,只有D满足.
故选D.
【分析】根据平行四边形对角相等即可判断选择哪一个.
2.在?ABCD中,∠A=2∠D,则∠C的度数为(?? )
A.?30°??????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????D.?120°
【答案】 D
【解析】【解答】解:画出图形如下所示:
∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,
又∠A=2∠D ,
∴∠A=120°,∠D=60°,
∴∠C=∠A=120°,
故答案为:D.
【分析】根据平行四边形的邻角互补,可得∠A+∠D=180°,由∠A=2∠D,联立即可求出∠A的度数,利用平行四边形的对角相等,即可求出∠C.
3.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的 ,那么BC的长是(?? )
A.?6??????????????????????????????????B.?8????????????????????????????????????C.?10?????????????????????????????????????D.?16
【答案】 C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ?,
∴四边形ABCD周长为:6÷ =32,
∴AB+BC= ×32=16,
∴BC=10.
故答案为:C.
【分析】根据AB的长及它所占周长的比例,可求出平行四边形ABCD的周长,然后利用平行四边形对边相等求出BC。
4.下列结论中,平行四边形不一定具备的是( )
A.?对角相等??????????????????????B.?对角互补???????????????????????C.?邻角互补?????????????????????D.?内角和是360°
【答案】 B
【解析】【分析】根据平行四边形的性质可知:B、C均是平行四边形的性质;根据多边形内角和定理可知:四边形内角和是360°,即D也正确;唯有B是平行四边形不一定具备的性质。
故选B.
5.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( ??)
A.?13?????????????????????????????????????????B.?17?????????????????????????????????????????C.?20?????????????????????????????????????????D.?26
【答案】B
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17.
故答案为:B.
【分析】根据平行四边形的对角线互相平分,对边相等得出OA=OC=3,OB=OD=6,BC=AD=8,再根据三角形的周长计算方法计算出结果即可。
6.已知□ABCD中,∠A+∠C=240°,则∠B的度数是(?? ).
A.?100°?????????????????????????????????B.?160°?????????????????????????????????C.?80°??????????????????????????????????D.?60°
【答案】 D
【解析】【解答】已知□ABCD中,∠A+∠C=240°,根据平行四边形的对角相等可得∠A=∠C=120°,再由邻角互补可得∠B=60°,
故答案为:D.
【分析】根据平行四边形的对角相等及邻角互补的性质,选确定∠A的度数,即可求出∠B的度数.
7.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E , 则BE等于( ).
A.?2cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
【答案】 A
【解析】【解答】∵ 四边形ABCD是平行四边形,
∴AD∥BC ,
∴∠CED=∠ADE ,
∵DE平分∠ADC交BC边于点E , AD=8㎝, AB=6㎝,
∴∠CED=∠CDE ,
∴CE=CD=AB=6cm,
∴BE=2㎝,
故选A.
【分析】先根据两直线平行,内错角相等和角平分线的定义得到∠CED=∠CDE , 再利用等角对等边得到CE=CD , 从而求得BE的值.
8.如图,在 ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(??? )
A.?4?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2
【答案】 B
【解析】【解答】解:∵CE平分∠BCD,∴∠BCE=∠ECD,∵AD∥BC,∴∠BCE=∠DEC,∴ED=DC,又∵2AB=AD,∴AE+ED=3+AB,∴AB=3.
故答案为:B
二、填空题
9.如图,在□ABCD中,CE⊥AB,E为垂足,若∠A=122°,则∠BCE=________°.
【答案】 32
【解析】【解答】? ∵AD∥BC, ∴∠B=180-∠A=180°-122°=58°.
∴∠BCE=90°-58°=32°.
【分析】根据平行四边形的对边平行得出AD∥BC, 根据二直线平行,同旁内角互补算出∠B的度数,最后根据三角形的内角和即可算出答案。
10.在平行四边形ABCD中,若∠B=50°,则∠D=________°
【答案】 50
【解析】【解答】根据“平行四边形的对角相等”可知:∠D=∠B=50°.
故答案为:50.
【分析】由平行四边形的对角相等可求解。
11.(2012?成都)如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,
则∠1=________.
【答案】70°
【解析】【解答】解:∵平行四边形ABCD的∠A=110°, ∴∠BCD=∠A=110°,
∴∠1=180°﹣∠BCD=180°﹣110°=70°.
故答案为:70°.
【分析】根据平行四边形的对角相等求出∠BCD的度数,再根据平角等于180°列式计算即可得解.
12.在平行四边形ABCD中,∠A﹣∠B=30°,则∠A=________.
【答案】 105°
【解析】【解答】∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AD ∥ BC,
∴∠A+∠B=180°,
∵∠A-∠B=30°,
∴∠A=105°,
故答案为:105°.
【分析】根据平行四边形的对角相等和对边平行可得∠A=∠C,∠B=∠D,AD ∥ BC,再根据两直线平行同旁内角互补可得∠A+∠B=180°,再根据∠A-∠B=30°即可求解.
三、解答题(共7题;共35分)
13.如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
【答案】 证明:∵BE=DF,
∴BE﹣EF=DF﹣EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】【分析】由BE=DF,可得DE=BF,在平行四边形ABCD中有AD=BC,AD∥BC,故可由两直线平行内错角相等可得∠ADE=∠CBF,从而可利用SAS证得△ADE≌△CBF,即可由全等三角形的对应边相等得到AE=CF.
14.(2011?淮安)如图,四边形ABCD是平行四边形,E、F分别是BC.AD上的点,
∠1=∠2 求证:△ABE≌△CDF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,
在:△ABE与△CDF中,
∴△ABE≌△CDF(ASA)
【解析】【分析】利用平行四边形的性质和题目提供的相等的角可以为证明三角形全等提供足够的条件.
15.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.
求证:DE=BF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中, ,
∴△ADE≌△CBF(SAS),
∴DE=BF.
【解析】【分析】由平行四边形的性质,可证得△ADE≌△CDF,则可证得DE=BF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
