18.1.1 第2课时平行四边形对角线的特征同步练习(附答案)
文档属性
| 名称 | 18.1.1 第2课时平行四边形对角线的特征同步练习(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十八章 平行四边形
18.1.1第2课时 平行四边形对角线的特征 同步练习
一、单选题
1.平行四边形所具有的性质是(?? )
A.?对角线相等????????? ??B.?邻边互相垂直??????????
?C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在□ABCD中,E是AB延长线上的一点,若∠1=60°,则∠A的度数为(???).
A.?120°?????????????????????????????????????B.?60°????????????????????????????????C.?45°???????????????????????????????????D.?30°
3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是(?? )
A.?AC⊥BD????????????????????????????B.?AO=OD??????????????????????????
??C.?AC=BD????????????????????????????D.?OA=OC
4.如图,在?ABCD中,AE平分∠DAB,AB=5,DE=2.则?ABCD的周长是(??? )
A.?7?????????????????????????????????????B.?10???????????????????????????????????C.?14????????????????????????????????????????D.?16
5.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(?? )
A.?4<x<6?????????????????????????B.?2<x<8?????????????????????????C.?0<x<10?????????????????????????D.?0<x<6
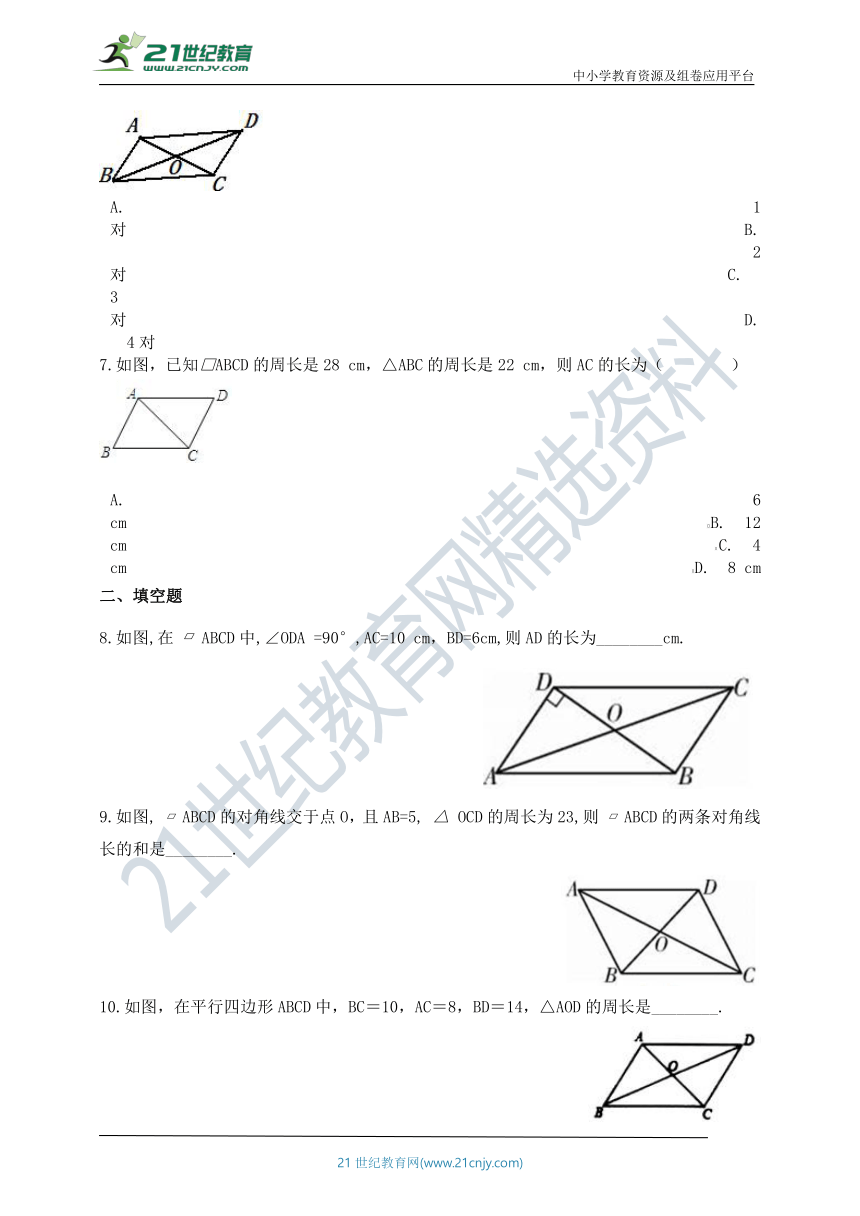
6.如图,如果□ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有(?? )
A.?1对?????????????????????????????????????B.?2对????????????????????????????????????C.?3对?????????????????????????????????????D.?4对
7.如图,已知□ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为(????)
A.?6 cm??????????????????????????????????B.?12 cm??????????????????????????????????C.?4 cm??????????????????????????????????D.?8 cm
二、填空题
8.如图,在 ABCD中,∠ODA =90°,AC=10 cm,BD=6cm,则AD的长为________cm.
9.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________.
10.如图,在平行四边形ABCD中,BC=10,AC=8,BD=14,△AOD的周长是________.
三、解答题
11.已知:如图,□ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F,求证:AE=CF.
12.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.
参考答案
一、单选题
1.平行四边形所具有的性质是(?? )
A.?对角线相等????????? ??B.?邻边互相垂直??????????
?C.?每条对角线平分一组对角???????????D.?两组对边分别相等
【答案】 D
【解析】【解答】平行四边形的对角相等,对角线互相平分,对边平行且相等.
故答案为:D.
【分析】平行四边形的性质:对边平行且相等,对角线互相平分,对角相等,邻角互补,据此判断即可.
2.在□ABCD中,E是AB延长线上的一点,若∠1=60°,则∠A的度数为(???).
A.?120°?????????????????????????????????????B.?60°????????????????????????????????C.?45°???????????????????????????????????D.?30°
【答案】B
【解析】
【分析】根据平行四边形的性质:平行四边形的对边平行.由?ABCD可知AD∥BC,所以
∠1=∠A=60°.
【解答】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠A=60°.
故选:B.
3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是(?? )
A.?AC⊥BD????????????????????????????B.?AO=OD??????????????????????????
??C.?AC=BD????????????????????????????D.?OA=OC
【答案】D
【解析】【解答】A、菱形的对角线才相互垂直,A不符合题意;
B、平行四边形中,AO不一定等于OD,B不符合题意;
C、只有平行四边形为矩形时,其对角线相等,C不符合题意;
D、平行四边形对角线互相平分,D符合题意;.
故答案为:D.
【分析】根据平行四边形的性质判断.平行四边形的对角线互相平分.
4.如图,在?ABCD中,AE平分∠DAB,AB=5,DE=2.则?ABCD的周长是(??? )
A.?7??????????????????????????????????????B.?10????????????????????????????????????C.?14?????????????????????????????????????????D.?16
【答案】C
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=5,AB∥CD,BC=AD,
∴∠AED=∠BAE,
又∵AE平分∠DAB,
∴∠DAE=∠BAE.
∴∠DAE=∠AED.
∴AD=DE=2.???
∴?ABCD的周长=2×(2+5)=14;
故答案为:C.
【分析】根据平行四边形的性质,得到对边平行且相等,得到内错角∠AED=∠BAE,再根据角平分线的性质,得到∠DAE=∠AED,根据等角对等边,得到AD=DE的值,求出?ABCD的周长.
5.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(?? )
A.?4<x<6??????????????????????????B.?2<x<8??????????????????????????C.?0<x<10??????????????????????????D.?0<x<6
【答案】 B
【解析】【解答】解:∵平行四边形ABCD
∴OA=OC=3,OB=OD=5
∴在△AOB中,OB﹣OA<x<OB+OA
即:2<x<8
故选B.
【分析】平行四边形的两条对角线相交于平行四边形的两边构成三角形,这个三角形的两条边是3,5,第三条边就是平行四边形的一条边x,即满足 ,解得即可.
6.如图,如果□ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有(?? )
A.?1对?????????????????????????????????????B.?2对????????????????????????????????????C.?3对?????????????????????????????????????D.?4对
【答案】D
【解析】【解答】∵ABCD是平行四边形,
∴AD=BC,AB=CD,AO=CO,BO=DO.
∵∠AOB=∠COD,∠AOD=∠COB,
∴△ABO≌△CDO,△ADO≌△CBO.
∵BD=BD,AC="AC" ,∴△ABD≌△DCB,△ACD≌△CAB.
∴共有四对.
故答案为:D.
【分析】根据平行四边形的性质及全等三角形的判定方法进行分析,从而得到答案.本题主要考查了平行四边形的性质的运用,记忆平行四边形的性质,应从边、角、对角线三个方面掌握.
7.如图,已知□ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为(????)
A.?6 cm??????????????????????????????????B.?12 cm??????????????????????????????????C.?4 cm??????????????????????????????????D.?8 cm
【答案】 D
【解析】【分析】根据平行四边形的对边相等的性质及三角形的周长公式求解即可.
∵□ABCD的周长是28cm
∴AB+BC=14cm
∵△ABC的周长是22cm,即AB+BC+AC=22cm
∴AC=8cm
故选D.
二、填空题
8.如图,在 ABCD中,∠ODA =90°,AC=10 cm,BD=6cm,则AD的长为________cm.
【答案】 4
【解析】【解答】解:∵四边形ABCD是平行四边形, AC=10 cm,BD=6cm ,
∴OD=BD=3cm,OA=AC=5cm,
在Rt△OAD中,AD2=OA2-OD2=25-9=16,
∴AD=4cm.
故答案为:4.
【分析】根据平行四边形的对角线互相平分,可得OD=BD=3cm,OA=AC=5cm,在Rt△OAD中,利用勾股定理即可求出AD的长.
9.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________.
【答案】 36
【解析】【解答】解:∵四边形ABCD是平行四边形,AB=5,
∴OB=OD=BD,OA=OC=AC,CD=AB=5,
∵△ OCD的周长 =OD+OC+CD=23,
∴OC+OD=18,
即BD+AC=18,
∴BD+AC=36.
故答案为:36.
【分析】根据平行四边形的性质可得OB=OD=BD,OA=OC=AC,CD=AB=5,由△ OCD的周长 =OD+OC+CD=23,可得BD+AC=36,据此求出结论.
10.如图,在平行四边形ABCD中,BC=10,AC=8,BD=14,△AOD的周长是________.
【答案】 21
【解析】【解答】解:∵四边形ABCD是平行四边形
∴AD=BC=10,AO=CO= AC=4,BO=DO= BD=7
∴△AOD的周长=AD+AO+DO=21
故答案为21
【分析】根据平行四边形的对边相等,对角线互相平分得出AD=BC=10,AO=4,OD=7,然后根据三角形周长的计算方法即可算出答案。
三、解答题
11.已知:如图,□ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F,求证:AE=CF.
【答案】证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,
∴∠DAO=∠BCO,
在△AEO和△CFO中,
∵ ,
∴△AEO≌△CFO(ASA),
∴AE=CF.
【解析】【分析】根据平行四边形性质可得AO=CO,AD∥BC,根据平行线性质可得∠DAO=∠BCO,再由全等三角形判定ASA得△AEO≌△CFO,由全等三角形性质即可得证.
12.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE=DF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB.
∵AE=CF,
∴OE=OF.
在△BEO和△DFO中,
,
∴△BEO≌△DFO,
∴BE=DF.
【解析】【分析】根据平行四边形的对角线互相平分得出OA=OC,OD=OB,又AF=CE,根据等量减去等量差相等得出OE=OF,然后利用SAS判断出△BEO≌△DFO,根据全等三角形的对应边相等得出结论,BE=DF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十八章 平行四边形
18.1.1第2课时 平行四边形对角线的特征 同步练习
一、单选题
1.平行四边形所具有的性质是(?? )
A.?对角线相等????????? ??B.?邻边互相垂直??????????
?C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在□ABCD中,E是AB延长线上的一点,若∠1=60°,则∠A的度数为(???).
A.?120°?????????????????????????????????????B.?60°????????????????????????????????C.?45°???????????????????????????????????D.?30°
3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是(?? )
A.?AC⊥BD????????????????????????????B.?AO=OD??????????????????????????
??C.?AC=BD????????????????????????????D.?OA=OC
4.如图,在?ABCD中,AE平分∠DAB,AB=5,DE=2.则?ABCD的周长是(??? )
A.?7?????????????????????????????????????B.?10???????????????????????????????????C.?14????????????????????????????????????????D.?16
5.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(?? )
A.?4<x<6?????????????????????????B.?2<x<8?????????????????????????C.?0<x<10?????????????????????????D.?0<x<6
6.如图,如果□ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有(?? )
A.?1对?????????????????????????????????????B.?2对????????????????????????????????????C.?3对?????????????????????????????????????D.?4对
7.如图,已知□ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为(????)
A.?6 cm??????????????????????????????????B.?12 cm??????????????????????????????????C.?4 cm??????????????????????????????????D.?8 cm
二、填空题
8.如图,在 ABCD中,∠ODA =90°,AC=10 cm,BD=6cm,则AD的长为________cm.
9.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________.
10.如图,在平行四边形ABCD中,BC=10,AC=8,BD=14,△AOD的周长是________.
三、解答题
11.已知:如图,□ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F,求证:AE=CF.
12.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.
参考答案
一、单选题
1.平行四边形所具有的性质是(?? )
A.?对角线相等????????? ??B.?邻边互相垂直??????????
?C.?每条对角线平分一组对角???????????D.?两组对边分别相等
【答案】 D
【解析】【解答】平行四边形的对角相等,对角线互相平分,对边平行且相等.
故答案为:D.
【分析】平行四边形的性质:对边平行且相等,对角线互相平分,对角相等,邻角互补,据此判断即可.
2.在□ABCD中,E是AB延长线上的一点,若∠1=60°,则∠A的度数为(???).
A.?120°?????????????????????????????????????B.?60°????????????????????????????????C.?45°???????????????????????????????????D.?30°
【答案】B
【解析】
【分析】根据平行四边形的性质:平行四边形的对边平行.由?ABCD可知AD∥BC,所以
∠1=∠A=60°.
【解答】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠A=60°.
故选:B.
3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是(?? )
A.?AC⊥BD????????????????????????????B.?AO=OD??????????????????????????
??C.?AC=BD????????????????????????????D.?OA=OC
【答案】D
【解析】【解答】A、菱形的对角线才相互垂直,A不符合题意;
B、平行四边形中,AO不一定等于OD,B不符合题意;
C、只有平行四边形为矩形时,其对角线相等,C不符合题意;
D、平行四边形对角线互相平分,D符合题意;.
故答案为:D.
【分析】根据平行四边形的性质判断.平行四边形的对角线互相平分.
4.如图,在?ABCD中,AE平分∠DAB,AB=5,DE=2.则?ABCD的周长是(??? )
A.?7??????????????????????????????????????B.?10????????????????????????????????????C.?14?????????????????????????????????????????D.?16
【答案】C
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=5,AB∥CD,BC=AD,
∴∠AED=∠BAE,
又∵AE平分∠DAB,
∴∠DAE=∠BAE.
∴∠DAE=∠AED.
∴AD=DE=2.???
∴?ABCD的周长=2×(2+5)=14;
故答案为:C.
【分析】根据平行四边形的性质,得到对边平行且相等,得到内错角∠AED=∠BAE,再根据角平分线的性质,得到∠DAE=∠AED,根据等角对等边,得到AD=DE的值,求出?ABCD的周长.
5.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(?? )
A.?4<x<6??????????????????????????B.?2<x<8??????????????????????????C.?0<x<10??????????????????????????D.?0<x<6
【答案】 B
【解析】【解答】解:∵平行四边形ABCD
∴OA=OC=3,OB=OD=5
∴在△AOB中,OB﹣OA<x<OB+OA
即:2<x<8
故选B.
【分析】平行四边形的两条对角线相交于平行四边形的两边构成三角形,这个三角形的两条边是3,5,第三条边就是平行四边形的一条边x,即满足 ,解得即可.
6.如图,如果□ABCD的对角线AC,BD相交于点O,那么图中的全等三角形共有(?? )
A.?1对?????????????????????????????????????B.?2对????????????????????????????????????C.?3对?????????????????????????????????????D.?4对
【答案】D
【解析】【解答】∵ABCD是平行四边形,
∴AD=BC,AB=CD,AO=CO,BO=DO.
∵∠AOB=∠COD,∠AOD=∠COB,
∴△ABO≌△CDO,△ADO≌△CBO.
∵BD=BD,AC="AC" ,∴△ABD≌△DCB,△ACD≌△CAB.
∴共有四对.
故答案为:D.
【分析】根据平行四边形的性质及全等三角形的判定方法进行分析,从而得到答案.本题主要考查了平行四边形的性质的运用,记忆平行四边形的性质,应从边、角、对角线三个方面掌握.
7.如图,已知□ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为(????)
A.?6 cm??????????????????????????????????B.?12 cm??????????????????????????????????C.?4 cm??????????????????????????????????D.?8 cm
【答案】 D
【解析】【分析】根据平行四边形的对边相等的性质及三角形的周长公式求解即可.
∵□ABCD的周长是28cm
∴AB+BC=14cm
∵△ABC的周长是22cm,即AB+BC+AC=22cm
∴AC=8cm
故选D.
二、填空题
8.如图,在 ABCD中,∠ODA =90°,AC=10 cm,BD=6cm,则AD的长为________cm.
【答案】 4
【解析】【解答】解:∵四边形ABCD是平行四边形, AC=10 cm,BD=6cm ,
∴OD=BD=3cm,OA=AC=5cm,
在Rt△OAD中,AD2=OA2-OD2=25-9=16,
∴AD=4cm.
故答案为:4.
【分析】根据平行四边形的对角线互相平分,可得OD=BD=3cm,OA=AC=5cm,在Rt△OAD中,利用勾股定理即可求出AD的长.
9.如图, ABCD的对角线交于点O,且AB=5, OCD的周长为23,则 ABCD的两条对角线长的和是________.
【答案】 36
【解析】【解答】解:∵四边形ABCD是平行四边形,AB=5,
∴OB=OD=BD,OA=OC=AC,CD=AB=5,
∵△ OCD的周长 =OD+OC+CD=23,
∴OC+OD=18,
即BD+AC=18,
∴BD+AC=36.
故答案为:36.
【分析】根据平行四边形的性质可得OB=OD=BD,OA=OC=AC,CD=AB=5,由△ OCD的周长 =OD+OC+CD=23,可得BD+AC=36,据此求出结论.
10.如图,在平行四边形ABCD中,BC=10,AC=8,BD=14,△AOD的周长是________.
【答案】 21
【解析】【解答】解:∵四边形ABCD是平行四边形
∴AD=BC=10,AO=CO= AC=4,BO=DO= BD=7
∴△AOD的周长=AD+AO+DO=21
故答案为21
【分析】根据平行四边形的对边相等,对角线互相平分得出AD=BC=10,AO=4,OD=7,然后根据三角形周长的计算方法即可算出答案。
三、解答题
11.已知:如图,□ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F,求证:AE=CF.
【答案】证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,
∴∠DAO=∠BCO,
在△AEO和△CFO中,
∵ ,
∴△AEO≌△CFO(ASA),
∴AE=CF.
【解析】【分析】根据平行四边形性质可得AO=CO,AD∥BC,根据平行线性质可得∠DAO=∠BCO,再由全等三角形判定ASA得△AEO≌△CFO,由全等三角形性质即可得证.
12.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE=DF.
【答案】
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB.
∵AE=CF,
∴OE=OF.
在△BEO和△DFO中,
,
∴△BEO≌△DFO,
∴BE=DF.
【解析】【分析】根据平行四边形的对角线互相平分得出OA=OC,OD=OB,又AF=CE,根据等量减去等量差相等得出OE=OF,然后利用SAS判断出△BEO≌△DFO,根据全等三角形的对应边相等得出结论,BE=DF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
