18.1.2 第3课时三角形的中位线同步练习(附答案)
文档属性
| 名称 | 18.1.2 第3课时三角形的中位线同步练习(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十八章 平行四边形
18.1.2第3课时 三角形的中位线 同步练习
一、单选题(共7题;共14分)
1.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是(? )
A.?DE是△BCD的中线?????????B.?BD是△ABC的中线?????????
C.?AD=DC,BE=EC???????? ?D.?AD=EC,DC=BE
2.如图,在一次实践活动课上,小刚为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 ,然后测量出 , 的中点 , ,且 ,于是可以计算出池塘 , 两点间的距离是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
3.如图,DE是△ABC的中位线,若BC的长是3cm,则DE的长是
A.?2cm???????????????????????????????????B.?1.5cm???????????????????????????????????C.?1.2cm???????????????????????????????????D.?1cm
4.如图,要测量被池塘隔开的A,B两点的距离,小明在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE,现测得DE=45米,那么AB等于(??? )
A.?90米??????????????????????????????????B.?88米??????????????????????????????????C.?86米??????????????????????????????????D.?84米
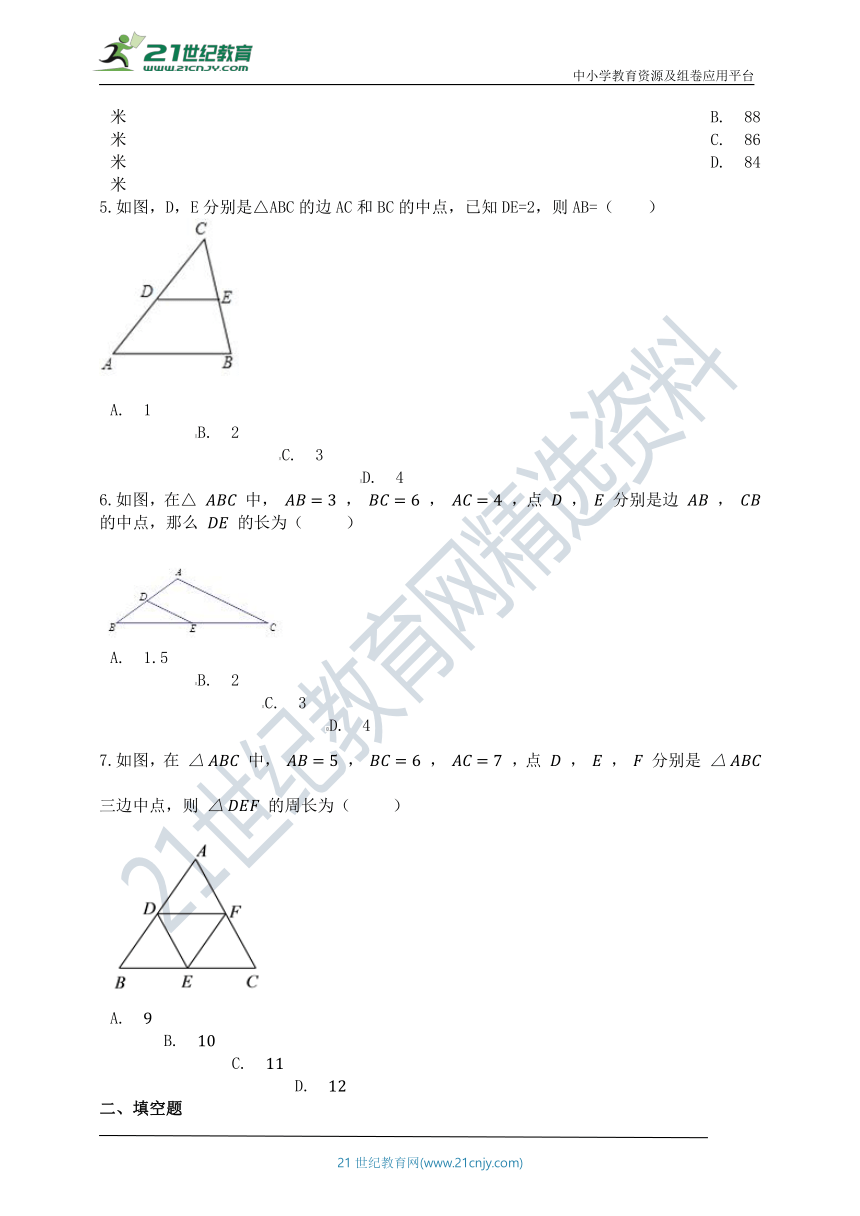
5.如图,D,E分别是△ABC的边AC和BC的中点,已知DE=2,则AB=( )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?3?????????????????????????????????????????D.?4
6.如图,在△ 中, , , ,点 , 分别是边 , 的中点,那么 的长为(?? )
A.?1.5????????????????????????????????????????B.?2????????????????????????????????????????C.?3????????????????????????????????????????D.?4
7.如图,在 中, , , ,点 , , 分别是 三边中点,则 的周长为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
二、填空题
8.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是3,则AC的长为________.
9.如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: ________ (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而________(填“不变”或“改变”).
10.已知△ABC的3条中位线分别为 3 cm、4 cm、5 cm,则△ABC的周长为________cm.
11.若三角形各边长分别为8cm、10cm、16cm,则以各边中点为顶点的三角形的周长是________.
12.如图,△ABC中,D,E分别 是边AB,AC的中点.若DE=2,则BC=________.
三、解答题(共2题;共10分)
13.如图,在?ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF= BC,求证:四边形OCFE是平行四边形.
14.如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:∵D、E分别是△ABC的边AC、BC的中点,
∴DE是△BCD的中线,BD是△ABC的中线,AD=DC,BE=EC.
但不能得到AD=EC和DC=BE.
故答案为:D.
【分析】连接三角形一边中点与这边所对的顶点的线段就是三角形的中线;连接三角形两边中点的线段就是三角形的中位线;根据定义即可一一判断得出答案。
2.【答案】 D
【解析】【解答】∵点 、 是 中 、 边上中点,
∴ ,
∵ ,
∴ .
故答案为:D.
【分析】利用三角形中位线定义和三角形中位线定理便可计算出B、C两点的距离应是选项D
3.【答案】 B
【解析】【分析】三角形中位线的性质:三角形的中位线平行于第三边,且等于第三边的一半;本题利用定理计算即可.
∵DE是△ABC的中位线,
∴DE=? BC,
∵BC的长为3cm,
∴DE=1.5.
故选B.
4.【答案】 A
【解析】【解答】解:∵点D、E分别是AC、BC的中点
∴AB=2DE=2×45=90(米).
故答案为:A.
【分析】根据三角形的中位线定理易求AB的长。
5.【答案】 D
【解析】
【分析】根据三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半可知,ED=AB,进而由DE的值求得AB.
【解答】∵D,E分别是△ABC的边AC和BC的中点,
∴DE是△ABC的中位线,
∵DE=2,
∴AB=2DE=4.
故选D.
【点评】本题主要考查三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.
6.【答案】 B
【解析】【解答】解:∵点 , 分别是边 , 的中点,
?.故选B.
7.【答案】 A
【解析】【解答】∵ , , 分别是 三边中点,
∴ , , 为 中位线,
∴ , , .
∵ , , ,
∴ , , ,
∴ ,
故答案为: .
【分析】由三角形中位线性质,可得结果。
二、填空题
8.【答案】 6
【解析】【解答】解:∵点D,E分别是边AB,BC的中点,
∴AC=2DE=6。
故答案为:6。
【分析】根据三角形的中位线等于第三边的一半即可算出AC的长。
9.【答案】=;不变
【解析】【解答】过 作 , ,
∵ 是 与 的中位线,
∴ ,
∴ ,
故答案为: .
随横板的长度的变化而不变.故答案为:? (1). =??? (2). 不变.
【分析】过 B 作 B D ⊥ A D , B ′ D ′ ⊥ A ′ D ′ ,由题意知O C 是 △ A B D 与 △ A ′ B ′ D ′ 的中位线,所以根据三角形的中位线定理可得BD=B′D′=2OC,则可得h1=h2,即h 随横板的长度的变化而不变。
10.【答案】24
【解析】【解答】∵三角形的3条中位线分别为3cm、4cm、5cm,
根据三角形的中位线定理,得三角形的三边分别是6cm、8cm、10cm,
则三角形的周长是24cm.
【分析】因为△ABC的3条中位线分别为 3 cm、4 cm、5 cm,所以根据三角形的中位线定理可得△ABC的三边长分别为6cm、8cm、10cm,则△ABC的周长为三边之和。
11.【答案】 17cm
【解析】【解答】如图,D,E,F分别是△ABC的三边的中点,
则DE= AC,DF= BC,EF= AB,
∴△DEF的周长=DE+DF+EF= (AC+BC+AB)= ×(8+10+16)cm=17cm,
故答案为:17cm.
【分析】 根据三角形中位线等于第三边的一半求出以各边中点为顶点的三角形的各边长,根据周长公式计算,得到答案.
12.【答案】 4
【解析】【解答】∵△ABC中,D、E分别是△ABC的边AB、AC的中点,DE=2
∴DE是△ABC的中位线,
∴BC=2DE=2×2=4.
【分析】根据三角形的中位线等于第三边的一半即可求解.
三、解答题
13.【答案】证明:∴OE∥BC,且OE= BC. 又∵CF= BC,∴OE=CF. 又∵点F在BC的延长线上,∴OE∥CF,∴四边形OCFE是平行四边形
【解析】【分析】根据已知条件可得OE是三角形BCD的中位线,所以由三角形中位线定理可得OE= BC,OEBC,结合已知条件可得OE=CF,根据一组对边平行且相等的四边形是平行四边形可得四边形OCFE是平行四边形.
14.【答案】(1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵EF∥AB,
∴四边形DBFE是平行四边形;
(2)解:当AB=BC时,四边形DBFE是菱形.
理由如下:∵D是AB的中点,
∴BD=AB,
∵DE是△ABC的中位线,
∴DE=BC,
∵AB=BC,
∴BD=DE,
又∵四边形DBFE是平行四边形,
∴四边形DBFE是菱形.
【解析】【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明;
(2)根据邻边相等的平行四边形是菱形证明.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十八章 平行四边形
18.1.2第3课时 三角形的中位线 同步练习
一、单选题(共7题;共14分)
1.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是(? )
A.?DE是△BCD的中线?????????B.?BD是△ABC的中线?????????
C.?AD=DC,BE=EC???????? ?D.?AD=EC,DC=BE
2.如图,在一次实践活动课上,小刚为了测量池塘 , 两点间的距离,他先在池塘的一侧选定一点 ,然后测量出 , 的中点 , ,且 ,于是可以计算出池塘 , 两点间的距离是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
3.如图,DE是△ABC的中位线,若BC的长是3cm,则DE的长是
A.?2cm???????????????????????????????????B.?1.5cm???????????????????????????????????C.?1.2cm???????????????????????????????????D.?1cm
4.如图,要测量被池塘隔开的A,B两点的距离,小明在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE,现测得DE=45米,那么AB等于(??? )
A.?90米??????????????????????????????????B.?88米??????????????????????????????????C.?86米??????????????????????????????????D.?84米
5.如图,D,E分别是△ABC的边AC和BC的中点,已知DE=2,则AB=( )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?3?????????????????????????????????????????D.?4
6.如图,在△ 中, , , ,点 , 分别是边 , 的中点,那么 的长为(?? )
A.?1.5????????????????????????????????????????B.?2????????????????????????????????????????C.?3????????????????????????????????????????D.?4
7.如图,在 中, , , ,点 , , 分别是 三边中点,则 的周长为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
二、填空题
8.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是3,则AC的长为________.
9.如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: ________ (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而________(填“不变”或“改变”).
10.已知△ABC的3条中位线分别为 3 cm、4 cm、5 cm,则△ABC的周长为________cm.
11.若三角形各边长分别为8cm、10cm、16cm,则以各边中点为顶点的三角形的周长是________.
12.如图,△ABC中,D,E分别 是边AB,AC的中点.若DE=2,则BC=________.
三、解答题(共2题;共10分)
13.如图,在?ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF= BC,求证:四边形OCFE是平行四边形.
14.如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:∵D、E分别是△ABC的边AC、BC的中点,
∴DE是△BCD的中线,BD是△ABC的中线,AD=DC,BE=EC.
但不能得到AD=EC和DC=BE.
故答案为:D.
【分析】连接三角形一边中点与这边所对的顶点的线段就是三角形的中线;连接三角形两边中点的线段就是三角形的中位线;根据定义即可一一判断得出答案。
2.【答案】 D
【解析】【解答】∵点 、 是 中 、 边上中点,
∴ ,
∵ ,
∴ .
故答案为:D.
【分析】利用三角形中位线定义和三角形中位线定理便可计算出B、C两点的距离应是选项D
3.【答案】 B
【解析】【分析】三角形中位线的性质:三角形的中位线平行于第三边,且等于第三边的一半;本题利用定理计算即可.
∵DE是△ABC的中位线,
∴DE=? BC,
∵BC的长为3cm,
∴DE=1.5.
故选B.
4.【答案】 A
【解析】【解答】解:∵点D、E分别是AC、BC的中点
∴AB=2DE=2×45=90(米).
故答案为:A.
【分析】根据三角形的中位线定理易求AB的长。
5.【答案】 D
【解析】
【分析】根据三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半可知,ED=AB,进而由DE的值求得AB.
【解答】∵D,E分别是△ABC的边AC和BC的中点,
∴DE是△ABC的中位线,
∵DE=2,
∴AB=2DE=4.
故选D.
【点评】本题主要考查三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.
6.【答案】 B
【解析】【解答】解:∵点 , 分别是边 , 的中点,
?.故选B.
7.【答案】 A
【解析】【解答】∵ , , 分别是 三边中点,
∴ , , 为 中位线,
∴ , , .
∵ , , ,
∴ , , ,
∴ ,
故答案为: .
【分析】由三角形中位线性质,可得结果。
二、填空题
8.【答案】 6
【解析】【解答】解:∵点D,E分别是边AB,BC的中点,
∴AC=2DE=6。
故答案为:6。
【分析】根据三角形的中位线等于第三边的一半即可算出AC的长。
9.【答案】=;不变
【解析】【解答】过 作 , ,
∵ 是 与 的中位线,
∴ ,
∴ ,
故答案为: .
随横板的长度的变化而不变.故答案为:? (1). =??? (2). 不变.
【分析】过 B 作 B D ⊥ A D , B ′ D ′ ⊥ A ′ D ′ ,由题意知O C 是 △ A B D 与 △ A ′ B ′ D ′ 的中位线,所以根据三角形的中位线定理可得BD=B′D′=2OC,则可得h1=h2,即h 随横板的长度的变化而不变。
10.【答案】24
【解析】【解答】∵三角形的3条中位线分别为3cm、4cm、5cm,
根据三角形的中位线定理,得三角形的三边分别是6cm、8cm、10cm,
则三角形的周长是24cm.
【分析】因为△ABC的3条中位线分别为 3 cm、4 cm、5 cm,所以根据三角形的中位线定理可得△ABC的三边长分别为6cm、8cm、10cm,则△ABC的周长为三边之和。
11.【答案】 17cm
【解析】【解答】如图,D,E,F分别是△ABC的三边的中点,
则DE= AC,DF= BC,EF= AB,
∴△DEF的周长=DE+DF+EF= (AC+BC+AB)= ×(8+10+16)cm=17cm,
故答案为:17cm.
【分析】 根据三角形中位线等于第三边的一半求出以各边中点为顶点的三角形的各边长,根据周长公式计算,得到答案.
12.【答案】 4
【解析】【解答】∵△ABC中,D、E分别是△ABC的边AB、AC的中点,DE=2
∴DE是△ABC的中位线,
∴BC=2DE=2×2=4.
【分析】根据三角形的中位线等于第三边的一半即可求解.
三、解答题
13.【答案】证明:∴OE∥BC,且OE= BC. 又∵CF= BC,∴OE=CF. 又∵点F在BC的延长线上,∴OE∥CF,∴四边形OCFE是平行四边形
【解析】【分析】根据已知条件可得OE是三角形BCD的中位线,所以由三角形中位线定理可得OE= BC,OEBC,结合已知条件可得OE=CF,根据一组对边平行且相等的四边形是平行四边形可得四边形OCFE是平行四边形.
14.【答案】(1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵EF∥AB,
∴四边形DBFE是平行四边形;
(2)解:当AB=BC时,四边形DBFE是菱形.
理由如下:∵D是AB的中点,
∴BD=AB,
∵DE是△ABC的中位线,
∴DE=BC,
∵AB=BC,
∴BD=DE,
又∵四边形DBFE是平行四边形,
∴四边形DBFE是菱形.
【解析】【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明;
(2)根据邻边相等的平行四边形是菱形证明.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
