必修5 1.1正弦定理 课件(共37张PPT)
文档属性
| 名称 | 必修5 1.1正弦定理 课件(共37张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
1.1.1 正弦定理
1、边的关系:
2、角的关系:
3、边角关系:
1)两边之和大于第三边;两边之差小于第三边
2)在直角三角形中:a2+b2=c2
1)A+B+C=1800
1)大边对大角,大角对大边,等边对等角
2)在直角三角形ABC中,C=900,则
回顾三角形中的边角关系:
一、前提测评
教学目标:
(1)掌握正弦定理的推导
(2)理解正弦定理在解三角形中的作用;
(3)能运用正弦定理解三角形;
(4)通过讨论和探究,使学生形成探索问题的习惯;
重难点:运用正弦定理解三角形;
教学方法:探究法
对任意三角形,这个等式都会成立吗?
怎么证明这个结论?
在直角三角形中:
正弦定理的发现
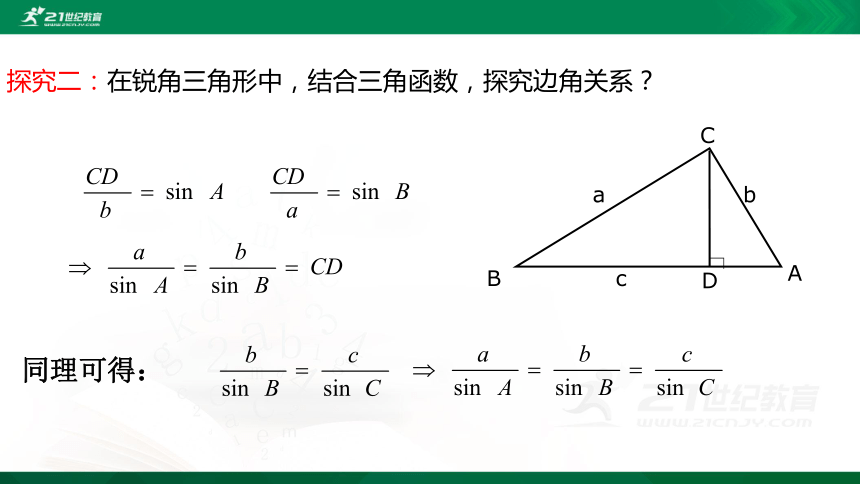
探究二:在锐角三角形中,结合三角函数,探究边角关系?
A
C
B
b
a
c
D
同理可得:
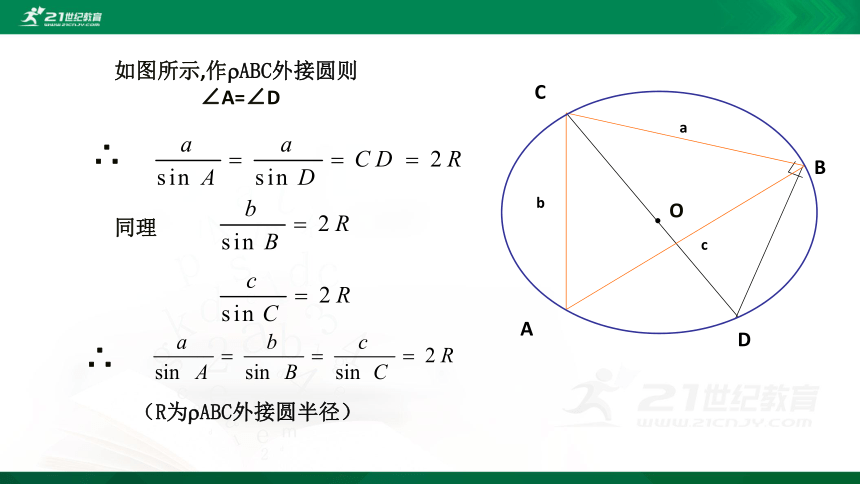
如图所示,作?ABC外接圆则
∴
同理
∴
(R为?ABC外接圆半径)
A
B
C
a
b
c
O
D
∠A=∠D
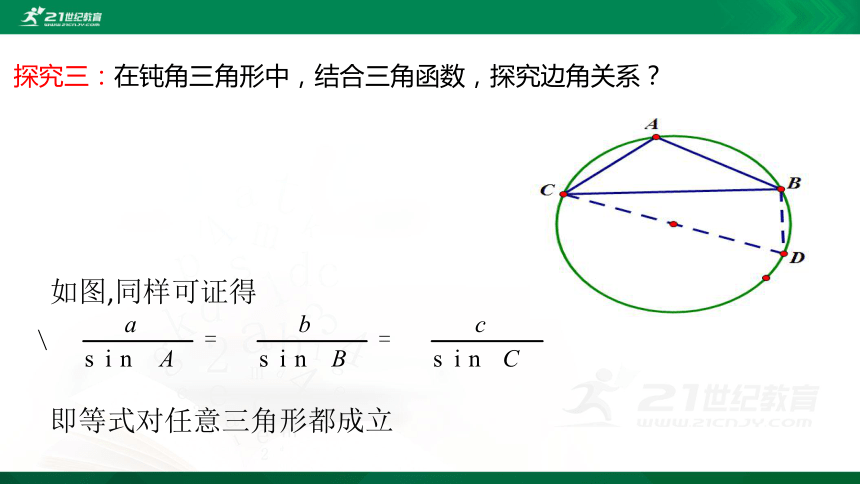
探究三:在钝角三角形中,结合三角函数,探究边角关系?
如图,同样可证得
即等式对任意三角形都成立
正弦定理
在任意一个三角形中,各边和它所对角的正弦的比相等,即
注意:定理适合任意三角形。
A
B
C
a
c
b
(2R是三角形外接圆的直径)
证法二:(面积法)
在任意斜?ABC当中
作AD⊥BC于D
∴
∵
∴
同理可证
D
A
B
C
c
a
b
h
(一)正弦定理的证明
1、当?ABC为锐角三角形时,如图(1)
证明:
过A作单位向量 垂直,
则 的夹角为________,
的夹角为________,
的夹角为________.
已知:?ABC中,CB=a,AC=b,AB=c.
求证:
A
C
B
a
b
c
j
方法三(向量法)
A
C
B
a
b
c
正弦定理
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即:
变形应用:
a : b : c = sinA : sinB : sinC
asinB=bsinA csinB=bsinc csinA=asinB
小结与思考
问题 通过以上的研究过程,同学们主要学到了那些知识和方法?你对此有何体会?
1. 用向量证明了正弦定理,体现了数形结合的 数学思想
2. 它表述了三角形的边与对角的正弦值的关系.
3. 定理证明分别从直角、锐角、钝角出发,运 用分类讨论的思想.
一般性结论:把三角形的三个角A,B,C和三条边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。
知识回顾:应用正弦定理解三角形需要几个元素?什么样的元素?
正弦定理在解斜三角形中的两类应用:
(1)、已知两角和任一边,求一角和其他两条边.
(2)、已知两边和其中一边的对角,求另一边的对角(进而求其他的角和边)
A
B
a
C
A
a
a
b
B
例题分析与点评:
例1:在△ABC中,已知A=32.00,B=81.80,a=42.9cm,解三角形.
(一)思路:
(二)点评:
(三)规范答题:
A
C
B
b
a
c
解:∵A+B+C=1800 ∴C=1800-(A+B)
=1800-(32.00+81.80)=66.20
根据正弦定理,
根据正弦定理,
例2:在△ABC中,已知a=20cm,b=28cm,A=400,解三角形(角度精确到10,边长精确到1cm).
(一)思路:
(二)点评:
(三)规范答题:
A
C
B
b
a
c
解:根据正弦定理,
∴B≈640
错!
∵00∴B≈640或B≈1160
(1)当B≈640时,…
(2)当B≈1160时,…
特别注意!
变例一:在△ABC中,已知a=20cm,b= cm,A=600,解三角形(角度精确到10,边长精确到1cm).
解:根据正弦定理,
∵00∴B=300或B=1500
(正确解法)解:根据正弦定理,
∵00b
∴B=300
……
变例二:在△ABC中,已知a=22cm,b=25cm cm,A=1330,解三角形(角度精确到0.010,边长精确到1cm).
解:根据正弦定理,
∵00∴B≈56.210或B≈123.790
∴B≈56.210或B≈123.790
(正确解法)解:根据正弦定理,
∵00而A=1330
∴这样的三角形不存在!
例3、ΔABC中,c= ,A=450 a=2,
求b和B、C
解:∵ =
∴ sinC= =sinC= =
b= = = +1
∴C=600
∴当C=600时,B=750
或C=1200
24
∴当C=1200 时,B=150 ,
b= = = -1
∴b= +1, B=750 ,C=600
或b= -1, B=150 ,C=1200
25
例2、在ΔABC中,b= ,B=600 ,c=1,求a和A,C
解:∵ =
∴ sinC= = =
∴ B=900 a= =2
∵b>c,B=600 ∴C∴C=300
若A为锐角时:
若A为直角或钝角时:
已知a,b和A,用正弦定理求B时的各种情况:
判断满足下列的三角形的个数:
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o
两解
一解
两解
无解
练习:
四、反馈练习
1、根据下列条件确定△ABC有两个解的是( )
A.a=18 B=300 A=1200
B.a=60 c=48 C=1200
C.a=3 b=6 A=300
D.a=14 b=15 A=450
2、根据下列条件解三角形
(1)已知在△ABC中a=8,B=600,C=450,求b
(2)已知在△ABC中b= ,c=1,B=450, 求C
由正弦定理可得:
由正弦定理可得:
答案:
1、由正弦定理可得:
A:
B:由于a>c,故A>C,无解
C:
D:
四、当堂训练
1、在 中,已知下列条件,解三角形(角度精确到1度,边长精确到1cm):
(1)
(2)
例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B
解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050
由 = 得 a= = =10
由 =
得 b= = = 20sin750=20×
= 5 +5
例题讲解:
2、在 中,已知下列条件,解三角形(角度精确到1度,边长精确到1cm):
(1)
(2)
小结:
(1)正弦定理的熟记方法
(2)利用正弦定理可以用于两类解三角形的问题。一是已知任意两角与一边;二是已知二边与其中一边的对角;
(3)利用正弦定理求角时要注意大边对大角,解的个数,避免漏角。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.1.1 正弦定理
1、边的关系:
2、角的关系:
3、边角关系:
1)两边之和大于第三边;两边之差小于第三边
2)在直角三角形中:a2+b2=c2
1)A+B+C=1800
1)大边对大角,大角对大边,等边对等角
2)在直角三角形ABC中,C=900,则
回顾三角形中的边角关系:
一、前提测评
教学目标:
(1)掌握正弦定理的推导
(2)理解正弦定理在解三角形中的作用;
(3)能运用正弦定理解三角形;
(4)通过讨论和探究,使学生形成探索问题的习惯;
重难点:运用正弦定理解三角形;
教学方法:探究法
对任意三角形,这个等式都会成立吗?
怎么证明这个结论?
在直角三角形中:
正弦定理的发现
探究二:在锐角三角形中,结合三角函数,探究边角关系?
A
C
B
b
a
c
D
同理可得:
如图所示,作?ABC外接圆则
∴
同理
∴
(R为?ABC外接圆半径)
A
B
C
a
b
c
O
D
∠A=∠D
探究三:在钝角三角形中,结合三角函数,探究边角关系?
如图,同样可证得
即等式对任意三角形都成立
正弦定理
在任意一个三角形中,各边和它所对角的正弦的比相等,即
注意:定理适合任意三角形。
A
B
C
a
c
b
(2R是三角形外接圆的直径)
证法二:(面积法)
在任意斜?ABC当中
作AD⊥BC于D
∴
∵
∴
同理可证
D
A
B
C
c
a
b
h
(一)正弦定理的证明
1、当?ABC为锐角三角形时,如图(1)
证明:
过A作单位向量 垂直,
则 的夹角为________,
的夹角为________,
的夹角为________.
已知:?ABC中,CB=a,AC=b,AB=c.
求证:
A
C
B
a
b
c
j
方法三(向量法)
A
C
B
a
b
c
正弦定理
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即:
变形应用:
a : b : c = sinA : sinB : sinC
asinB=bsinA csinB=bsinc csinA=asinB
小结与思考
问题 通过以上的研究过程,同学们主要学到了那些知识和方法?你对此有何体会?
1. 用向量证明了正弦定理,体现了数形结合的 数学思想
2. 它表述了三角形的边与对角的正弦值的关系.
3. 定理证明分别从直角、锐角、钝角出发,运 用分类讨论的思想.
一般性结论:把三角形的三个角A,B,C和三条边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。
知识回顾:应用正弦定理解三角形需要几个元素?什么样的元素?
正弦定理在解斜三角形中的两类应用:
(1)、已知两角和任一边,求一角和其他两条边.
(2)、已知两边和其中一边的对角,求另一边的对角(进而求其他的角和边)
A
B
a
C
A
a
a
b
B
例题分析与点评:
例1:在△ABC中,已知A=32.00,B=81.80,a=42.9cm,解三角形.
(一)思路:
(二)点评:
(三)规范答题:
A
C
B
b
a
c
解:∵A+B+C=1800 ∴C=1800-(A+B)
=1800-(32.00+81.80)=66.20
根据正弦定理,
根据正弦定理,
例2:在△ABC中,已知a=20cm,b=28cm,A=400,解三角形(角度精确到10,边长精确到1cm).
(一)思路:
(二)点评:
(三)规范答题:
A
C
B
b
a
c
解:根据正弦定理,
∴B≈640
错!
∵00
(1)当B≈640时,…
(2)当B≈1160时,…
特别注意!
变例一:在△ABC中,已知a=20cm,b= cm,A=600,解三角形(角度精确到10,边长精确到1cm).
解:根据正弦定理,
∵00
(正确解法)解:根据正弦定理,
∵00
∴B=300
……
变例二:在△ABC中,已知a=22cm,b=25cm cm,A=1330,解三角形(角度精确到0.010,边长精确到1cm).
解:根据正弦定理,
∵00
∴B≈56.210或B≈123.790
(正确解法)解:根据正弦定理,
∵00
∴这样的三角形不存在!
例3、ΔABC中,c= ,A=450 a=2,
求b和B、C
解:∵ =
∴ sinC= =sinC= =
b= = = +1
∴C=600
∴当C=600时,B=750
或C=1200
24
∴当C=1200 时,B=150 ,
b= = = -1
∴b= +1, B=750 ,C=600
或b= -1, B=150 ,C=1200
25
例2、在ΔABC中,b= ,B=600 ,c=1,求a和A,C
解:∵ =
∴ sinC= = =
∴ B=900 a= =2
∵b>c,B=600 ∴C
若A为锐角时:
若A为直角或钝角时:
已知a,b和A,用正弦定理求B时的各种情况:
判断满足下列的三角形的个数:
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o
两解
一解
两解
无解
练习:
四、反馈练习
1、根据下列条件确定△ABC有两个解的是( )
A.a=18 B=300 A=1200
B.a=60 c=48 C=1200
C.a=3 b=6 A=300
D.a=14 b=15 A=450
2、根据下列条件解三角形
(1)已知在△ABC中a=8,B=600,C=450,求b
(2)已知在△ABC中b= ,c=1,B=450, 求C
由正弦定理可得:
由正弦定理可得:
答案:
1、由正弦定理可得:
A:
B:由于a>c,故A>C,无解
C:
D:
四、当堂训练
1、在 中,已知下列条件,解三角形(角度精确到1度,边长精确到1cm):
(1)
(2)
例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B
解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050
由 = 得 a= = =10
由 =
得 b= = = 20sin750=20×
= 5 +5
例题讲解:
2、在 中,已知下列条件,解三角形(角度精确到1度,边长精确到1cm):
(1)
(2)
小结:
(1)正弦定理的熟记方法
(2)利用正弦定理可以用于两类解三角形的问题。一是已知任意两角与一边;二是已知二边与其中一边的对角;
(3)利用正弦定理求角时要注意大边对大角,解的个数,避免漏角。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
