人教版九年级下册 28.1 :锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 人教版九年级下册 28.1 :锐角三角函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 23:13:57 | ||
图片预览



文档简介
锐角三角函数 同步练习
一、选择题
1、在Rt△ABC中,各边都扩大5倍,则角A的三角函数值(?? )
A.不变??? B.扩大5倍?? ? C.缩小5倍?? ? D.不能确定
2、2cos30°的值等于( )
A.1??????? B.??????? C.?????? D.2
3、在Rt△ABC中,∠C=90°,BC=3,AB=5,则sinA的值为( )
A. ??????B.? ????????C.? ???????D.以上都不对
4、如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin的值是(?? )
A.?????? B.??????? C.??????? D. ??????????????????????
5、在△ABC中,∠C=90°.若AB=3,BC=1,则sinA的值为( )
A.??? B.????? ? C.???? ? D.3
6、在菱形ABCD中,BD为对角线,AB=BD,则sin∠BAD=( )
A.?????? B.??????? C.???????? D.
7、如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,下列线段的比值等于cosA的值的有( )个
(1)??? (2)??? (3)??? (4).
A.1???? B.2???? C.3???? D.4
8、=( )
A.????? B.? C.? D.1
9、在△ABC中,∠C=90°,,则sinB的值是(? ?)
A.?????? B.?????? C. ???????D.
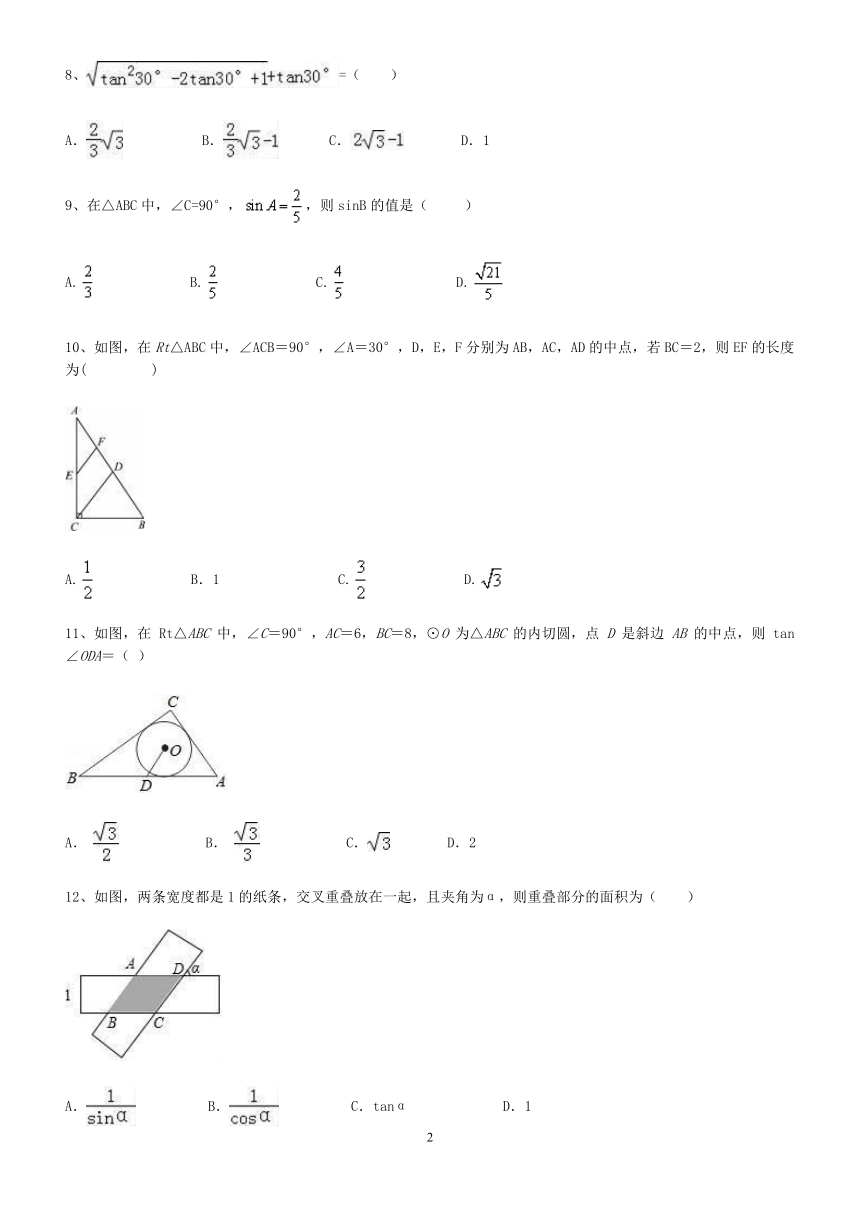
10、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为(???? )
A.? ?????B.1 C.? ?????D.
11、如图,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,⊙O 为△ABC 的内切圆,点 D 是斜边 AB 的中点,则 tan∠ODA=( )
A. ??????B. ??????C.?? D.2
12、如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
A.? ? B.?? C.tanα?????? D.1
二、填空题
13、计算;sin30°?tan30°+cos60°?tan60°= ???? .
14、△ABC中,∠A、∠B都是锐角,且sinA=cosB=,则△ABC是 ?? 三角形.
15、△ABC中,∠A,∠B都是锐角,若sinA=,cosB=,则∠C= .
16、如果3sinα=+1,则∠α= ?? .(精确到0.1度)
17、已知在Rt△ABC中,∠C=90°,sin A=,则tan B的值为 .
18、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tanA+tanB的值为 ??? .
三、简答题
19、在Rt△ABC中,∠C=90°,BC∶AC=3∶4,求∠A的三个三角函数值.
20、设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件求∠B的三个三角函数值:(自己画图)
(1)a=1,b=2;??????? (2)a=5,c=13.
21、先化简,再求代数式(+)÷的值,其中x=sin60°﹣cos45°
22、先化简,再求值:(﹣)÷,其中x=2sin30°+2cos45°.
23、如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠ADE的正弦值.
24、小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(1)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
参考答案
一、选择题
1、A;2、C.;3、A;4、C;5、A;6、C;7、C;8、D.;9、D;10、B;11、D.;12、A;
二、填空题
13、
14、 直角
15、60°? ? ???
16、65.5°
17、.
18、3
三、简答题
19、
20、
21、解:原式=(﹣)?
=?
=
=,
当x=sin60°﹣cos45°=×﹣×=时,
原式==﹣17.
22、:原式=÷
=×
=
∵x=2sin30°+2cos45°
=2×+2×=3,
∴原式=.
23、解:(1)CD与⊙O相切.
理由是:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切.
(2)连接BE,由圆周角定理,得∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×3=6(cm).
在Rt△ABE中,
sin∠ABE==,
∴sin∠ADE=sin∠ABE=.
24、解1:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
一、选择题
1、在Rt△ABC中,各边都扩大5倍,则角A的三角函数值(?? )
A.不变??? B.扩大5倍?? ? C.缩小5倍?? ? D.不能确定
2、2cos30°的值等于( )
A.1??????? B.??????? C.?????? D.2
3、在Rt△ABC中,∠C=90°,BC=3,AB=5,则sinA的值为( )
A. ??????B.? ????????C.? ???????D.以上都不对
4、如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin的值是(?? )
A.?????? B.??????? C.??????? D. ??????????????????????
5、在△ABC中,∠C=90°.若AB=3,BC=1,则sinA的值为( )
A.??? B.????? ? C.???? ? D.3
6、在菱形ABCD中,BD为对角线,AB=BD,则sin∠BAD=( )
A.?????? B.??????? C.???????? D.
7、如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,下列线段的比值等于cosA的值的有( )个
(1)??? (2)??? (3)??? (4).
A.1???? B.2???? C.3???? D.4
8、=( )
A.????? B.? C.? D.1
9、在△ABC中,∠C=90°,,则sinB的值是(? ?)
A.?????? B.?????? C. ???????D.
10、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为(???? )
A.? ?????B.1 C.? ?????D.
11、如图,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,⊙O 为△ABC 的内切圆,点 D 是斜边 AB 的中点,则 tan∠ODA=( )
A. ??????B. ??????C.?? D.2
12、如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
A.? ? B.?? C.tanα?????? D.1
二、填空题
13、计算;sin30°?tan30°+cos60°?tan60°= ???? .
14、△ABC中,∠A、∠B都是锐角,且sinA=cosB=,则△ABC是 ?? 三角形.
15、△ABC中,∠A,∠B都是锐角,若sinA=,cosB=,则∠C= .
16、如果3sinα=+1,则∠α= ?? .(精确到0.1度)
17、已知在Rt△ABC中,∠C=90°,sin A=,则tan B的值为 .
18、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tanA+tanB的值为 ??? .
三、简答题
19、在Rt△ABC中,∠C=90°,BC∶AC=3∶4,求∠A的三个三角函数值.
20、设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件求∠B的三个三角函数值:(自己画图)
(1)a=1,b=2;??????? (2)a=5,c=13.
21、先化简,再求代数式(+)÷的值,其中x=sin60°﹣cos45°
22、先化简,再求值:(﹣)÷,其中x=2sin30°+2cos45°.
23、如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠ADE的正弦值.
24、小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(1)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
参考答案
一、选择题
1、A;2、C.;3、A;4、C;5、A;6、C;7、C;8、D.;9、D;10、B;11、D.;12、A;
二、填空题
13、
14、 直角
15、60°? ? ???
16、65.5°
17、.
18、3
三、简答题
19、
20、
21、解:原式=(﹣)?
=?
=
=,
当x=sin60°﹣cos45°=×﹣×=时,
原式==﹣17.
22、:原式=÷
=×
=
∵x=2sin30°+2cos45°
=2×+2×=3,
∴原式=.
23、解:(1)CD与⊙O相切.
理由是:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切.
(2)连接BE,由圆周角定理,得∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×3=6(cm).
在Rt△ABE中,
sin∠ABE==,
∴sin∠ADE=sin∠ABE=.
24、解1:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
