人教版九年级数学下册 28.2 :解直角三角形及其应用 同步练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册 28.2 :解直角三角形及其应用 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 219.5KB | ||
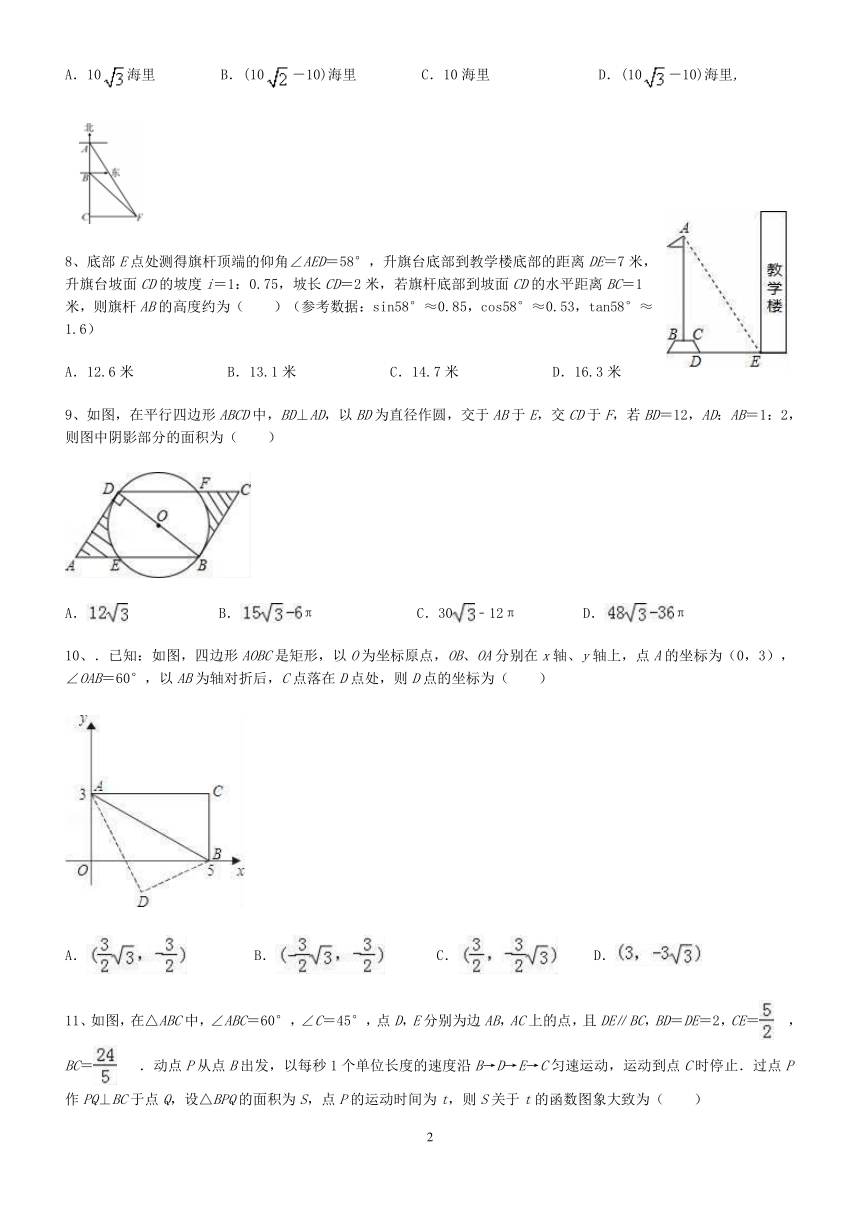
| 资源类型 | 教案 | ||
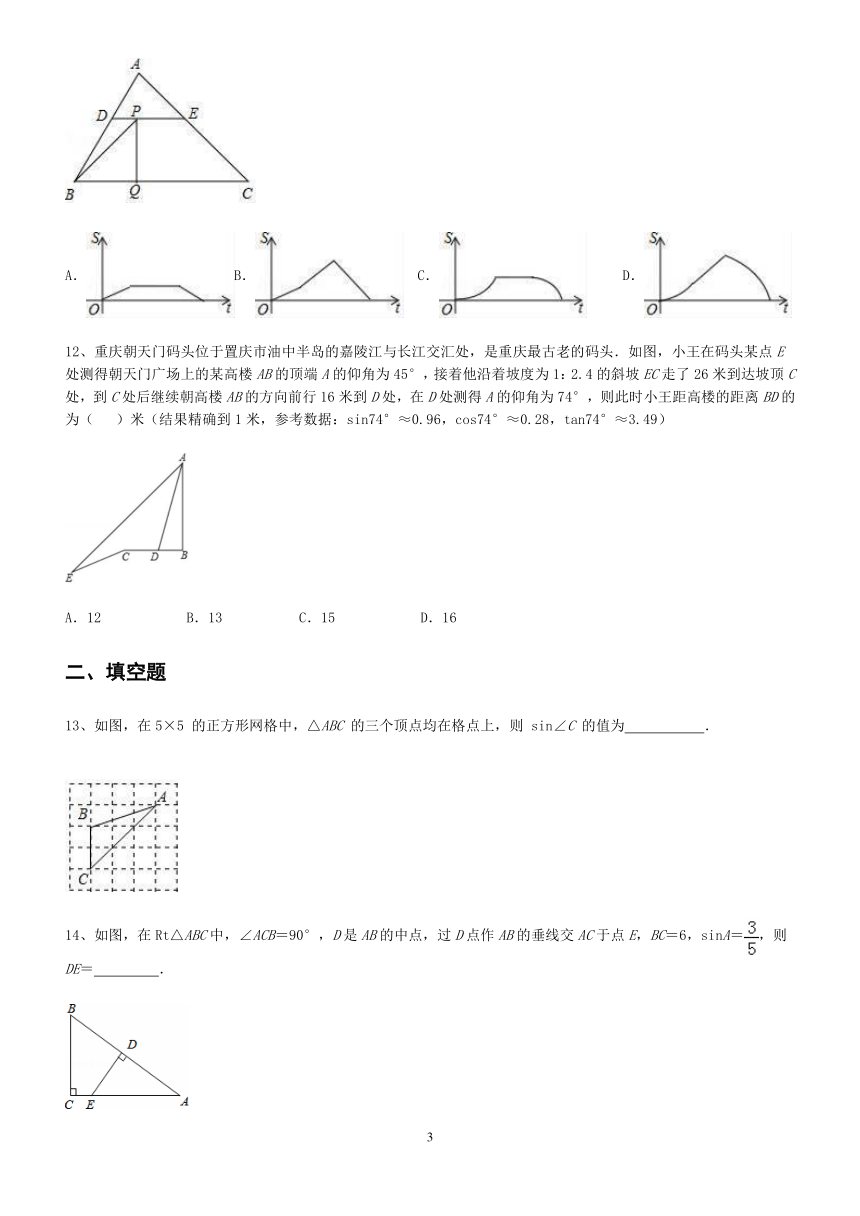
| 版本资源 | 人教版 | ||
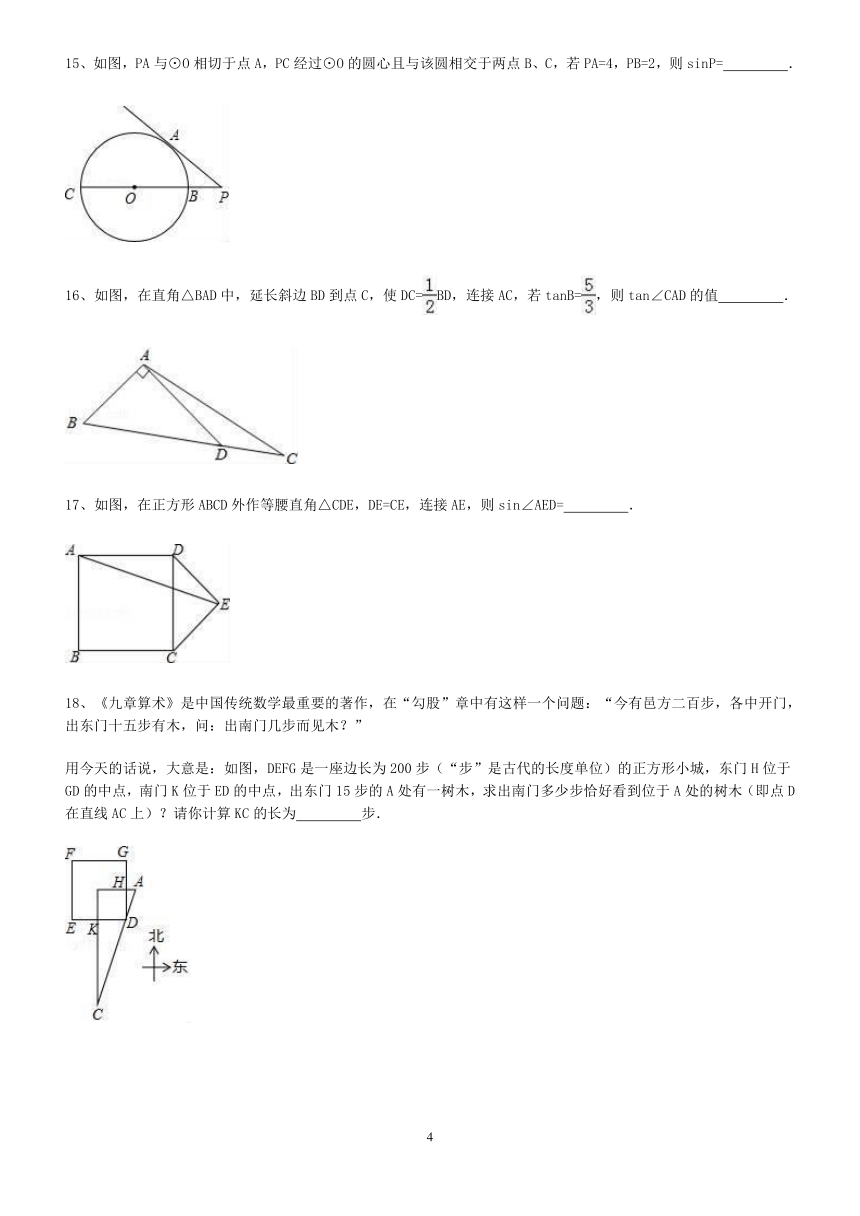
| 科目 | 数学 | ||
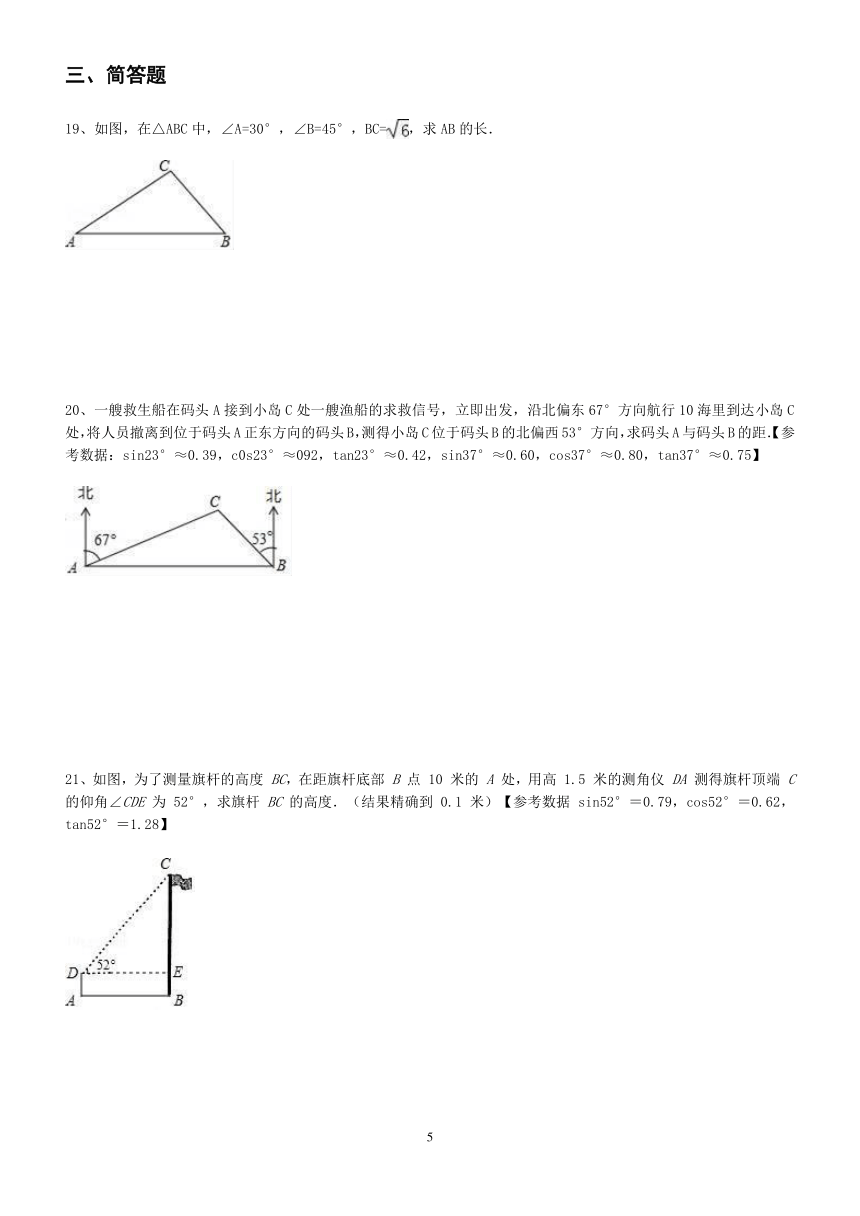
| 更新时间 | 2020-03-05 23:10:46 | ||
图片预览

文档简介
解直角三角形及其应用 同步练习
1、选择题
1、如果△ABC中,∠C=90°,sinA=,那么下列等式不正确的是(?? )
A.cosA= ?? B.cotA=? ?C. sinB=?? D. tanB=.
2、在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(???? )
A.?? ? B.?? ???? C.? ? ??? D..
3、在中,,如果,,那么的长是(? )
A. ? B. C. D..
4、已知在Rt△ABC中,∠C=90°,BC=5,那么AB的长为(??? )
A.5sinA B.5cosA C. D..
5、为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
A. km2????? B. km2?????? C. km2????? D. km2?
6、如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为(??? )
A.千米;??? B.千米;
C.千米;??? D.千米.
7、如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里???? B.(10-10)海里???? C.10海里??????? D.(10-10)海里,
????
8、底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为( )(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)
A.12.6米?????? B.13.1米?????? C.14.7米?????? D.16.3米
9、如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
A.??? B.π??? ??? C.30﹣12π???? D.π
10、.已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )
A. B.? C.?? D.
11、如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=,BC=.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A.B.?C.?? D.
12、重庆朝天门码头位于置庆市油中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如图,小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°,接着他沿着坡度为1:2.4的斜坡EC走了26米到达坡顶C处,到C处后继续朝高楼AB的方向前行16米到D处,在D处测得A的仰角为74°,则此时小王距高楼的距离BD的为(? )米(结果精确到1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
?
A.12 B.13? ? C.15? ? D.16
二、填空题
13、如图,在5×5 的正方形网格中,△ABC 的三个顶点均在格点上,则 sin∠C 的值为 ?????.
14、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= ?? .
15、如图,PA与⊙O相切于点A,PC经过⊙O的圆心且与该圆相交于两点B、C,若PA=4,PB=2,则sinP= ?? .
16、如图,在直角△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值 ?? .
17、如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED= ?? .
18、《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 ?? 步.
三、简答题
19、如图,在△ABC中,∠A=30°,∠B=45°,BC=,求AB的长.
20、一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距.【参考数据:sin23°≈0.39,c0s23°≈092,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】
21、如图,为了测量旗杆的高度 BC,在距旗杆底部 B 点 10 米的 A 处,用高 1.5 米的测角仪 DA 测得旗杆顶端 C 的仰角∠CDE 为 52°,求旗杆 BC 的高度.(结果精确到 0.1 米)【参考数据 sin52°=0.79,cos52°=0.62,tan52°=1.28】
22、小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75m,请求出热气球离地面的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈).
23、如图,在 Rt△ABC 中,∠C=90°,点 D 在 BC 边上,∠ADC=45°,BD=2,tanB=
(1)求AC和AB的长;
(2)求sin∠BAD的值.
24、如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
参考答案
一、选择题
1、A;2、A;;3、A;;4、C;;5、D.;6、A;7、D;8、B;9、C;10、A;11、D;12、A;
二、填空题
13、
14、
15、
16、.
17、
18、
三、简答题
19、解;过点C作CD⊥AB,交AB于D.
∵∠B=45°,
∴CD=BD,
∵BC=,
∴BD=,
∵∠A=30°,
∴tan30°=,
∴AD===3,
∴AB=AD+BD=3+.
20、解:过点C作CD⊥AB于点D,
由题意,得:∠BAC=23°,∠ABC=37°,AC=10,
在Rt△ADC中,AD=ACcos23°=10×0.92=9.2,
∴CD=ACsin23°=10×0.39=3.9,
在Rt△BCD中,BD===5.2,
则AB=AD+BD=9.2+5.2=14.4,
答:码头A与码头B的距离14.4海里.
21、解:过点 D 作 DE⊥BC 交 BC 于 E,
在△CDE 中,有 CE=tan52°×DE=1.28×10≈12.8, 故 BC=BE+CE=1.5+12.8≈14.3,
答:旗杆的高度为 14.3 米.
22、?解:过A作AD⊥BC,
在Rt△ACD中,tan∠ACD=,即CD==AD,
在Rt△ABD中,tan∠ABD=,即BD==AD,
由题意得:AD﹣AD=75,
解得:AD=300m,
则热气球离底面的高度是300m.
23、解:(1)如图,在 Rt△ABC 中,
∵tanB= = ,
∴设 AC=3x、BC=4x,
∵BD=2,
∴DC=BC﹣BD=4x﹣2,
∵∠ADC=45°,
∴AC=DC,即 4x﹣2=3x, 解得:x=2,
则 AC=6、BC=8,
∴AB==10;
(2)作 DE⊥AB 于点 E,
由 tanB== 可设 DE=3a,则 BE=4a,
∵DE2+BE2=BD2,且 BD=2,
∴(3a)2+(4a)2=22,解得:a=(负值舍去),
∴DE=3a= ,
∵AD= =6 ,
∴sin∠BAD= = .
24、解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD?sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米).
1、选择题
1、如果△ABC中,∠C=90°,sinA=,那么下列等式不正确的是(?? )
A.cosA= ?? B.cotA=? ?C. sinB=?? D. tanB=.
2、在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(???? )
A.?? ? B.?? ???? C.? ? ??? D..
3、在中,,如果,,那么的长是(? )
A. ? B. C. D..
4、已知在Rt△ABC中,∠C=90°,BC=5,那么AB的长为(??? )
A.5sinA B.5cosA C. D..
5、为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
A. km2????? B. km2?????? C. km2????? D. km2?
6、如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为(??? )
A.千米;??? B.千米;
C.千米;??? D.千米.
7、如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里???? B.(10-10)海里???? C.10海里??????? D.(10-10)海里,
????
8、底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为( )(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)
A.12.6米?????? B.13.1米?????? C.14.7米?????? D.16.3米
9、如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
A.??? B.π??? ??? C.30﹣12π???? D.π
10、.已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )
A. B.? C.?? D.
11、如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=,BC=.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A.B.?C.?? D.
12、重庆朝天门码头位于置庆市油中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如图,小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°,接着他沿着坡度为1:2.4的斜坡EC走了26米到达坡顶C处,到C处后继续朝高楼AB的方向前行16米到D处,在D处测得A的仰角为74°,则此时小王距高楼的距离BD的为(? )米(结果精确到1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
?
A.12 B.13? ? C.15? ? D.16
二、填空题
13、如图,在5×5 的正方形网格中,△ABC 的三个顶点均在格点上,则 sin∠C 的值为 ?????.
14、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= ?? .
15、如图,PA与⊙O相切于点A,PC经过⊙O的圆心且与该圆相交于两点B、C,若PA=4,PB=2,则sinP= ?? .
16、如图,在直角△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值 ?? .
17、如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED= ?? .
18、《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 ?? 步.
三、简答题
19、如图,在△ABC中,∠A=30°,∠B=45°,BC=,求AB的长.
20、一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距.【参考数据:sin23°≈0.39,c0s23°≈092,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】
21、如图,为了测量旗杆的高度 BC,在距旗杆底部 B 点 10 米的 A 处,用高 1.5 米的测角仪 DA 测得旗杆顶端 C 的仰角∠CDE 为 52°,求旗杆 BC 的高度.(结果精确到 0.1 米)【参考数据 sin52°=0.79,cos52°=0.62,tan52°=1.28】
22、小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75m,请求出热气球离地面的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈).
23、如图,在 Rt△ABC 中,∠C=90°,点 D 在 BC 边上,∠ADC=45°,BD=2,tanB=
(1)求AC和AB的长;
(2)求sin∠BAD的值.
24、如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
参考答案
一、选择题
1、A;2、A;;3、A;;4、C;;5、D.;6、A;7、D;8、B;9、C;10、A;11、D;12、A;
二、填空题
13、
14、
15、
16、.
17、
18、
三、简答题
19、解;过点C作CD⊥AB,交AB于D.
∵∠B=45°,
∴CD=BD,
∵BC=,
∴BD=,
∵∠A=30°,
∴tan30°=,
∴AD===3,
∴AB=AD+BD=3+.
20、解:过点C作CD⊥AB于点D,
由题意,得:∠BAC=23°,∠ABC=37°,AC=10,
在Rt△ADC中,AD=ACcos23°=10×0.92=9.2,
∴CD=ACsin23°=10×0.39=3.9,
在Rt△BCD中,BD===5.2,
则AB=AD+BD=9.2+5.2=14.4,
答:码头A与码头B的距离14.4海里.
21、解:过点 D 作 DE⊥BC 交 BC 于 E,
在△CDE 中,有 CE=tan52°×DE=1.28×10≈12.8, 故 BC=BE+CE=1.5+12.8≈14.3,
答:旗杆的高度为 14.3 米.
22、?解:过A作AD⊥BC,
在Rt△ACD中,tan∠ACD=,即CD==AD,
在Rt△ABD中,tan∠ABD=,即BD==AD,
由题意得:AD﹣AD=75,
解得:AD=300m,
则热气球离底面的高度是300m.
23、解:(1)如图,在 Rt△ABC 中,
∵tanB= = ,
∴设 AC=3x、BC=4x,
∵BD=2,
∴DC=BC﹣BD=4x﹣2,
∵∠ADC=45°,
∴AC=DC,即 4x﹣2=3x, 解得:x=2,
则 AC=6、BC=8,
∴AB==10;
(2)作 DE⊥AB 于点 E,
由 tanB== 可设 DE=3a,则 BE=4a,
∵DE2+BE2=BD2,且 BD=2,
∴(3a)2+(4a)2=22,解得:a=(负值舍去),
∴DE=3a= ,
∵AD= =6 ,
∴sin∠BAD= = .
24、解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD?sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米).
