2019-2020学年河北省张家口市桥西区八年级(上)期末数学试卷 解析版
文档属性
| 名称 | 2019-2020学年河北省张家口市桥西区八年级(上)期末数学试卷 解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 06:45:31 | ||
图片预览



文档简介
2019-2020学年河北省张家口市桥西区八年级(上)期末数学试卷
一、精心选择(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂在答题卡上,填在试卷上无效.)
1.(2分)要使分式有意义,则x应满足的条件是( )
A.x>5 B.x≠5 C.x≥5 D.x=5
2.(2分)下列图形中,中心对称图形是( )
A. B.
C. D.
3.(2分)把319000写成a×10n(1≤a≤10,n为整数)的形式,则a为( )
A.5 B.4 C.3.2 D.3.19
4.(2分)下列实数中,无理数是( )
A. B.﹣0.3 C. D.
5.(2分)a,b是两个连续整数,若a<<b,则a+b的值是( )
A.7 B.9 C.21 D.25
6.(2分)下列各式运算正确的是( )
A.=±2 B.3﹣=3 C.=3 D.×=
7.(2分)如图所示的两个三角形全等,则∠1的度数是( )
A.50° B.72° C.58° D.82°
8.(2分)下列运算结果为x﹣1的是( )
A.1﹣ B.?
C.÷ D.
9.(2分)如图,在长方形ABCD中,点E,点F分别为BC和AB上任意一点,点B和点M关于EF对称,EN是∠MEC的平分线,若∠BFE=60°,则∠MEN的度数是( )
A.30° B.60° C.45° D.50°
10.(2分)下列说法正确的是( )
A.等腰直角三角形的高线、中线、角平分线互相重合
B.有两条边相等的两个直角三角形全等
C.四边形具有稳定性
D.角平分线上的点到角两边的距离相等
11.(2分)若关于x的分式方程=有增根,则m的值是( )
A.m=﹣1 B.m=1 C.m=﹣2 D.m=2
12.(2分)如图,在△OAB中,∠AOB=90°,OD⊥AB,∠A=30°,AB=20,则OD是( )
A.5 B.5 C.10 D.10
13.(2分)如图,已知直线l1∥l2,点A,D和点B,C,E,F分别在直线l1,l2上,△ABC和△DEF的面积之比为1:4,边EF比边BC长27cm,则BC=( )cm.
A.3 B.12 C.9 D.18
14.(2分)中国首列商用磁浮列车平均速度为akm/h,计划提速20km/h,已知从A地到B地路程为360km,那么提速后从甲地到乙地节约的时间表示为( )
A. B.
C. D.
15.(2分)已知为n正整数,也是正整数,那么满足条件的n的最小值是( )
A.3 B.12 C.2 D.192
16.(2分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A2019B2019A2020的边长是( )
A.4038 B.4036 C.22018 D.22019
二、准确填空(本大题共3个小题,17、18题每小题3分,19题每空2分,共10分.)
17.(3分)计算:= .
18.(3分)一把工艺剪刀可以抽象为下图,其中AC=AB,若剪刀张开的角为40°,则∠B= °.
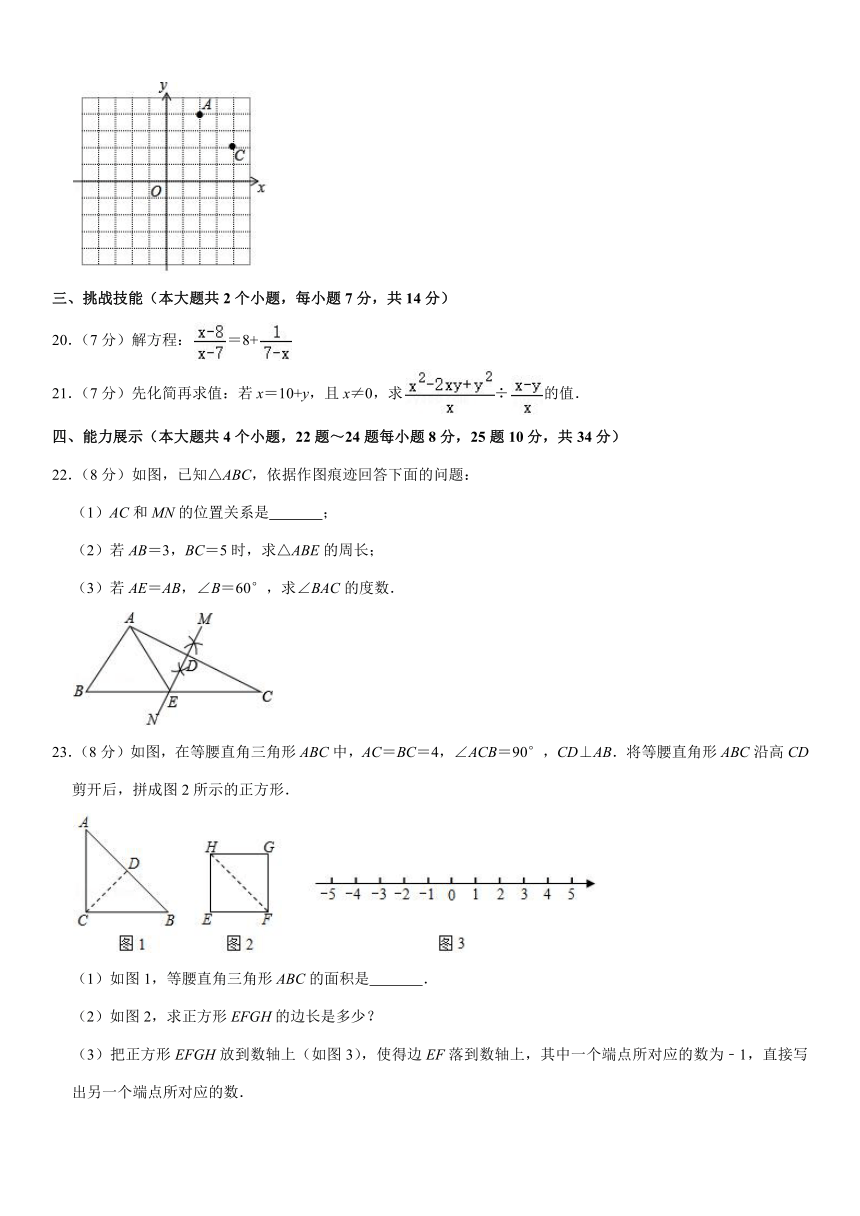
19.(4分)如图,网格纸上每个小正方形的边长为1,点A,点C均在格点上,点P为x轴上任意一点,则AC= ;△PAC周长的最小值为 .
三、挑战技能(本大题共2个小题,每小题7分,共14分)
20.(7分)解方程:=8+
21.(7分)先化简再求值:若x=10+y,且x≠0,求÷的值.
四、能力展示(本大题共4个小题,22题~24题每小题8分,25题10分,共34分)
22.(8分)如图,已知△ABC,依据作图痕迹回答下面的问题:
(1)AC和MN的位置关系是 ;
(2)若AB=3,BC=5时,求△ABE的周长;
(3)若AE=AB,∠B=60°,求∠BAC的度数.
23.(8分)如图,在等腰直角三角形ABC中,AC=BC=4,∠ACB=90°,CD⊥AB.将等腰直角形ABC沿高CD剪开后,拼成图2所示的正方形.
(1)如图1,等腰直角三角形ABC的面积是 .
(2)如图2,求正方形EFGH的边长是多少?
(3)把正方形EFGH放到数轴上(如图3),使得边EF落到数轴上,其中一个端点所对应的数为﹣1,直接写出另一个端点所对应的数.
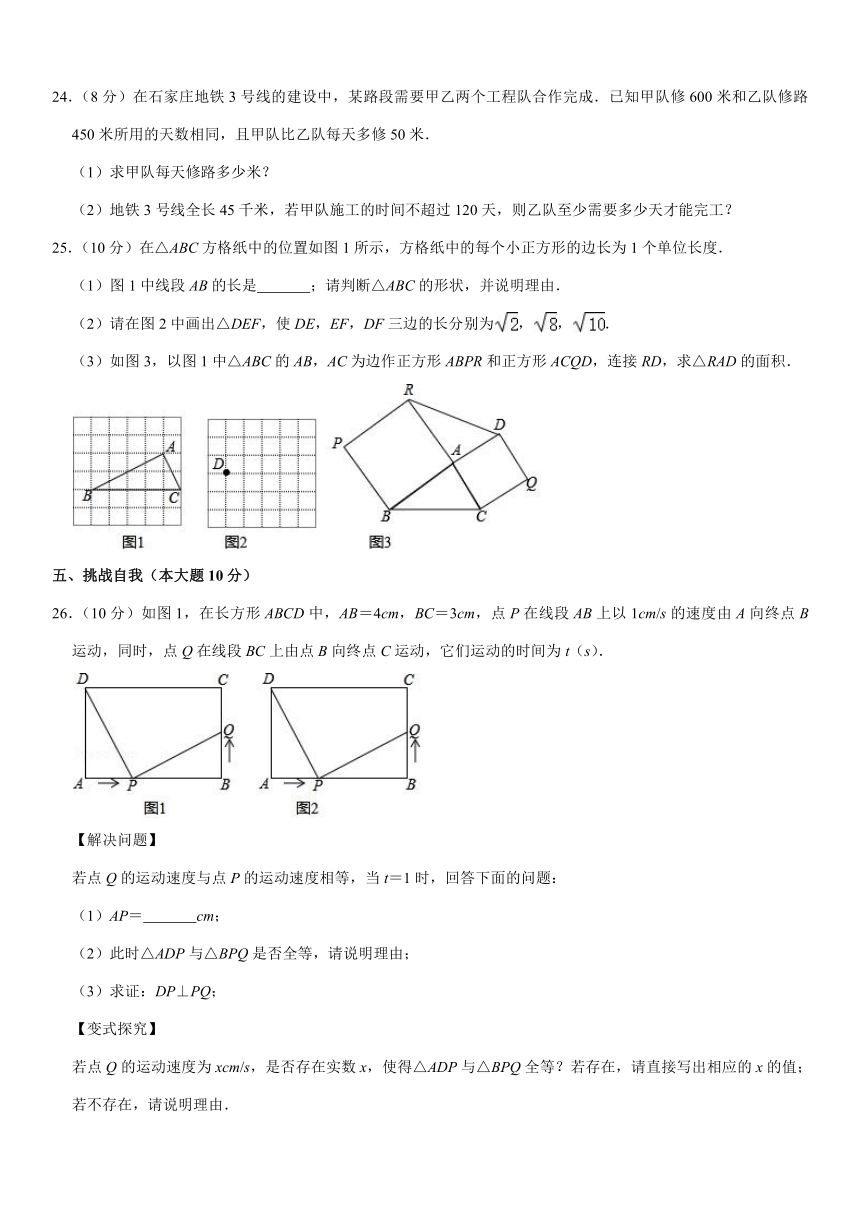
24.(8分)在石家庄地铁3号线的建设中,某路段需要甲乙两个工程队合作完成.已知甲队修600米和乙队修路450米所用的天数相同,且甲队比乙队每天多修50米.
(1)求甲队每天修路多少米?
(2)地铁3号线全长45千米,若甲队施工的时间不超过120天,则乙队至少需要多少天才能完工?
25.(10分)在△ABC方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
(1)图1中线段AB的长是 ;请判断△ABC的形状,并说明理由.
(2)请在图2中画出△DEF,使DE,EF,DF三边的长分别为,,.
(3)如图3,以图1中△ABC的AB,AC为边作正方形ABPR和正方形ACQD,连接RD,求△RAD的面积.
五、挑战自我(本大题10分)
26.(10分)如图1,在长方形ABCD中,AB=4cm,BC=3cm,点P在线段AB上以1cm/s的速度由A向终点B运动,同时,点Q在线段BC上由点B向终点C运动,它们运动的时间为t(s).
【解决问题】
若点Q的运动速度与点P的运动速度相等,当t=1时,回答下面的问题:
(1)AP= cm;
(2)此时△ADP与△BPQ是否全等,请说明理由;
(3)求证:DP⊥PQ;
【变式探究】
若点Q的运动速度为xcm/s,是否存在实数x,使得△ADP与△BPQ全等?若存在,请直接写出相应的x的值;若不存在,请说明理由.
2019-2020学年河北省张家口市桥西区八年级(上)期末数学试卷
参考答案与试题解析
一、精心选择(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂在答题卡上,填在试卷上无效.)
1.【解答】解:依题意得:x﹣5≠0,
解得x≠5.
故选:B.
2.【解答】解:A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、是中心对称图形,故此选项正确;
D、不是中心对称图形,故此选项错误;
故选:C.
3.【解答】解:319000=3.19×105,
故a=3.19.
故选:D.
4.【解答】解:A、是分数,分数是有理数,故本选项错误;
B、﹣0.3是有理数,故本选项错误;
C、是无理数,故本选项正确;
D、=3是有理数,故本选项错误.
故选:C.
5.【解答】解:∵3<<4,
∴a=3,b=4,
∴a+b=7,
故选:A.
6.【解答】解:A、原式=2,所以A选项的计算错误;
B、原式=2,所以B选项的计算错误;
C、原式=2,所以C选项的计算错误;
D、原式==,所以D选项的计算正确.
故选:D.
7.【解答】解:∠A=180°﹣∠B﹣∠C=50°,
∵两个三角形全等,
∴∠1=∠A=50°,
故选:A.
8.【解答】解:A、1﹣=,故此选项错误;
B、原式=?=x﹣1,故此选项正确;
C、原式=?(x﹣1)=,故此选项错误;
D、原式==x+1,故此选项错误;
故选:B.
9.【解答】解:∵∠BFE=60°,∠B=90°,
∴∠BEF=30°,
∵点B和点M关于EF对称,
∴∠BEF=∠MEF=30°,
∴∠MEC=180°﹣30°﹣30°=120°,
∵EN是∠MEC的平分线,
∴∠MEN=60°,
故选:B.
10.【解答】解:A、错误.应该是等腰直角三角形的底边上的高线、中线、角平分线互相重合.
B、错误.应该是对应相等.
C、错误.四边形没有稳定性.
D、正确.
故选:D.
11.【解答】解:方程两边同时乘以x﹣1,得
m+1=﹣x,
解得:x=﹣m﹣1,
∵方程有增根,
∴x=1,
∴﹣m﹣1=1,
∴m=﹣2,
故选:C.
12.【解答】解:∵△OAB中,∠AOB=90°,∠A=30°,
∴∠B=60°,
又OD⊥AB,
∴∠BOD=30°,
在Rt△ABC中,∠A=30°,AB=20,
∴OB=AB=10,
在Rt△BOD中,∠BOD=30°,
∴BD=OB=5,
∴OD===5,
故选:A.
13.【解答】解:∵直线l1∥l2,
∴△ABC和△DEF是不等底、等高的三角形,
∵△ABC和△DEF的面积之比为1:4,
∴BC:EF=1:4,
设BC=x,则EF=4x,
∵边EF比边BC长27cm,
∴4x﹣x=27,解得x=9,
∴BC=9cm,
故选:C.
14.【解答】解:由题意可得:
﹣=.
故选:A.
15.【解答】解:=8,
∵也是正整数,
∴3n为完全平方数,
∴n的最小值是3.
故选:A.
16.【解答】解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∵∠MON=30°,
∴∠A1B1O=30°,
∴A1B1=OA1,
∴A1B1=A1A2=OA1,
同理可得A2B2=A2A3=OA2=2OA1,
∴A3B3=A3A4=OA3=2OA2=22?OA1,
A4B4=A4A5=OA4=2OA3=23?OA1,
…
∴A2019B2019=A2019A2020=OA2019=22018?OA1=22019.
故选:D.
二、准确填空(本大题共3个小题,17、18题每小题3分,19题每空2分,共10分.)
17.【解答】解:∵23=8
∴=2
故答案为:2.
18.【解答】解:∵CA=BA,∠CAB=40°,
∴∠B=(180°﹣40°)=70°,
故答案为:70.
19.【解答】解:AC==2,
如图,作点C关于x轴的对称点C′,连接AC′,与x轴交于点P,
则AP+PC=AP+PC′=AC′,
此时AP+PC取得最小值,最小值为=2,
所以△PAC周长的最小值为2+2,
故答案为:2,2+2.
三、挑战技能(本大题共2个小题,每小题7分,共14分)
20.【解答】解:去分母得:x﹣8=8x﹣56﹣1,
移项合并得:﹣7x=﹣49,
解得:x=7,
经检验x=7是增根,分式方程无解.
21.【解答】解:原式=?=x﹣y,
∵x=10+y,
∴x﹣y=10,
∴原式=x﹣y=10.
四、能力展示(本大题共4个小题,22题~24题每小题8分,25题10分,共34分)
22.【解答】解:(1)根据作图痕迹可知:
MN是AD的垂直平分线,
所以AC和MN的位置关系是垂直,
故答案为垂直;
(2)AB=3,BC=5,
∵MN是AC的垂直平分线,
∴EA=EC
∴△ABE的周长
=AB+AE+BE
=AB+EC+BE
=AB+BC
=3+5
=8;
答:△ABE的周长为8.
(3)∵AE=AB,∠B=60°,
∴△ABE是等边三角形,
∴∠AEB=60°
∵AE=CE
∴∠C=∠CAE=30°,
∴∠BAC=90°.
答:∠BAC的度数为90°.
23.【解答】解:(1)S△ABC=?AC?BC=×4×4=8,
故答案为8.
(2)由题意EF2=8,
∴EF=2,
∴正方形EFGH的边长为2.
(3)另一端点对应的数是﹣1+2或﹣1﹣2.
24.【解答】解:(1)设甲队每天修路x米,则乙队每天修路(x﹣50)米,
依题意,得:=,
解得:x=200,
经检验,x=200是原方程的解,且符合题意.
答:甲队每天修路200米.
(2)设乙队需要y天才能完工,
依题意,得:45000﹣(200﹣50)y≥200×120,
解得:y≤140.
答:乙队至少需要140天才能完工.
25.【解答】解:(1)AB==2,
故答案为2.
△ABC是直角三角形.
理由:∵AB=2,AC==,BC=5,
∴AB2+AC2=20+5=25=BC2,
∴∠BAC=90°,
∴△ABC是直角三角形.
(2)如图2中,△DEF即为所求.
(3)如图3中,由题意AB=AR=2,AC=AD=,∠BAC=∠BAR=∠CAD=90°,
∴∠RAD=360°﹣3×90°=90°,
∴S△ADR=?AR?AD=×2×=5.
五、挑战自我(本大题10分)
26.【解答】解:【解决问题】(1)由题意AP=1×1=1(cm),BQ=1×1=1cm,
故答案为1.
(2)∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵AD=PB=3,PA=BQ=1,
∴△ADP≌△BPQ(SAS).
(3)∵△ADP≌△BPQ,
∴∠APD=∠PQB,
∵∠BPQ+∠PQB=90°,
∴∠APD+∠BPQ=90°,
∴∠DPQ=90°,
∴DP⊥PQ.
【变式探究】①当x=1cm/s时,t=1时,两个三角形全等.
②当AP=PB,BQ=AD时,两个三角形全等,
此时t==2,VQ=cm/s,
∴x=cm/s.
综上所述,满足条件的x的值为1或.
一、精心选择(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂在答题卡上,填在试卷上无效.)
1.(2分)要使分式有意义,则x应满足的条件是( )
A.x>5 B.x≠5 C.x≥5 D.x=5
2.(2分)下列图形中,中心对称图形是( )
A. B.
C. D.
3.(2分)把319000写成a×10n(1≤a≤10,n为整数)的形式,则a为( )
A.5 B.4 C.3.2 D.3.19
4.(2分)下列实数中,无理数是( )
A. B.﹣0.3 C. D.
5.(2分)a,b是两个连续整数,若a<<b,则a+b的值是( )
A.7 B.9 C.21 D.25
6.(2分)下列各式运算正确的是( )
A.=±2 B.3﹣=3 C.=3 D.×=
7.(2分)如图所示的两个三角形全等,则∠1的度数是( )
A.50° B.72° C.58° D.82°
8.(2分)下列运算结果为x﹣1的是( )
A.1﹣ B.?
C.÷ D.
9.(2分)如图,在长方形ABCD中,点E,点F分别为BC和AB上任意一点,点B和点M关于EF对称,EN是∠MEC的平分线,若∠BFE=60°,则∠MEN的度数是( )
A.30° B.60° C.45° D.50°
10.(2分)下列说法正确的是( )
A.等腰直角三角形的高线、中线、角平分线互相重合
B.有两条边相等的两个直角三角形全等
C.四边形具有稳定性
D.角平分线上的点到角两边的距离相等
11.(2分)若关于x的分式方程=有增根,则m的值是( )
A.m=﹣1 B.m=1 C.m=﹣2 D.m=2
12.(2分)如图,在△OAB中,∠AOB=90°,OD⊥AB,∠A=30°,AB=20,则OD是( )
A.5 B.5 C.10 D.10
13.(2分)如图,已知直线l1∥l2,点A,D和点B,C,E,F分别在直线l1,l2上,△ABC和△DEF的面积之比为1:4,边EF比边BC长27cm,则BC=( )cm.
A.3 B.12 C.9 D.18
14.(2分)中国首列商用磁浮列车平均速度为akm/h,计划提速20km/h,已知从A地到B地路程为360km,那么提速后从甲地到乙地节约的时间表示为( )
A. B.
C. D.
15.(2分)已知为n正整数,也是正整数,那么满足条件的n的最小值是( )
A.3 B.12 C.2 D.192
16.(2分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A2019B2019A2020的边长是( )
A.4038 B.4036 C.22018 D.22019
二、准确填空(本大题共3个小题,17、18题每小题3分,19题每空2分,共10分.)
17.(3分)计算:= .
18.(3分)一把工艺剪刀可以抽象为下图,其中AC=AB,若剪刀张开的角为40°,则∠B= °.
19.(4分)如图,网格纸上每个小正方形的边长为1,点A,点C均在格点上,点P为x轴上任意一点,则AC= ;△PAC周长的最小值为 .
三、挑战技能(本大题共2个小题,每小题7分,共14分)
20.(7分)解方程:=8+
21.(7分)先化简再求值:若x=10+y,且x≠0,求÷的值.
四、能力展示(本大题共4个小题,22题~24题每小题8分,25题10分,共34分)
22.(8分)如图,已知△ABC,依据作图痕迹回答下面的问题:
(1)AC和MN的位置关系是 ;
(2)若AB=3,BC=5时,求△ABE的周长;
(3)若AE=AB,∠B=60°,求∠BAC的度数.
23.(8分)如图,在等腰直角三角形ABC中,AC=BC=4,∠ACB=90°,CD⊥AB.将等腰直角形ABC沿高CD剪开后,拼成图2所示的正方形.
(1)如图1,等腰直角三角形ABC的面积是 .
(2)如图2,求正方形EFGH的边长是多少?
(3)把正方形EFGH放到数轴上(如图3),使得边EF落到数轴上,其中一个端点所对应的数为﹣1,直接写出另一个端点所对应的数.
24.(8分)在石家庄地铁3号线的建设中,某路段需要甲乙两个工程队合作完成.已知甲队修600米和乙队修路450米所用的天数相同,且甲队比乙队每天多修50米.
(1)求甲队每天修路多少米?
(2)地铁3号线全长45千米,若甲队施工的时间不超过120天,则乙队至少需要多少天才能完工?
25.(10分)在△ABC方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
(1)图1中线段AB的长是 ;请判断△ABC的形状,并说明理由.
(2)请在图2中画出△DEF,使DE,EF,DF三边的长分别为,,.
(3)如图3,以图1中△ABC的AB,AC为边作正方形ABPR和正方形ACQD,连接RD,求△RAD的面积.
五、挑战自我(本大题10分)
26.(10分)如图1,在长方形ABCD中,AB=4cm,BC=3cm,点P在线段AB上以1cm/s的速度由A向终点B运动,同时,点Q在线段BC上由点B向终点C运动,它们运动的时间为t(s).
【解决问题】
若点Q的运动速度与点P的运动速度相等,当t=1时,回答下面的问题:
(1)AP= cm;
(2)此时△ADP与△BPQ是否全等,请说明理由;
(3)求证:DP⊥PQ;
【变式探究】
若点Q的运动速度为xcm/s,是否存在实数x,使得△ADP与△BPQ全等?若存在,请直接写出相应的x的值;若不存在,请说明理由.
2019-2020学年河北省张家口市桥西区八年级(上)期末数学试卷
参考答案与试题解析
一、精心选择(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂在答题卡上,填在试卷上无效.)
1.【解答】解:依题意得:x﹣5≠0,
解得x≠5.
故选:B.
2.【解答】解:A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、是中心对称图形,故此选项正确;
D、不是中心对称图形,故此选项错误;
故选:C.
3.【解答】解:319000=3.19×105,
故a=3.19.
故选:D.
4.【解答】解:A、是分数,分数是有理数,故本选项错误;
B、﹣0.3是有理数,故本选项错误;
C、是无理数,故本选项正确;
D、=3是有理数,故本选项错误.
故选:C.
5.【解答】解:∵3<<4,
∴a=3,b=4,
∴a+b=7,
故选:A.
6.【解答】解:A、原式=2,所以A选项的计算错误;
B、原式=2,所以B选项的计算错误;
C、原式=2,所以C选项的计算错误;
D、原式==,所以D选项的计算正确.
故选:D.
7.【解答】解:∠A=180°﹣∠B﹣∠C=50°,
∵两个三角形全等,
∴∠1=∠A=50°,
故选:A.
8.【解答】解:A、1﹣=,故此选项错误;
B、原式=?=x﹣1,故此选项正确;
C、原式=?(x﹣1)=,故此选项错误;
D、原式==x+1,故此选项错误;
故选:B.
9.【解答】解:∵∠BFE=60°,∠B=90°,
∴∠BEF=30°,
∵点B和点M关于EF对称,
∴∠BEF=∠MEF=30°,
∴∠MEC=180°﹣30°﹣30°=120°,
∵EN是∠MEC的平分线,
∴∠MEN=60°,
故选:B.
10.【解答】解:A、错误.应该是等腰直角三角形的底边上的高线、中线、角平分线互相重合.
B、错误.应该是对应相等.
C、错误.四边形没有稳定性.
D、正确.
故选:D.
11.【解答】解:方程两边同时乘以x﹣1,得
m+1=﹣x,
解得:x=﹣m﹣1,
∵方程有增根,
∴x=1,
∴﹣m﹣1=1,
∴m=﹣2,
故选:C.
12.【解答】解:∵△OAB中,∠AOB=90°,∠A=30°,
∴∠B=60°,
又OD⊥AB,
∴∠BOD=30°,
在Rt△ABC中,∠A=30°,AB=20,
∴OB=AB=10,
在Rt△BOD中,∠BOD=30°,
∴BD=OB=5,
∴OD===5,
故选:A.
13.【解答】解:∵直线l1∥l2,
∴△ABC和△DEF是不等底、等高的三角形,
∵△ABC和△DEF的面积之比为1:4,
∴BC:EF=1:4,
设BC=x,则EF=4x,
∵边EF比边BC长27cm,
∴4x﹣x=27,解得x=9,
∴BC=9cm,
故选:C.
14.【解答】解:由题意可得:
﹣=.
故选:A.
15.【解答】解:=8,
∵也是正整数,
∴3n为完全平方数,
∴n的最小值是3.
故选:A.
16.【解答】解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∵∠MON=30°,
∴∠A1B1O=30°,
∴A1B1=OA1,
∴A1B1=A1A2=OA1,
同理可得A2B2=A2A3=OA2=2OA1,
∴A3B3=A3A4=OA3=2OA2=22?OA1,
A4B4=A4A5=OA4=2OA3=23?OA1,
…
∴A2019B2019=A2019A2020=OA2019=22018?OA1=22019.
故选:D.
二、准确填空(本大题共3个小题,17、18题每小题3分,19题每空2分,共10分.)
17.【解答】解:∵23=8
∴=2
故答案为:2.
18.【解答】解:∵CA=BA,∠CAB=40°,
∴∠B=(180°﹣40°)=70°,
故答案为:70.
19.【解答】解:AC==2,
如图,作点C关于x轴的对称点C′,连接AC′,与x轴交于点P,
则AP+PC=AP+PC′=AC′,
此时AP+PC取得最小值,最小值为=2,
所以△PAC周长的最小值为2+2,
故答案为:2,2+2.
三、挑战技能(本大题共2个小题,每小题7分,共14分)
20.【解答】解:去分母得:x﹣8=8x﹣56﹣1,
移项合并得:﹣7x=﹣49,
解得:x=7,
经检验x=7是增根,分式方程无解.
21.【解答】解:原式=?=x﹣y,
∵x=10+y,
∴x﹣y=10,
∴原式=x﹣y=10.
四、能力展示(本大题共4个小题,22题~24题每小题8分,25题10分,共34分)
22.【解答】解:(1)根据作图痕迹可知:
MN是AD的垂直平分线,
所以AC和MN的位置关系是垂直,
故答案为垂直;
(2)AB=3,BC=5,
∵MN是AC的垂直平分线,
∴EA=EC
∴△ABE的周长
=AB+AE+BE
=AB+EC+BE
=AB+BC
=3+5
=8;
答:△ABE的周长为8.
(3)∵AE=AB,∠B=60°,
∴△ABE是等边三角形,
∴∠AEB=60°
∵AE=CE
∴∠C=∠CAE=30°,
∴∠BAC=90°.
答:∠BAC的度数为90°.
23.【解答】解:(1)S△ABC=?AC?BC=×4×4=8,
故答案为8.
(2)由题意EF2=8,
∴EF=2,
∴正方形EFGH的边长为2.
(3)另一端点对应的数是﹣1+2或﹣1﹣2.
24.【解答】解:(1)设甲队每天修路x米,则乙队每天修路(x﹣50)米,
依题意,得:=,
解得:x=200,
经检验,x=200是原方程的解,且符合题意.
答:甲队每天修路200米.
(2)设乙队需要y天才能完工,
依题意,得:45000﹣(200﹣50)y≥200×120,
解得:y≤140.
答:乙队至少需要140天才能完工.
25.【解答】解:(1)AB==2,
故答案为2.
△ABC是直角三角形.
理由:∵AB=2,AC==,BC=5,
∴AB2+AC2=20+5=25=BC2,
∴∠BAC=90°,
∴△ABC是直角三角形.
(2)如图2中,△DEF即为所求.
(3)如图3中,由题意AB=AR=2,AC=AD=,∠BAC=∠BAR=∠CAD=90°,
∴∠RAD=360°﹣3×90°=90°,
∴S△ADR=?AR?AD=×2×=5.
五、挑战自我(本大题10分)
26.【解答】解:【解决问题】(1)由题意AP=1×1=1(cm),BQ=1×1=1cm,
故答案为1.
(2)∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵AD=PB=3,PA=BQ=1,
∴△ADP≌△BPQ(SAS).
(3)∵△ADP≌△BPQ,
∴∠APD=∠PQB,
∵∠BPQ+∠PQB=90°,
∴∠APD+∠BPQ=90°,
∴∠DPQ=90°,
∴DP⊥PQ.
【变式探究】①当x=1cm/s时,t=1时,两个三角形全等.
②当AP=PB,BQ=AD时,两个三角形全等,
此时t==2,VQ=cm/s,
∴x=cm/s.
综上所述,满足条件的x的值为1或.
同课章节目录
