沪科版八年级下册数学第19章 四边形单元测试卷2解析版
文档属性
| 名称 | 沪科版八年级下册数学第19章 四边形单元测试卷2解析版 |
|
|
| 格式 | zip | ||
| 文件大小 | 497.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览



文档简介
绝密★启用前
四边形单元测试卷
一、单选题(每题4分,共40分)
1.一个多边形内角和是900°,则这个多边形的边数是 ( )
A.7 B.6 C.5 D.4
2.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
3.下列判断正确的是(????)
A.一组对边平行且另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.一组对边平行且有一组对角相等的四边形是平行四边形
D.对角线互相垂直且相等的四边形是正方形
4.如图,的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
5.如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E。若AB=12,BC=20,则线段EF的长为( )
A.2 B.3 C.4 D.5
6.我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线长分别为6和8的菱形,它的中点四边形的对角线长是( )
A.5 B. C.6 D.10
7.如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
A.28° B.56° C.62° D.72°
8.如图,将矩形纸片折叠,使点与点重合,已知,,则折痕BE的长是( ).
A. B. C. D.
9.如图,EF分别是正方形ABCD的边CDAD上的点且CE=DF,AB、BF相交于点O,若S△AOB=10,则S四边形DEOF等于( )
A.5 B.8 C.10 D.12
10.如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题5分,共20分)
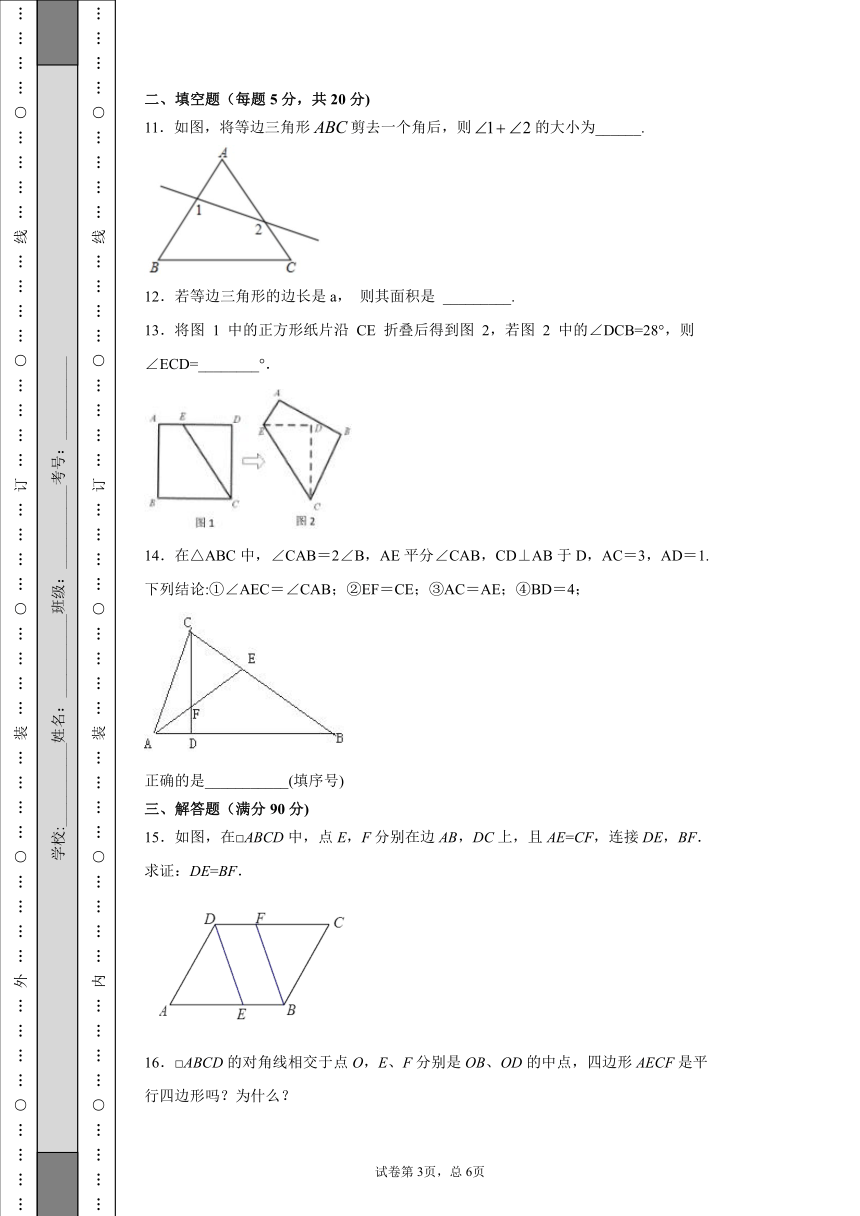
11.如图,将等边三角形剪去一个角后,则的大小为______.
12.若等边三角形的边长是a, 则其面积是 _________.
13.将图 1 中的正方形纸片沿 CE 折叠后得到图 2,若图 2 中的∠DCB=28°,则∠ECD=________°.
14.在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;
正确的是___________(填序号)
三、解答题(满分90分)
15.如图,在□ABCD中,点E,F分别在边AB,DC上,且AE=CF,连接DE,BF.
求证:DE=BF.
16.□ABCD的对角线相交于点O,E、F分别是OB、OD的中点,四边形AECF是平行四边形吗?为什么?
17.如图,在平行四边形ABCD 中,边CD 5 ,对角线 AC 8 , DB 6.
(1)求证:四边形 ABCD 是菱形;
(2)过点 D 作 DH AB 于点 H ,若点 P 是线段 AC 上的一个动点,求 PH PB 的最小.
18.如图,平分,,.
四边形是菱形吗?请说明你的理由;
当满足什么条件时,四边形是正方形,并证明.
19.如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
(1)求证:△ADG≌△FDG;(2)若BG=2AG,BD=2,求AD的长.
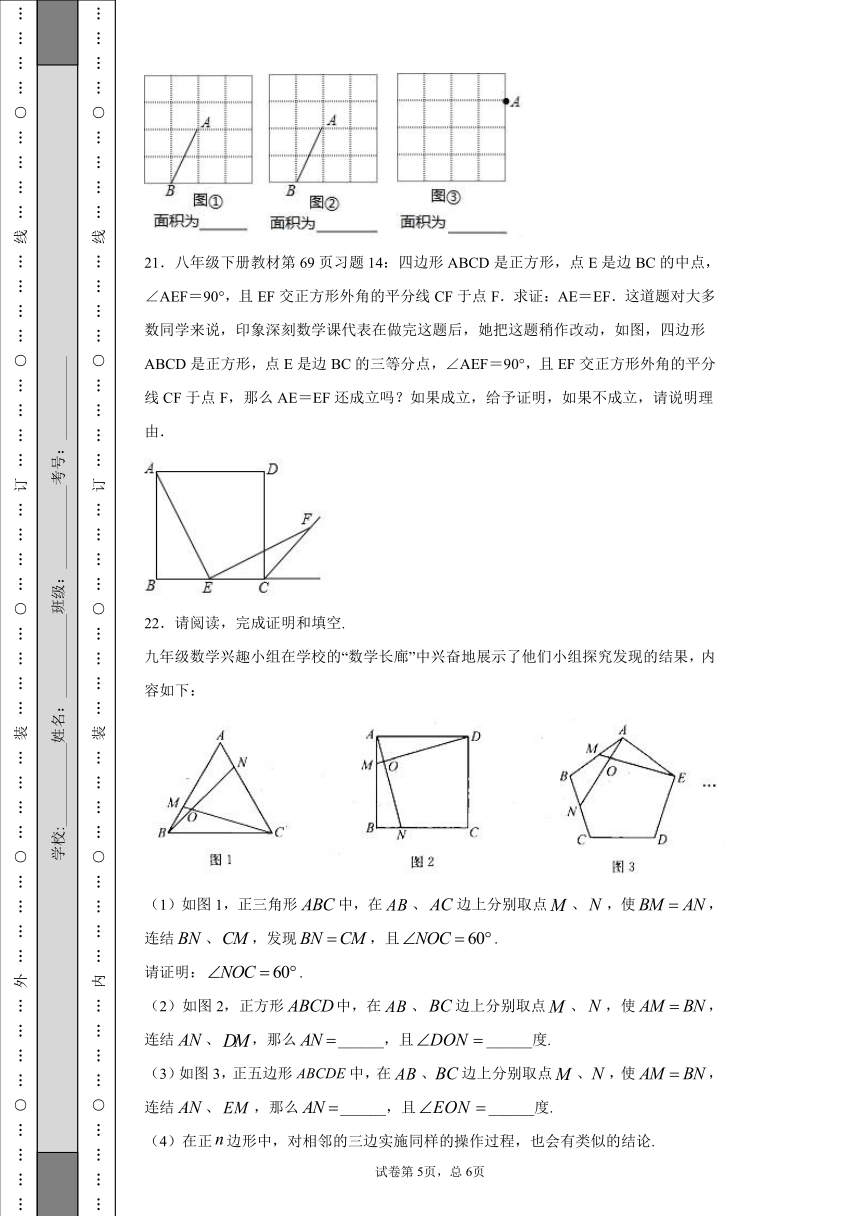
20.图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.
(1)在图①、图②中,以格点为顶点,线段AB为一边,分别画一个平行四边形和菱形,并直接写出它们的面积.(要求两个四边形不全等)
(2)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形,并直接写出它的面积.
21.八年级下册教材第69页习题14:四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由.
22.请阅读,完成证明和填空.
九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,正三角形中,在、边上分别取点、,使,连结、,发现,且.
请证明:.
(2)如图2,正方形中,在、边上分别取点、,使,连结、,那么______,且______度.
(3)如图3,正五边形中,在、边上分别取点、,使,连结、,那么______,且______度.
(4)在正边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.
请大胆猜测,用一句话概括你的发现:________________________________.
23.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,
求证:BE+CF>EF.
小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、BE、FC之间的数量关系?并证明你的猜想.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第6页,总6页
试卷第5页,总6页
参考答案
1.A
【解析】
【分析】
n边形的内角和为(n-2)180°,由此列方程求n的值即可.
【详解】
设这个多边形的边数为n,
则:(n-2)180°=900°,
解得n=7.
故答案为:A.
【点睛】
本题考查了多边形的内角和,熟练掌握该知识点是本题解题的关键.
2.C
【解析】
【分析】
由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
【详解】
解:连结EF,AE与BF交于点O,如图,
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO===4,
∴AE=2AO=8.
故选C.
【点睛】
本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.
3.C
【解析】
【分析】
根据平行四边形、矩形、正方形的判定方法解答即可.
【详解】
选项A,一组对边平行且相等的四边形是平行四边形,选项A错误;
选项B,对角线互相平分且相等的四边形是矩形,选项B错误;
选项C,一组对边平行且有一组对角相等的四边形是平行四边形,选项C正确;
选项D,对角线互相垂直平分且相等的四边形是正方形,选项D错误.
故选C.
【点睛】
本题考查了平行四边形、矩形、正方形的判定方法,熟知平行四边形、矩形、正方形的判定方法是解决本题的关键.
4.A
【解析】
【分析】
利用平行四边形的性质,三角形中位线定理即可解决问题
【详解】
解:平行四边形的周长为18,
,
,,
∴
,
,
,
的周长为,
故选.
【点睛】
本题考查平行四边形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握三角形中位线定理,属于中考常考题型.
5.C
【解析】
【分析】
由直角三角形的性质可求得DF=BD= AB,由角平分线的定义可证得DE∥BC,利用三角形中位线定理可求得DE的长,则可求得EF的长.
【详解】
解:∵AF⊥BF,D为AB的中点,
∴DF=DB=AB=6,
∴∠DBF=∠DFB,
∵BF平分∠ABC,
∴∠DBF=∠CBF,
∴∠DFB=∠CBF,
∴DE∥BC,
∴DE为△ABC的中位线,
∴DE=BC=10,
∴EF=DE?DF=10?6=4,
故选:C.
【点睛】
本题考查直角三角形斜边上的中线的性质,角平分线的性质,等腰三角形的判定与性质,三角形中位线定理.根据直角三角形斜边上的中线是斜边是斜边的一半可得△DBF为等腰三角形,通过角平分线的性质和等角对等边可得DF//BC,即DE为△ABC的中位线,从而计算出DE,继而求出EF.
6.A
【解析】
【分析】
顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,问题得解.
【详解】
∵顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形;
理由如下:∵E、F、G、H分别为各边中点
∴EF∥GH∥AC,EF=GH= DB,
EF=HG=AC,EH∥FG∥BD
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形,
∵EH=BD=3cm,EF=AC=4cm,
∴HF=cm.
故答案为:A.
【点睛】
本题考查菱形的性质,菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半以及勾股定理的运用.
7.C
【解析】
【分析】
根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
【详解】
解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°-28°=62°.
故选:C.
【点睛】
本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.
8.D
【解析】
【分析】
先过点F作FM⊥BC于M.利用勾股定理可求出AE,再利用翻折变换的知识,可得到AE=CE,∠AEF=∠CEF,再利用平行线可得∠AEF=∠AFE,故有AE=AF,设BE=x,根据题意得到x2+42=(8-x)2,解方程即可.
【详解】
过点F作FM⊥BC于GM,
∵EF是直角梯形AECD的折痕
∴AE=CE,∠AEF=∠CEF.
又∵AD∥BC,
∴∠AFE=∠FEM,
根据翻折不变性,∠AEF=∠FEM,
∴∠AFE=∠AEF,
∴AE=AF.
在Rt△ABE中,设BE=x,AB=4,AE=CE=8-x.x2+42=(8-x)2解得x=3.
∴BE=3.
故选:D.
【点睛】
考查了折叠的知识,矩形的性质,勾股定理等知识点的理解和运用,关键是根据题意得出方程x2+42=(8-x)2.
9.C
【解析】
【分析】
根据全等三角形的面积相等可得S△ABF=S△ADE然后都减去△AOF的面积,即可得解
【详解】
在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,∴AD-DF=CD-CE,即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE,∴S△ABF=S△DAE,∴S△ABF-S△AOF=S△DAE-S△AOF,即S△AOB=S四边形DEOF=10,故选C.
【点睛】
此题考查全等三角形的判定与性质和正方形的性质,解题关键在于利用三角形全等求证
10.C
【解析】
试题分析:由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S?ABCD=AB?AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB<OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,且BD>BC,
∴AB<OB,故③错误;
∵CE=BE,CO=OA,
∴OE=AB,
∴OE=BC,故④正确.
故选C.
11.
【解析】
【分析】
根据等边三角形的性质求出∠B、∠C的度数,再根据四边形的内角和定理求出∠1+∠2的大小.
【详解】
∵△ABC为等边三角形,
∴∠B+∠C=60°+60°=120°,
根据四边形内角和为360°,
可知∠1+∠2=360°?120°=240°.
故答案为:240°.
【点睛】
本题考查了等边三角形的性质以及四边形内角和,熟练掌握等边三角形每个内角为60°,以及四边形内角和为360°是解题的关键.
12.
【解析】
分析:根据等边三角形的性质,作出一边上的高后出现了一个直角三角形,斜边为a,一条直角边为,由勾股定理可求出另一条直角边即高的长度,然后再算面积.
详解:如图所示,过A作AD⊥BC于D,则BD=CD=.
在Rt△ACD中,AC=a,CD=,∴AC2=AD2+CD2.
∴AD2=AC2-CD2=a2-()2=a2,AD=a.
∴S△ABC=AD·BC=×a·a=a2.
故答案为:a2.
点睛:本题主要者查勾股定理及等腰三角形的性质,正确的画出相关的图形,构造直角三角形是解题关键.
13.见解析
【解析】
【分析】
根据折叠的性质知2∠ECD+∠DCB=90°,再由∠DCB=28°,可得2∠ECD=62°,进而求解.
【详解】
由折叠的性质可得:2∠ECD+∠DCB=90°,
∵∠DCB=28°, ∴2∠ECD=90°-28°=62°,
∴∠ECD=31°,故答案为:31.
【点睛】
本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
14.①②.
【解析】
【分析】
根据角平分线,三角形的外角性质以及等角对等边的性质可得出结论①②正确.
【详解】
解:∵AE平分∠CAB,
∴∠CAB=2∠EAB,
∵∠CAB=2∠B,
∴∠EAB=∠B,
∵∠AEC=∠B+∠EAB,
∴∠AEC=2∠B=∠CAB,①正确;
∵CD⊥AB于D,
∴∠B+∠DCB=90°,∠EAB+∠AFD=90°,
∵∠EAB=∠B,
∴∠DCB=∠AFD,
∵∠CFE=∠AFD,
∴∠CFE=∠DCB,
∴EF=CE,②正确;
无法证明AC=AE,故③不正确;
∵AC=3,AD=1,CD⊥AB于D,
∴CD= ,
不能得出BD=4,故④不正确.
故答案为①②.
【点睛】
本题考查角平分线,三角形的外角性质以及等角对等边的性质,正确的识别图形是解题的关键.
15.详见解析
【解析】
【分析】
欲证明,只要证明≌即可.由四边形ABCD是平行四边形,
可证,,从而根据“SAS”可证明≌.
【详解】
证明:四边形ABCD是平行四边形,
,,
在和中,
,
≌,
.
【点睛】
本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
16.结论:四边形AECF是平行四边形,理由见解析.
【解析】
【分析】
证明AC和EF互相平分即可证得四边形AECF是平行四边形.
【详解】
结论:四边形AECF是平行四边形
理由是:∵ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵E,F分别是OB、OD的中点,
∴OA=OC,OE=OF,
∴四边形AECF是平行四边形.
【点睛】
本题考查了平行四边形的性质和判定,解题的关键是熟练掌握平行四边形的性质和判定.
17.(1)见解析;(2)PH PB最小值为9.6.
【解析】
【分析】
(1)根据平行四边形的性质可得OD=BD,OC=AC,利用勾股定理的逆定理可证△OCD为直角三角形,即∠COD=90°,再根据菱形的判定定理即可得证;
(2)由菱形的性质可得B点关于AC的对称点是点D,则DH即为PH+PB的最小值,利用菱形的面积公式即可求得DH的长.
【详解】
(1)∵四边形ABCD为平行四边形,
∴OD=BD=3,OC=AC=4,
∵,
∴∠COD=90°,
∴AC与BD互相垂直平分,
∴四边形ABCD为菱形;
(2)∵BD⊥AC,OB=OD,
∴DH即为PH+PB的最小值,
∵S菱形ABCD=AC·BD=DH·AB,
∴6×8=5·DH,
解得DH=9.6.
【点睛】
本题主要考查菱形的判定与性质,菱形的面积公式,最短路径问题,解此题的关键在于熟练掌握其知识点.
18.四边形是菱形,理由见解析;(2)当时,四边形是正方形,理由见解析
【解析】
【分析】
(1)首先证明四边形AEDF是平行四边形,然后再利用AD平分∠A证明AF=DF可得四边形AEDF是菱形;
(2)当∠BAC=90°时,四边形AEDF是正方形,根据有一个角是直角的菱形是正方形可证.
【详解】
解:四边形是菱形.
∵,,
∴四边形是平行四边形;
∵平分,
∴,
∵,
∴,
∴,
∴,
∴四边形是菱形;
当时,四边形是正方形;
∵四边形是菱形,,
∴四边形是正方形.
【点睛】
此题主要考查了菱形和正方形的判定,关键是掌握一组邻边相等的平行四边形是菱形.
19.(1)证明见解析;(2)AD=.
【解析】
试题分析:(1)由矩形的性质和已知条件得出∠A=∠GFD,∠ADG=∠FDG,由AAS即可证明△AGD≌△FGD;
(2)由△AGD≌△FGD,得出对应边相等FG=AG,根据BG=2AG求出∠FBG=30°,根据直角三角形中30° 的角所对的边是斜边的一半即可求出.
试题解析:
(1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=∠DFG=90°,
又∠ADG=∠FDG,DG=DG,
∴△ADG≌△FDG.
(2)解:由(1)得△ADG≌△FDG,
∴FG=AG,
∵BG=2AG,∴BG=2FG,
∴在Rt△BFG中,sin∠FBG=,
∴∠FBG=30°,
∴AD=.
20.(1)画图见解析,菱形的面积=4;平行四边形的面积=4;(2)画图见解析,面积为10.
【解析】
【分析】
(1)根据菱形和平行四边形的画法解答即可;
(2)根据勾股定理逆定理,结合网格结构,作出最长的线段作为正方形的边长即可.
【详解】
(1)如图①②所示:
菱形的面积=4;平行四边形的面积=4;
(2)如图③所示:
正方形的面积=10;
【点睛】
本题考查了作图﹣应用与设计作图.熟记勾股定理,菱形、平行四边形的性质以及正方形的性质是解题的关键所在.
21.成立,理由见解析.
【解析】
【分析】
取AB的三等分点,连接GE,由点E是边BC的三等分点,得到BE=BG,根据正方形的性质得到AG=EC,根据全等三角形的性质即可得到结论.
【详解】
证明:取AB的三等分点,连接GE,
∵点E是边BC的三等分点,
∴BE=BG,
∵四边形ABCD是正方形,
∴AG=EC,
∵△EBG为等腰直角三角形,可知∠AGE=135°,
∵∠AEF=90°,
∠BEA+∠FEC=90°,
∠BEA+∠BAE=90°,
∴∠BAE=∠FEC.
∴△AGE≌△ECF(ASA),
∴AE=EF.
【点睛】
此题考查正方形的性质,三角形全等的判定与性质,角平分线的性质等知识点,注意结合图形,灵活作出辅助线解决问题.
22.(1)见解析;(2)DM,90°;(3)EM,108°;(4)见解析.
【解析】
【分析】
①以正n边形的性质(即各边相等,各内角相等)为切入点,构造与 全等的三角形;②通过对正三角形的探究与分析,得到正n边形的一般性结论,即所探究的角恰好等于正n边形的内角.
【详解】
解 (1)证明:∵是正三角形,∴,.在和中,,∴.∴.又∵,∴.又∵,∴.
(2)在正方形中,,.
(3)在正五边形中,,.
(4)所连结的两条线段相等,所求的角恰好等于正边形的内角.
【点睛】
本题以正多边形为背景,以正三角形ABC为切入点,通过对问题的类比、改造、延伸和拓展来检测分析问题、解决问题的能力.启示我们学习数学要在“做数学”,而不是“背数学”.
23.EF2=AE2+CF2,,详见解析
【解析】
【分析】
猜想:EF2=AE2+CF2,延长EO交CD于点H,连结FH,首先证明△AEO≌△CHO,进而可得EO=HO,CH=AE,由折叠的性质可得△EFO≌△EFB,所以∠EOF=∠B=90°,继而在△FCH中,由勾股定理得FH2=CH2+FC2,即EF2=AE2+CF2问题得证.
【详解】
解:猜想:EF2=AE2+CF2,
理由如下:延长EO交CD于点H,连结FH.
∵四边形ABCD是矩形.
∴AB∥DC.∠B=90°
∴∠EAO=∠HCO.
∵O为对角线AC中点,
∴AO=CO.
∵∠BOE=∠COH,
∴△AEO≌△CHO.
∴EO=HO,CH=AE,
由题意可知△EFO≌△EFB.
∴∠EOF=∠B=90°.
∴OF垂直平分EH.
∴FH=EF
在△FCH中,由勾股定理得FH2=CH2+FC2,
∴EF2=AE2+CF2.
【点睛】
考点:全等三角形的判定与性质;勾股定理;矩形的性质
答案第2页,总17页
答案第5页,总17页
四边形单元测试卷
一、单选题(每题4分,共40分)
1.一个多边形内角和是900°,则这个多边形的边数是 ( )
A.7 B.6 C.5 D.4
2.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
3.下列判断正确的是(????)
A.一组对边平行且另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.一组对边平行且有一组对角相等的四边形是平行四边形
D.对角线互相垂直且相等的四边形是正方形
4.如图,的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
5.如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E。若AB=12,BC=20,则线段EF的长为( )
A.2 B.3 C.4 D.5
6.我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线长分别为6和8的菱形,它的中点四边形的对角线长是( )
A.5 B. C.6 D.10
7.如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
A.28° B.56° C.62° D.72°
8.如图,将矩形纸片折叠,使点与点重合,已知,,则折痕BE的长是( ).
A. B. C. D.
9.如图,EF分别是正方形ABCD的边CDAD上的点且CE=DF,AB、BF相交于点O,若S△AOB=10,则S四边形DEOF等于( )
A.5 B.8 C.10 D.12
10.如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题5分,共20分)
11.如图,将等边三角形剪去一个角后,则的大小为______.
12.若等边三角形的边长是a, 则其面积是 _________.
13.将图 1 中的正方形纸片沿 CE 折叠后得到图 2,若图 2 中的∠DCB=28°,则∠ECD=________°.
14.在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;
正确的是___________(填序号)
三、解答题(满分90分)
15.如图,在□ABCD中,点E,F分别在边AB,DC上,且AE=CF,连接DE,BF.
求证:DE=BF.
16.□ABCD的对角线相交于点O,E、F分别是OB、OD的中点,四边形AECF是平行四边形吗?为什么?
17.如图,在平行四边形ABCD 中,边CD 5 ,对角线 AC 8 , DB 6.
(1)求证:四边形 ABCD 是菱形;
(2)过点 D 作 DH AB 于点 H ,若点 P 是线段 AC 上的一个动点,求 PH PB 的最小.
18.如图,平分,,.
四边形是菱形吗?请说明你的理由;
当满足什么条件时,四边形是正方形,并证明.
19.如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
(1)求证:△ADG≌△FDG;(2)若BG=2AG,BD=2,求AD的长.
20.图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.
(1)在图①、图②中,以格点为顶点,线段AB为一边,分别画一个平行四边形和菱形,并直接写出它们的面积.(要求两个四边形不全等)
(2)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形,并直接写出它的面积.
21.八年级下册教材第69页习题14:四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由.
22.请阅读,完成证明和填空.
九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,正三角形中,在、边上分别取点、,使,连结、,发现,且.
请证明:.
(2)如图2,正方形中,在、边上分别取点、,使,连结、,那么______,且______度.
(3)如图3,正五边形中,在、边上分别取点、,使,连结、,那么______,且______度.
(4)在正边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.
请大胆猜测,用一句话概括你的发现:________________________________.
23.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,
求证:BE+CF>EF.
小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、BE、FC之间的数量关系?并证明你的猜想.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校
:___________
姓名:
___________
班级:
___________
考号:
___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第6页,总6页
试卷第5页,总6页
参考答案
1.A
【解析】
【分析】
n边形的内角和为(n-2)180°,由此列方程求n的值即可.
【详解】
设这个多边形的边数为n,
则:(n-2)180°=900°,
解得n=7.
故答案为:A.
【点睛】
本题考查了多边形的内角和,熟练掌握该知识点是本题解题的关键.
2.C
【解析】
【分析】
由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
【详解】
解:连结EF,AE与BF交于点O,如图,
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO===4,
∴AE=2AO=8.
故选C.
【点睛】
本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.
3.C
【解析】
【分析】
根据平行四边形、矩形、正方形的判定方法解答即可.
【详解】
选项A,一组对边平行且相等的四边形是平行四边形,选项A错误;
选项B,对角线互相平分且相等的四边形是矩形,选项B错误;
选项C,一组对边平行且有一组对角相等的四边形是平行四边形,选项C正确;
选项D,对角线互相垂直平分且相等的四边形是正方形,选项D错误.
故选C.
【点睛】
本题考查了平行四边形、矩形、正方形的判定方法,熟知平行四边形、矩形、正方形的判定方法是解决本题的关键.
4.A
【解析】
【分析】
利用平行四边形的性质,三角形中位线定理即可解决问题
【详解】
解:平行四边形的周长为18,
,
,,
∴
,
,
,
的周长为,
故选.
【点睛】
本题考查平行四边形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握三角形中位线定理,属于中考常考题型.
5.C
【解析】
【分析】
由直角三角形的性质可求得DF=BD= AB,由角平分线的定义可证得DE∥BC,利用三角形中位线定理可求得DE的长,则可求得EF的长.
【详解】
解:∵AF⊥BF,D为AB的中点,
∴DF=DB=AB=6,
∴∠DBF=∠DFB,
∵BF平分∠ABC,
∴∠DBF=∠CBF,
∴∠DFB=∠CBF,
∴DE∥BC,
∴DE为△ABC的中位线,
∴DE=BC=10,
∴EF=DE?DF=10?6=4,
故选:C.
【点睛】
本题考查直角三角形斜边上的中线的性质,角平分线的性质,等腰三角形的判定与性质,三角形中位线定理.根据直角三角形斜边上的中线是斜边是斜边的一半可得△DBF为等腰三角形,通过角平分线的性质和等角对等边可得DF//BC,即DE为△ABC的中位线,从而计算出DE,继而求出EF.
6.A
【解析】
【分析】
顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,问题得解.
【详解】
∵顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形;
理由如下:∵E、F、G、H分别为各边中点
∴EF∥GH∥AC,EF=GH= DB,
EF=HG=AC,EH∥FG∥BD
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形,
∵EH=BD=3cm,EF=AC=4cm,
∴HF=cm.
故答案为:A.
【点睛】
本题考查菱形的性质,菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半以及勾股定理的运用.
7.C
【解析】
【分析】
根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
【详解】
解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°-28°=62°.
故选:C.
【点睛】
本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.
8.D
【解析】
【分析】
先过点F作FM⊥BC于M.利用勾股定理可求出AE,再利用翻折变换的知识,可得到AE=CE,∠AEF=∠CEF,再利用平行线可得∠AEF=∠AFE,故有AE=AF,设BE=x,根据题意得到x2+42=(8-x)2,解方程即可.
【详解】
过点F作FM⊥BC于GM,
∵EF是直角梯形AECD的折痕
∴AE=CE,∠AEF=∠CEF.
又∵AD∥BC,
∴∠AFE=∠FEM,
根据翻折不变性,∠AEF=∠FEM,
∴∠AFE=∠AEF,
∴AE=AF.
在Rt△ABE中,设BE=x,AB=4,AE=CE=8-x.x2+42=(8-x)2解得x=3.
∴BE=3.
故选:D.
【点睛】
考查了折叠的知识,矩形的性质,勾股定理等知识点的理解和运用,关键是根据题意得出方程x2+42=(8-x)2.
9.C
【解析】
【分析】
根据全等三角形的面积相等可得S△ABF=S△ADE然后都减去△AOF的面积,即可得解
【详解】
在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,∴AD-DF=CD-CE,即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE,∴S△ABF=S△DAE,∴S△ABF-S△AOF=S△DAE-S△AOF,即S△AOB=S四边形DEOF=10,故选C.
【点睛】
此题考查全等三角形的判定与性质和正方形的性质,解题关键在于利用三角形全等求证
10.C
【解析】
试题分析:由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S?ABCD=AB?AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB<OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,且BD>BC,
∴AB<OB,故③错误;
∵CE=BE,CO=OA,
∴OE=AB,
∴OE=BC,故④正确.
故选C.
11.
【解析】
【分析】
根据等边三角形的性质求出∠B、∠C的度数,再根据四边形的内角和定理求出∠1+∠2的大小.
【详解】
∵△ABC为等边三角形,
∴∠B+∠C=60°+60°=120°,
根据四边形内角和为360°,
可知∠1+∠2=360°?120°=240°.
故答案为:240°.
【点睛】
本题考查了等边三角形的性质以及四边形内角和,熟练掌握等边三角形每个内角为60°,以及四边形内角和为360°是解题的关键.
12.
【解析】
分析:根据等边三角形的性质,作出一边上的高后出现了一个直角三角形,斜边为a,一条直角边为,由勾股定理可求出另一条直角边即高的长度,然后再算面积.
详解:如图所示,过A作AD⊥BC于D,则BD=CD=.
在Rt△ACD中,AC=a,CD=,∴AC2=AD2+CD2.
∴AD2=AC2-CD2=a2-()2=a2,AD=a.
∴S△ABC=AD·BC=×a·a=a2.
故答案为:a2.
点睛:本题主要者查勾股定理及等腰三角形的性质,正确的画出相关的图形,构造直角三角形是解题关键.
13.见解析
【解析】
【分析】
根据折叠的性质知2∠ECD+∠DCB=90°,再由∠DCB=28°,可得2∠ECD=62°,进而求解.
【详解】
由折叠的性质可得:2∠ECD+∠DCB=90°,
∵∠DCB=28°, ∴2∠ECD=90°-28°=62°,
∴∠ECD=31°,故答案为:31.
【点睛】
本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
14.①②.
【解析】
【分析】
根据角平分线,三角形的外角性质以及等角对等边的性质可得出结论①②正确.
【详解】
解:∵AE平分∠CAB,
∴∠CAB=2∠EAB,
∵∠CAB=2∠B,
∴∠EAB=∠B,
∵∠AEC=∠B+∠EAB,
∴∠AEC=2∠B=∠CAB,①正确;
∵CD⊥AB于D,
∴∠B+∠DCB=90°,∠EAB+∠AFD=90°,
∵∠EAB=∠B,
∴∠DCB=∠AFD,
∵∠CFE=∠AFD,
∴∠CFE=∠DCB,
∴EF=CE,②正确;
无法证明AC=AE,故③不正确;
∵AC=3,AD=1,CD⊥AB于D,
∴CD= ,
不能得出BD=4,故④不正确.
故答案为①②.
【点睛】
本题考查角平分线,三角形的外角性质以及等角对等边的性质,正确的识别图形是解题的关键.
15.详见解析
【解析】
【分析】
欲证明,只要证明≌即可.由四边形ABCD是平行四边形,
可证,,从而根据“SAS”可证明≌.
【详解】
证明:四边形ABCD是平行四边形,
,,
在和中,
,
≌,
.
【点睛】
本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
16.结论:四边形AECF是平行四边形,理由见解析.
【解析】
【分析】
证明AC和EF互相平分即可证得四边形AECF是平行四边形.
【详解】
结论:四边形AECF是平行四边形
理由是:∵ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵E,F分别是OB、OD的中点,
∴OA=OC,OE=OF,
∴四边形AECF是平行四边形.
【点睛】
本题考查了平行四边形的性质和判定,解题的关键是熟练掌握平行四边形的性质和判定.
17.(1)见解析;(2)PH PB最小值为9.6.
【解析】
【分析】
(1)根据平行四边形的性质可得OD=BD,OC=AC,利用勾股定理的逆定理可证△OCD为直角三角形,即∠COD=90°,再根据菱形的判定定理即可得证;
(2)由菱形的性质可得B点关于AC的对称点是点D,则DH即为PH+PB的最小值,利用菱形的面积公式即可求得DH的长.
【详解】
(1)∵四边形ABCD为平行四边形,
∴OD=BD=3,OC=AC=4,
∵,
∴∠COD=90°,
∴AC与BD互相垂直平分,
∴四边形ABCD为菱形;
(2)∵BD⊥AC,OB=OD,
∴DH即为PH+PB的最小值,
∵S菱形ABCD=AC·BD=DH·AB,
∴6×8=5·DH,
解得DH=9.6.
【点睛】
本题主要考查菱形的判定与性质,菱形的面积公式,最短路径问题,解此题的关键在于熟练掌握其知识点.
18.四边形是菱形,理由见解析;(2)当时,四边形是正方形,理由见解析
【解析】
【分析】
(1)首先证明四边形AEDF是平行四边形,然后再利用AD平分∠A证明AF=DF可得四边形AEDF是菱形;
(2)当∠BAC=90°时,四边形AEDF是正方形,根据有一个角是直角的菱形是正方形可证.
【详解】
解:四边形是菱形.
∵,,
∴四边形是平行四边形;
∵平分,
∴,
∵,
∴,
∴,
∴,
∴四边形是菱形;
当时,四边形是正方形;
∵四边形是菱形,,
∴四边形是正方形.
【点睛】
此题主要考查了菱形和正方形的判定,关键是掌握一组邻边相等的平行四边形是菱形.
19.(1)证明见解析;(2)AD=.
【解析】
试题分析:(1)由矩形的性质和已知条件得出∠A=∠GFD,∠ADG=∠FDG,由AAS即可证明△AGD≌△FGD;
(2)由△AGD≌△FGD,得出对应边相等FG=AG,根据BG=2AG求出∠FBG=30°,根据直角三角形中30° 的角所对的边是斜边的一半即可求出.
试题解析:
(1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=∠DFG=90°,
又∠ADG=∠FDG,DG=DG,
∴△ADG≌△FDG.
(2)解:由(1)得△ADG≌△FDG,
∴FG=AG,
∵BG=2AG,∴BG=2FG,
∴在Rt△BFG中,sin∠FBG=,
∴∠FBG=30°,
∴AD=.
20.(1)画图见解析,菱形的面积=4;平行四边形的面积=4;(2)画图见解析,面积为10.
【解析】
【分析】
(1)根据菱形和平行四边形的画法解答即可;
(2)根据勾股定理逆定理,结合网格结构,作出最长的线段作为正方形的边长即可.
【详解】
(1)如图①②所示:
菱形的面积=4;平行四边形的面积=4;
(2)如图③所示:
正方形的面积=10;
【点睛】
本题考查了作图﹣应用与设计作图.熟记勾股定理,菱形、平行四边形的性质以及正方形的性质是解题的关键所在.
21.成立,理由见解析.
【解析】
【分析】
取AB的三等分点,连接GE,由点E是边BC的三等分点,得到BE=BG,根据正方形的性质得到AG=EC,根据全等三角形的性质即可得到结论.
【详解】
证明:取AB的三等分点,连接GE,
∵点E是边BC的三等分点,
∴BE=BG,
∵四边形ABCD是正方形,
∴AG=EC,
∵△EBG为等腰直角三角形,可知∠AGE=135°,
∵∠AEF=90°,
∠BEA+∠FEC=90°,
∠BEA+∠BAE=90°,
∴∠BAE=∠FEC.
∴△AGE≌△ECF(ASA),
∴AE=EF.
【点睛】
此题考查正方形的性质,三角形全等的判定与性质,角平分线的性质等知识点,注意结合图形,灵活作出辅助线解决问题.
22.(1)见解析;(2)DM,90°;(3)EM,108°;(4)见解析.
【解析】
【分析】
①以正n边形的性质(即各边相等,各内角相等)为切入点,构造与 全等的三角形;②通过对正三角形的探究与分析,得到正n边形的一般性结论,即所探究的角恰好等于正n边形的内角.
【详解】
解 (1)证明:∵是正三角形,∴,.在和中,,∴.∴.又∵,∴.又∵,∴.
(2)在正方形中,,.
(3)在正五边形中,,.
(4)所连结的两条线段相等,所求的角恰好等于正边形的内角.
【点睛】
本题以正多边形为背景,以正三角形ABC为切入点,通过对问题的类比、改造、延伸和拓展来检测分析问题、解决问题的能力.启示我们学习数学要在“做数学”,而不是“背数学”.
23.EF2=AE2+CF2,,详见解析
【解析】
【分析】
猜想:EF2=AE2+CF2,延长EO交CD于点H,连结FH,首先证明△AEO≌△CHO,进而可得EO=HO,CH=AE,由折叠的性质可得△EFO≌△EFB,所以∠EOF=∠B=90°,继而在△FCH中,由勾股定理得FH2=CH2+FC2,即EF2=AE2+CF2问题得证.
【详解】
解:猜想:EF2=AE2+CF2,
理由如下:延长EO交CD于点H,连结FH.
∵四边形ABCD是矩形.
∴AB∥DC.∠B=90°
∴∠EAO=∠HCO.
∵O为对角线AC中点,
∴AO=CO.
∵∠BOE=∠COH,
∴△AEO≌△CHO.
∴EO=HO,CH=AE,
由题意可知△EFO≌△EFB.
∴∠EOF=∠B=90°.
∴OF垂直平分EH.
∴FH=EF
在△FCH中,由勾股定理得FH2=CH2+FC2,
∴EF2=AE2+CF2.
【点睛】
考点:全等三角形的判定与性质;勾股定理;矩形的性质
答案第2页,总17页
答案第5页,总17页
