2.5 一元一次不等式与一次函数课件(31张PPT)
文档属性
| 名称 | 2.5 一元一次不等式与一次函数课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
数学北师大版
八年级
2.5一元一次不等式与一次函数
复习巩固
一元一次方程与一次函数有什么关系?
A
1.一元一次方程2x+1=0的解是( )
A.x=-2
D.x=2
B.x=-
C.x=
2.直线y=-2x+1与x轴的交点坐标为( )
A. (0,1)
B.(0,-1)
C.( ,0)
D.(- ,0)
3.直线y=-2x+1与y轴的交点坐标为( )
A. (0,1)
B.(0,-1)
C.( ,0)
D. (- ,0)
C
C
6.如图,是一次函数y=kx+b(k≠0)的图象
方程kx+b=0的解是________;
x=6
4.-元一次不等式-2x+1>0的解集是( )
A.x>1
B.x>
C.x<1
D.x<
5.自变量x取何值时,函数y=-2x+1的值大于0? ( )
A.x>1
B.x>
C.x<1.
D.x<
D
D
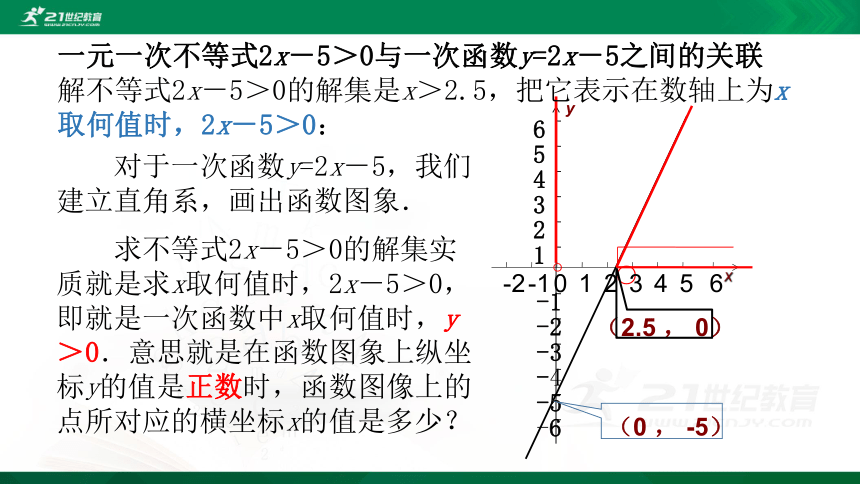
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联数
一次函数y=2x-5研究的是横坐标与纵坐标的取值问题,即(x,y),有时会遇到横坐标x取哪些值时纵坐标y>0的问题;而当y>0时,有不等式2x-5>0.
不等式2x-5>0研究的是x取哪些值时,2x-5>0成立. 因为y=2x-5,所以x取哪些值时, 2x-5>0成立的问题就是x取哪些值时, y>0 成立的问题.
x
○
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
(2.5 , 0)
y
对于一次函数y=2x-5,我们建立直角系,画出函数图象.
(0 , -5)
求不等式2x-5>0的解集实质就是求x取何值时,2x-5>0,即就是一次函数中x取何值时,y>0.意思就是在函数图象上纵坐标y的值是正数时,函数图像上的点所对应的横坐标x的值是多少?
○
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联
解不等式2x-5>0的解集是x>2.5,把它表示在数轴上为x取何值时,2x-5>0:
x
○
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
(2.5 , 0)
y
(0 , -5)
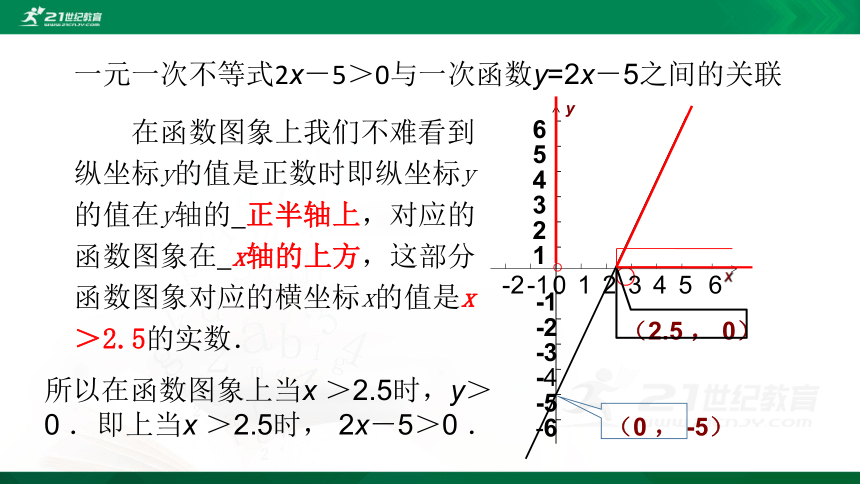
在函数图象上我们不难看到纵坐标y的值是正数时即纵坐标y的值在y轴的 正半轴上,对应的函数图象在 x轴的上方,这部分函数图象对应的横坐标x的值是x >2.5的实数.
所以在函数图象上当x >2.5时,y>0 .即上当x >2.5时, 2x-5>0 .
○
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联
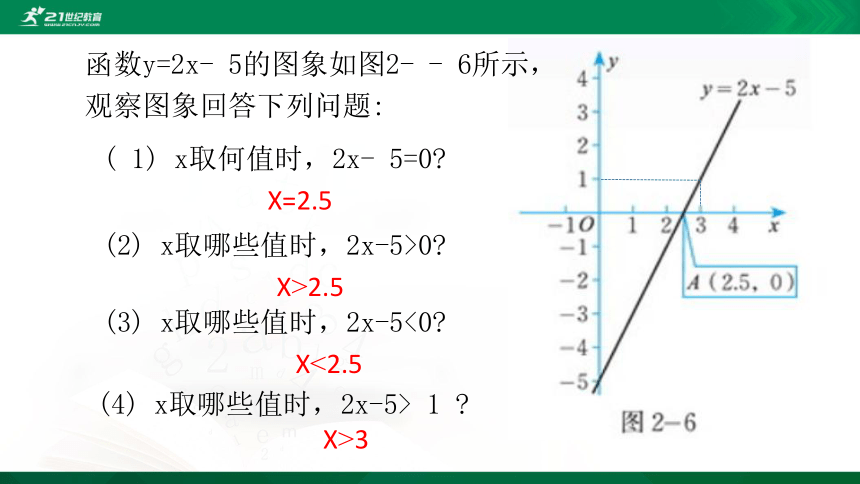
函数y=2x- 5的图象如图2- - 6所示,观察图象回答下列问题:
( 1) x取何值时,2x- 5=0?
(2) x取哪些值时,2x-5>0?
(3) x取哪些值时,2x-5<0?
(4) x取哪些值时,2x-5> 1 ?
X=2.5
X>2.5
X<2.5
X>3
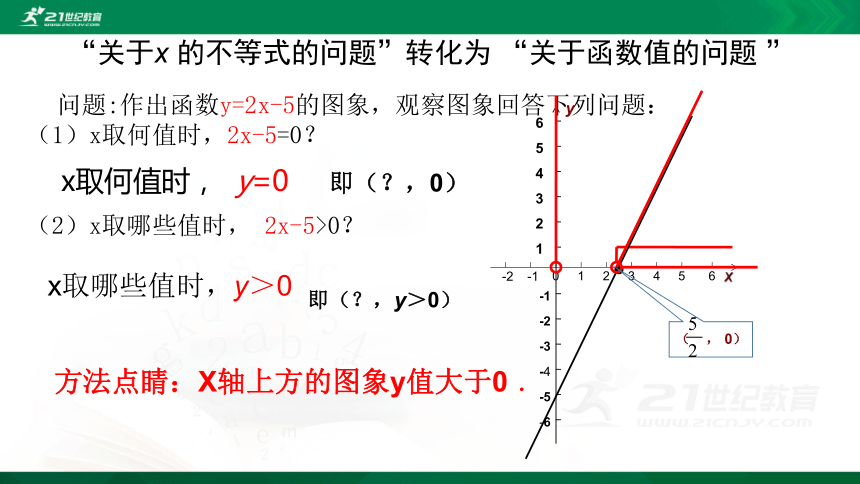
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
问题:作出函数y=2x-5的图象,观察图象回答下列问题:
(1)x取何值时,2x-5=0?
(2)x取哪些值时, 2x-5>0?
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
x取何值时, y=0
即(?,0)
x取哪些值时,y>0
即(?,y>0)
( , 0)
方法点睛:X轴上方的图象y值大于0 .
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
问题:
作出函数y=2x-5的图象,观察图象回答下列问题:
(3)x取哪些值时, 2x-5<0?
x取哪些值时, y<0
即(?,y <0)
在函数图象上我们不难看到纵坐标y的值是负数时,纵坐标y的值在y轴的负半轴上,对应的函数图象在x轴的下方,这部分函数图象对应的横坐标x的值是x<2.5 的实数.
意思就是在函数图象上纵坐标y的值是负数时,函数图像上的点所对应的横坐标x的值是多少?
问题:作出函数y=2x-5的图象,观察图象回答下列问题:
(4)x取哪些值时, 2x-5>3?
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
x取哪些值时, y>3
即(?,y>3)
意思就是在函数图象上纵坐标y的值大于3时,函数图像上的点所对应的横坐标x的值是多少?
过纵坐标为3的点作一条直线平行于x轴这条直线,与y=2x-5相交于点(4 , 3),在函数图象上我们不难看到纵坐标y的值大于3时,纵坐标y的值在y轴上大于3 以上的部分,对应的函数图象在直线y=3的上方,这部分函数图象对应的横坐标x的值是x >4的实数.
(4 , 3)
想一想:
如果y=-2x-5,
那么当x取何
值时,y>0?
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
0
1
2
3
4
x
-5
y
y=-2x-5
解:由图可知,当x<-2.5时,y>0
由上述讨论易知:
函数、(方程) 不等式
“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ;
反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”
因此,
我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与函数 、方程是紧密联系着
的一个整体 。
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集.
(1)3x+6>0
(3)–x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4)–x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
练习:利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
做一做:
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
x
-2
0
10
8
6
4
2
100
90
80
70
60
50
40
30
20
10
/s
y/m
y
y
y
y
哥
哥
弟
弟
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
9秒
前9秒
9秒后
弟
哥
随堂练习:
已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2,你是怎样做的?与同伴交流。
x<2
例2、解不等式5x+4<2x+10 .
解法1:原不等式化为3x -6<0,
画出直线y = 3x -6(如图)
所以不等式的解集为x<2 .
函数图象法:
解不等式法:
解法2:画出直线y1 = 5x +4
y2 = 2x +10
x
y
0
2
y2=2x+10
y1=5x+4
y1 <y2
5x+4<2x+10
3x -6<0,
y<0
所以不等式的解集为x<2 .
本节知识归纳
课外作业
3.某单位计划10月份组织员工到外地旅游,估计人数在6~15之间.甲、乙两旅行社的服务质量相同,且对外报价都是200元,该单位联系时,甲旅行社表示可给予每位游客八折;乙旅行社表示,可先免去一位游客的旅游费用,其余游客九折. (1)分别写出两旅行社所报旅游费用y与人数x的函数关系式. (2)若有11人参加旅游,则应选择哪个旅行社? (3)当人数为多少时可随意选择?
解:(1)由题意,得 甲:y=200x×80%=160x; 乙:y=200×(x-1)×90%=180x-180. (2)当x=11时, 甲:y=160×11=1 760(元); 乙:y=180×11-180=1 800(元). ∵1 760<1 800,∴甲旅行社所报旅游费用少些,应选甲旅行社.
(3)由题意,得160x=180x-180, 解得x=9. 所以当人数为9时,两家旅行社的费用相同,可随意选择.
3.某单位计划10月份组织员工到外地旅游,估计人数在6~15之间.甲、乙两旅行社的服务质量相同,且对外报价都是200元,该单位联系时,甲旅行社表示可给予每位游客八折;乙旅行社表示,可先免去一位游客的旅游费用,其余游客九折. (1)分别写出两旅行社所报旅游费用y与人数x的函数关系式. (2)若有11人参加旅游,则应选择哪个旅行社? (3)当人数为多少时可随意选择?
4.某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,如图表示该公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1与y2的函数解析式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案.
解:(1)设y1=k1x(k1≠0).
将点(30,600)代入,可得k1=20,
∴y1=20x.
设y2=k2x+b(k2≠0).
将点(0,300),(30,600)分别代入,得b=300和30k2+b=600,
解得k2=10,b=300.
∴y2=10x+300.
5.为了号召市民向贫困山区的孩子捐赠衣物,某校八年级(1)班的同学准备发放倡议书,倡议书的制作有两种方案可供选择:
方案-:由复印店代做,所需费用y1与倡议书张数x满足如图的函数关系;
方案二:租赁机器自己制作,所需费用y2(包括租赁机器的费用和制作倡议书的费用)与倡议书张数x满足如图的函数关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
八年级
2.5一元一次不等式与一次函数
复习巩固
一元一次方程与一次函数有什么关系?
A
1.一元一次方程2x+1=0的解是( )
A.x=-2
D.x=2
B.x=-
C.x=
2.直线y=-2x+1与x轴的交点坐标为( )
A. (0,1)
B.(0,-1)
C.( ,0)
D.(- ,0)
3.直线y=-2x+1与y轴的交点坐标为( )
A. (0,1)
B.(0,-1)
C.( ,0)
D. (- ,0)
C
C
6.如图,是一次函数y=kx+b(k≠0)的图象
方程kx+b=0的解是________;
x=6
4.-元一次不等式-2x+1>0的解集是( )
A.x>1
B.x>
C.x<1
D.x<
5.自变量x取何值时,函数y=-2x+1的值大于0? ( )
A.x>1
B.x>
C.x<1.
D.x<
D
D
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联数
一次函数y=2x-5研究的是横坐标与纵坐标的取值问题,即(x,y),有时会遇到横坐标x取哪些值时纵坐标y>0的问题;而当y>0时,有不等式2x-5>0.
不等式2x-5>0研究的是x取哪些值时,2x-5>0成立. 因为y=2x-5,所以x取哪些值时, 2x-5>0成立的问题就是x取哪些值时, y>0 成立的问题.
x
○
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
(2.5 , 0)
y
对于一次函数y=2x-5,我们建立直角系,画出函数图象.
(0 , -5)
求不等式2x-5>0的解集实质就是求x取何值时,2x-5>0,即就是一次函数中x取何值时,y>0.意思就是在函数图象上纵坐标y的值是正数时,函数图像上的点所对应的横坐标x的值是多少?
○
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联
解不等式2x-5>0的解集是x>2.5,把它表示在数轴上为x取何值时,2x-5>0:
x
○
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
(2.5 , 0)
y
(0 , -5)
在函数图象上我们不难看到纵坐标y的值是正数时即纵坐标y的值在y轴的 正半轴上,对应的函数图象在 x轴的上方,这部分函数图象对应的横坐标x的值是x >2.5的实数.
所以在函数图象上当x >2.5时,y>0 .即上当x >2.5时, 2x-5>0 .
○
一元一次不等式2x-5>0与一次函数y=2x-5之间的关联
函数y=2x- 5的图象如图2- - 6所示,观察图象回答下列问题:
( 1) x取何值时,2x- 5=0?
(2) x取哪些值时,2x-5>0?
(3) x取哪些值时,2x-5<0?
(4) x取哪些值时,2x-5> 1 ?
X=2.5
X>2.5
X<2.5
X>3
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
问题:作出函数y=2x-5的图象,观察图象回答下列问题:
(1)x取何值时,2x-5=0?
(2)x取哪些值时, 2x-5>0?
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
x取何值时, y=0
即(?,0)
x取哪些值时,y>0
即(?,y>0)
( , 0)
方法点睛:X轴上方的图象y值大于0 .
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
问题:
作出函数y=2x-5的图象,观察图象回答下列问题:
(3)x取哪些值时, 2x-5<0?
x取哪些值时, y<0
即(?,y <0)
在函数图象上我们不难看到纵坐标y的值是负数时,纵坐标y的值在y轴的负半轴上,对应的函数图象在x轴的下方,这部分函数图象对应的横坐标x的值是x<2.5 的实数.
意思就是在函数图象上纵坐标y的值是负数时,函数图像上的点所对应的横坐标x的值是多少?
问题:作出函数y=2x-5的图象,观察图象回答下列问题:
(4)x取哪些值时, 2x-5>3?
“关于x 的不等式的问题”转化为 “关于函数值的问题 ”
x
0
1
2
3
4
5
6
-1
-2
-2
-1
-3
-4
-5
-6
1
2
3
4
5
6
y
x取哪些值时, y>3
即(?,y>3)
意思就是在函数图象上纵坐标y的值大于3时,函数图像上的点所对应的横坐标x的值是多少?
过纵坐标为3的点作一条直线平行于x轴这条直线,与y=2x-5相交于点(4 , 3),在函数图象上我们不难看到纵坐标y的值大于3时,纵坐标y的值在y轴上大于3 以上的部分,对应的函数图象在直线y=3的上方,这部分函数图象对应的横坐标x的值是x >4的实数.
(4 , 3)
想一想:
如果y=-2x-5,
那么当x取何
值时,y>0?
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
0
1
2
3
4
x
-5
y
y=-2x-5
解:由图可知,当x<-2.5时,y>0
由上述讨论易知:
函数、(方程) 不等式
“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ;
反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”
因此,
我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与函数 、方程是紧密联系着
的一个整体 。
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集.
(1)3x+6>0
(3)–x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4)–x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
练习:利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
做一做:
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
x
-2
0
10
8
6
4
2
100
90
80
70
60
50
40
30
20
10
/s
y/m
y
y
y
y
哥
哥
弟
弟
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
9秒
前9秒
9秒后
弟
哥
随堂练习:
已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2,你是怎样做的?与同伴交流。
x<2
例2、解不等式5x+4<2x+10 .
解法1:原不等式化为3x -6<0,
画出直线y = 3x -6(如图)
所以不等式的解集为x<2 .
函数图象法:
解不等式法:
解法2:画出直线y1 = 5x +4
y2 = 2x +10
x
y
0
2
y2=2x+10
y1=5x+4
y1 <y2
5x+4<2x+10
3x -6<0,
y<0
所以不等式的解集为x<2 .
本节知识归纳
课外作业
3.某单位计划10月份组织员工到外地旅游,估计人数在6~15之间.甲、乙两旅行社的服务质量相同,且对外报价都是200元,该单位联系时,甲旅行社表示可给予每位游客八折;乙旅行社表示,可先免去一位游客的旅游费用,其余游客九折. (1)分别写出两旅行社所报旅游费用y与人数x的函数关系式. (2)若有11人参加旅游,则应选择哪个旅行社? (3)当人数为多少时可随意选择?
解:(1)由题意,得 甲:y=200x×80%=160x; 乙:y=200×(x-1)×90%=180x-180. (2)当x=11时, 甲:y=160×11=1 760(元); 乙:y=180×11-180=1 800(元). ∵1 760<1 800,∴甲旅行社所报旅游费用少些,应选甲旅行社.
(3)由题意,得160x=180x-180, 解得x=9. 所以当人数为9时,两家旅行社的费用相同,可随意选择.
3.某单位计划10月份组织员工到外地旅游,估计人数在6~15之间.甲、乙两旅行社的服务质量相同,且对外报价都是200元,该单位联系时,甲旅行社表示可给予每位游客八折;乙旅行社表示,可先免去一位游客的旅游费用,其余游客九折. (1)分别写出两旅行社所报旅游费用y与人数x的函数关系式. (2)若有11人参加旅游,则应选择哪个旅行社? (3)当人数为多少时可随意选择?
4.某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,如图表示该公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1与y2的函数解析式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案.
解:(1)设y1=k1x(k1≠0).
将点(30,600)代入,可得k1=20,
∴y1=20x.
设y2=k2x+b(k2≠0).
将点(0,300),(30,600)分别代入,得b=300和30k2+b=600,
解得k2=10,b=300.
∴y2=10x+300.
5.为了号召市民向贫困山区的孩子捐赠衣物,某校八年级(1)班的同学准备发放倡议书,倡议书的制作有两种方案可供选择:
方案-:由复印店代做,所需费用y1与倡议书张数x满足如图的函数关系;
方案二:租赁机器自己制作,所需费用y2(包括租赁机器的费用和制作倡议书的费用)与倡议书张数x满足如图的函数关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
