8.3.2 实际问题与二元一次方程组课件(共24张PPT)
文档属性
| 名称 | 8.3.2 实际问题与二元一次方程组课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:00:44 | ||
图片预览





文档简介
(共24张PPT)
人教版 七年级数学下
8.3实际问题与二元一次方程组
---第二课时
学习目标
1.学会运用二元一次方程组解决较复杂的实际问题;(重点、难点)
2.进一步经历和体验方程组解决实际问题的过程.
回顾旧知
上节课,我们学习了利用二元一次方程组解决简单的实际问题,你还记得解决问题的一般步骤吗?
审 清题意,找出等量关系;
设 未知数x和y;
列 出二元一次方程组;
解 方程组;
检 验;
答 题.
合作探究---解决较为复杂的实际问题
探究1:如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
公路10千米
合作探究---解决较为复杂的实际问题
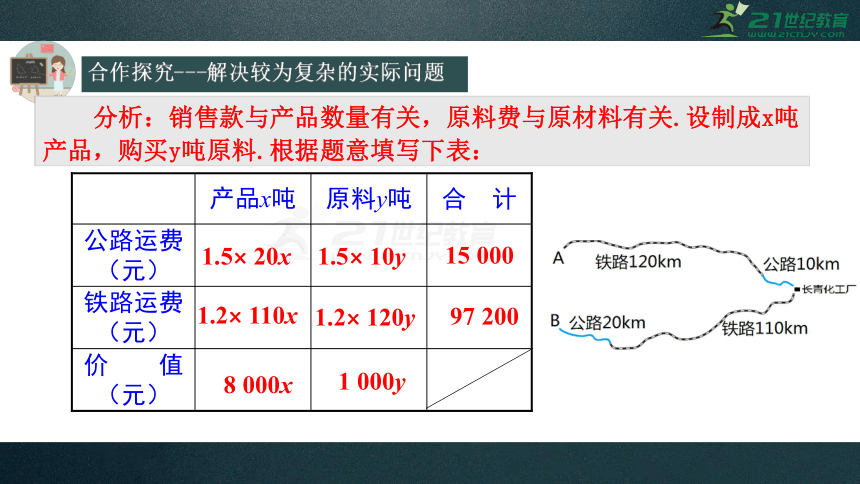
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
合作探究---解决较为复杂的实际问题
小试牛刀
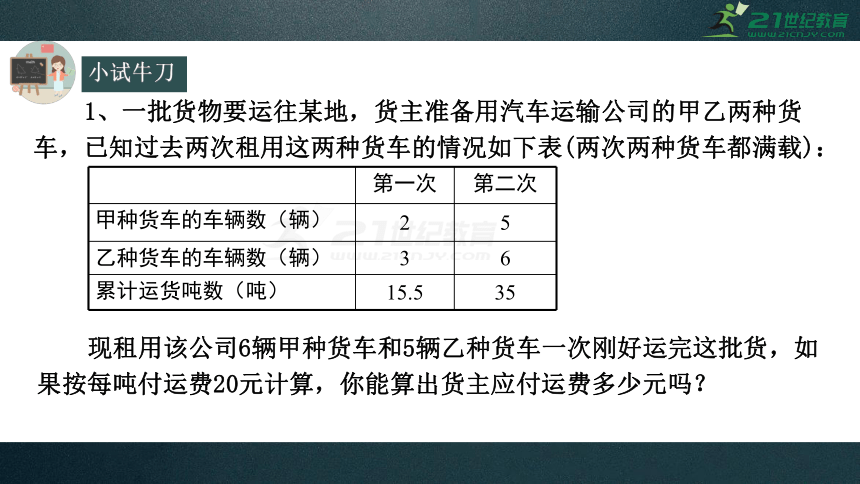
1、一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司6辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费20元计算,你能算出货主应付运费多少元吗?
小试牛刀
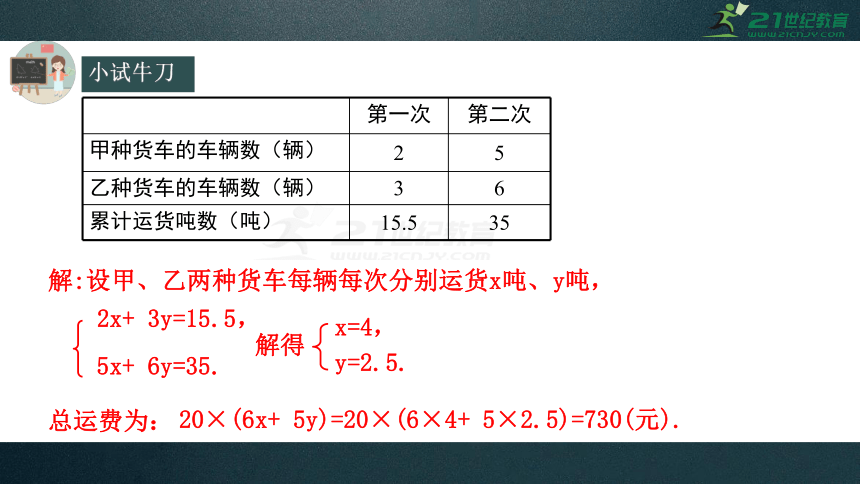
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
总运费为:
20×(6x+ 5y)=20×(6×4+ 5×2.5)=730(元).
合作探究---解决较为复杂的实际问题
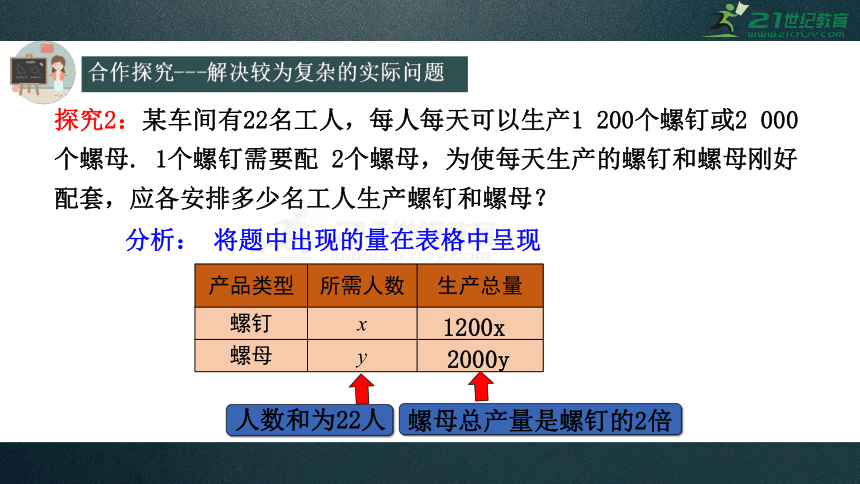
探究2:某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
合作探究---解决较为复杂的实际问题
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分
的比例;
(2)生产各部分的工人
数之和=工人总数.
小试牛刀
1、某工地挖掘机的台数和装卸机的台数之和为21,如果每台挖掘机每天平均挖土750m3,每台装卸机每天平均运土300m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机x台,装卸机y台,根据题意列出方程组得:
解得:
答:挖掘机有6台,装卸机有15台.
小试牛刀
2.一个工厂共42名工人,每个工人平均每小时生产圆形铁片120片或长方形铁片80片.已知两片圆形铁片与一片长方形铁片可以组成一个圆柱形密封的铁桶.你认为如何安排工人的生产,才能使每天生产的铁片正好配套?
解:设生产圆形铁片的工人x人,生产长方形铁片的工人y人,
根据题意列出方程组得:
解得:
答:生产圆形铁片的工人24人,生产长方形铁片的工人18人.
合作探究---解决较为复杂的实际问题
探究3:某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满。已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
合作探究---解决较为复杂的实际问题
解:(1)设这批游客的大数是x人,原计划租用y辆45座客车,
根据题意,得: 解得
答:这批游客的人数为240人,原计划租5辆45座客车
(2)租45座客车:240÷45≈5.3,:需租6辆租金为220×6=1320(元)。租60座客车:240÷60=4(辆),∴需租4辆,租金为300×4=1200(元)。∵1200<1320,∴租用4辆60座客车更合算
小试牛刀
1、一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
课后作业
解:设爸爸的设计方案中鸡场的宽为x米,长为y米,
根据题意得: 解得: ,y=15>14,不符合实际;
设妈妈的设计方案中鸡场的宽为a米,长为b米,
根据题意得: 解得: b=13<14,符合实际,
此时鸡场的面积为11×13=143(平方米)
答:妈妈的设计符合实际,鸡场的面积为143平方米。
课堂小结
1.在很多实际问题中,都存在着一些等量系,有的等量关系很明显,
有的则是隐含在题目中,需要我们去挖掘,在解决一些实际问题
时,我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具
体问题灵活选用.
畅谈收获:本节课你有哪些收获?
2.这种处理问题的过程可以进一步概括为(1)认真审题、分析问题
(2)找等量关系、列方程组 (3)解方程组、检验 (4)作答。
综合演练
1.某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
解:设需含蛋白质为20%、12%的配料分别为xkg、ykg, 根据题意列出方程组得
解得
答:需含蛋白质为20%、12%的配料分别为37.5kg、62.5kg
综合演练
2、某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,改种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排种植才能使所有人都参与种植,且资金正好够用?
综合演练
解:设蔬菜种植x 公顷,荞麦种植y 公顷
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 公顷
人员安排为为: 5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都参与种植且资金正好够用.
综合演练
3、某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元。当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工每天可加工6吨,但两种加工方式不能同时进行受季节条件的限制,公司必须在15天之内将这批蔬菜处理完毕,为此公司研制了三种加工方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及加工的蔬菜在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天完成你认为选择哪种方案获利最多?为什么?
综合演练
解:方案一:获利为4500×140=630000(元).
方案二:获利为
7500×6×151000×(140-6×15)=675000+50000=725000(元).
方案三:设将x吨蔬菜进行精加工,y吨蔬菜进行粗加工;
根据题意得: ,解得:
所以方案三获利为:7500×60+4500×80=810000(元)
因为630000<725000<810000,所以选择方案三获利最多。
课后作业
课本教材第102页:4、7、8题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
8.3实际问题与二元一次方程组
---第二课时
学习目标
1.学会运用二元一次方程组解决较复杂的实际问题;(重点、难点)
2.进一步经历和体验方程组解决实际问题的过程.
回顾旧知
上节课,我们学习了利用二元一次方程组解决简单的实际问题,你还记得解决问题的一般步骤吗?
审 清题意,找出等量关系;
设 未知数x和y;
列 出二元一次方程组;
解 方程组;
检 验;
答 题.
合作探究---解决较为复杂的实际问题
探究1:如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
公路10千米
合作探究---解决较为复杂的实际问题
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
合作探究---解决较为复杂的实际问题
小试牛刀
1、一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司6辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费20元计算,你能算出货主应付运费多少元吗?
小试牛刀
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
总运费为:
20×(6x+ 5y)=20×(6×4+ 5×2.5)=730(元).
合作探究---解决较为复杂的实际问题
探究2:某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
合作探究---解决较为复杂的实际问题
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分
的比例;
(2)生产各部分的工人
数之和=工人总数.
小试牛刀
1、某工地挖掘机的台数和装卸机的台数之和为21,如果每台挖掘机每天平均挖土750m3,每台装卸机每天平均运土300m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机x台,装卸机y台,根据题意列出方程组得:
解得:
答:挖掘机有6台,装卸机有15台.
小试牛刀
2.一个工厂共42名工人,每个工人平均每小时生产圆形铁片120片或长方形铁片80片.已知两片圆形铁片与一片长方形铁片可以组成一个圆柱形密封的铁桶.你认为如何安排工人的生产,才能使每天生产的铁片正好配套?
解:设生产圆形铁片的工人x人,生产长方形铁片的工人y人,
根据题意列出方程组得:
解得:
答:生产圆形铁片的工人24人,生产长方形铁片的工人18人.
合作探究---解决较为复杂的实际问题
探究3:某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满。已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
合作探究---解决较为复杂的实际问题
解:(1)设这批游客的大数是x人,原计划租用y辆45座客车,
根据题意,得: 解得
答:这批游客的人数为240人,原计划租5辆45座客车
(2)租45座客车:240÷45≈5.3,:需租6辆租金为220×6=1320(元)。租60座客车:240÷60=4(辆),∴需租4辆,租金为300×4=1200(元)。∵1200<1320,∴租用4辆60座客车更合算
小试牛刀
1、一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
课后作业
解:设爸爸的设计方案中鸡场的宽为x米,长为y米,
根据题意得: 解得: ,y=15>14,不符合实际;
设妈妈的设计方案中鸡场的宽为a米,长为b米,
根据题意得: 解得: b=13<14,符合实际,
此时鸡场的面积为11×13=143(平方米)
答:妈妈的设计符合实际,鸡场的面积为143平方米。
课堂小结
1.在很多实际问题中,都存在着一些等量系,有的等量关系很明显,
有的则是隐含在题目中,需要我们去挖掘,在解决一些实际问题
时,我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具
体问题灵活选用.
畅谈收获:本节课你有哪些收获?
2.这种处理问题的过程可以进一步概括为(1)认真审题、分析问题
(2)找等量关系、列方程组 (3)解方程组、检验 (4)作答。
综合演练
1.某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
解:设需含蛋白质为20%、12%的配料分别为xkg、ykg, 根据题意列出方程组得
解得
答:需含蛋白质为20%、12%的配料分别为37.5kg、62.5kg
综合演练
2、某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,改种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排种植才能使所有人都参与种植,且资金正好够用?
综合演练
解:设蔬菜种植x 公顷,荞麦种植y 公顷
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 公顷
人员安排为为: 5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都参与种植且资金正好够用.
综合演练
3、某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元。当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工每天可加工6吨,但两种加工方式不能同时进行受季节条件的限制,公司必须在15天之内将这批蔬菜处理完毕,为此公司研制了三种加工方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及加工的蔬菜在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天完成你认为选择哪种方案获利最多?为什么?
综合演练
解:方案一:获利为4500×140=630000(元).
方案二:获利为
7500×6×151000×(140-6×15)=675000+50000=725000(元).
方案三:设将x吨蔬菜进行精加工,y吨蔬菜进行粗加工;
根据题意得: ,解得:
所以方案三获利为:7500×60+4500×80=810000(元)
因为630000<725000<810000,所以选择方案三获利最多。
课后作业
课本教材第102页:4、7、8题
https://www.21cnjy.com/help/help_extract.php
