人教版九年级下册数学 第二十八章锐角三角函数复习课件(共20张PPT)
文档属性
| 名称 | 人教版九年级下册数学 第二十八章锐角三角函数复习课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 527.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 16:14:49 | ||
图片预览




文档简介
(共20张PPT)
本章知识结构梳理
2、30°、45°、60°特殊角的三角函数值。
⑶、解直角三角形在实际问题中
的应用。
知识回顾1
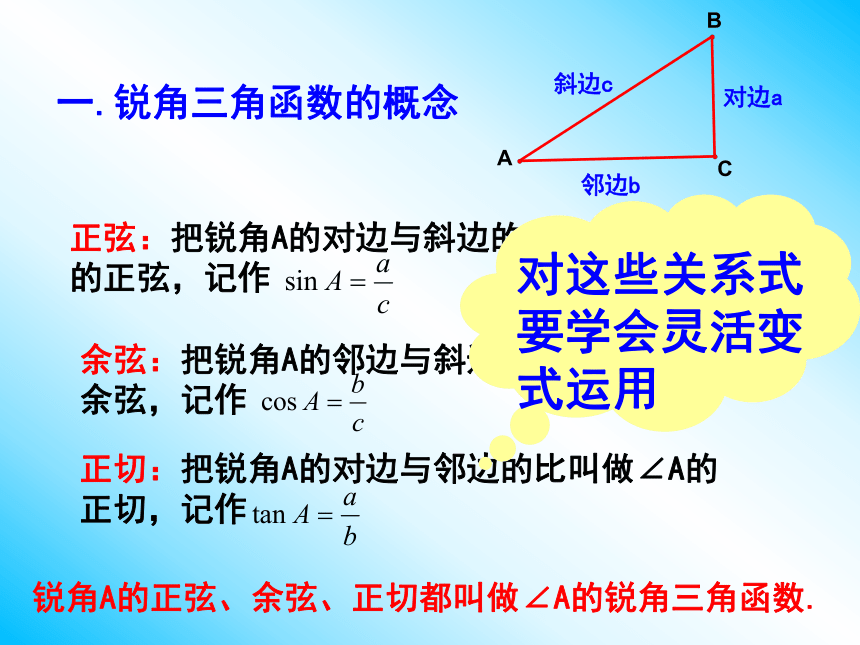
一.锐角三角函数的概念
正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
对边a
邻边b
斜边c
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
同一锐角的正弦值和余弦值之间的关系是:正弦值等于它的余角的余弦值,余弦值等于它的余角的正弦值.
即sinA=cos(90°一 A)=cosB cosA=sin(90°一A)=sinB
思考:同一个锐角的正弦值和余弦值之间有何关系?
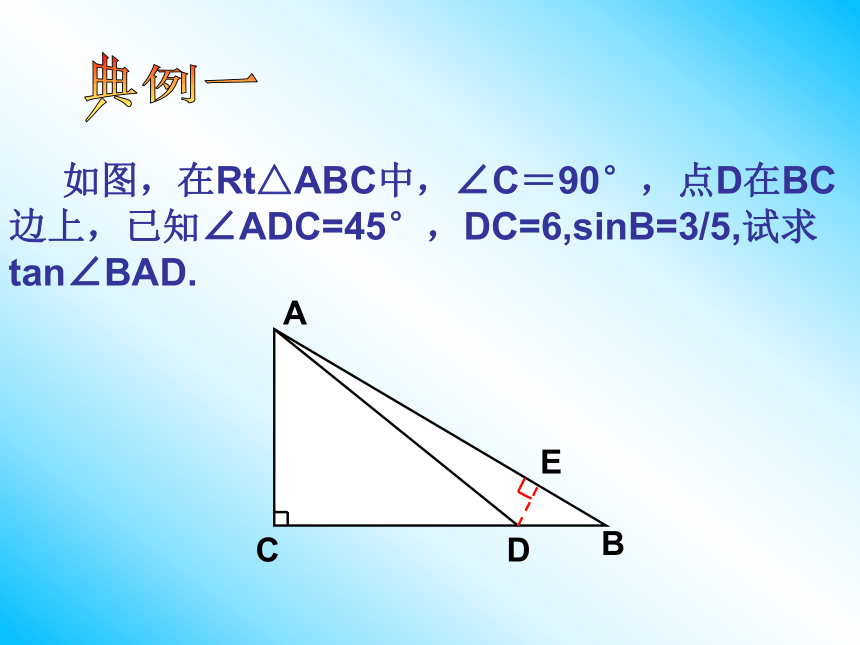
如图,在Rt△ABC中,∠C=90°,点D在BC边上,已知∠ADC=45°,DC=6,sinB=3/5,试求tan∠BAD.
A
C
B
D
知识回顾2
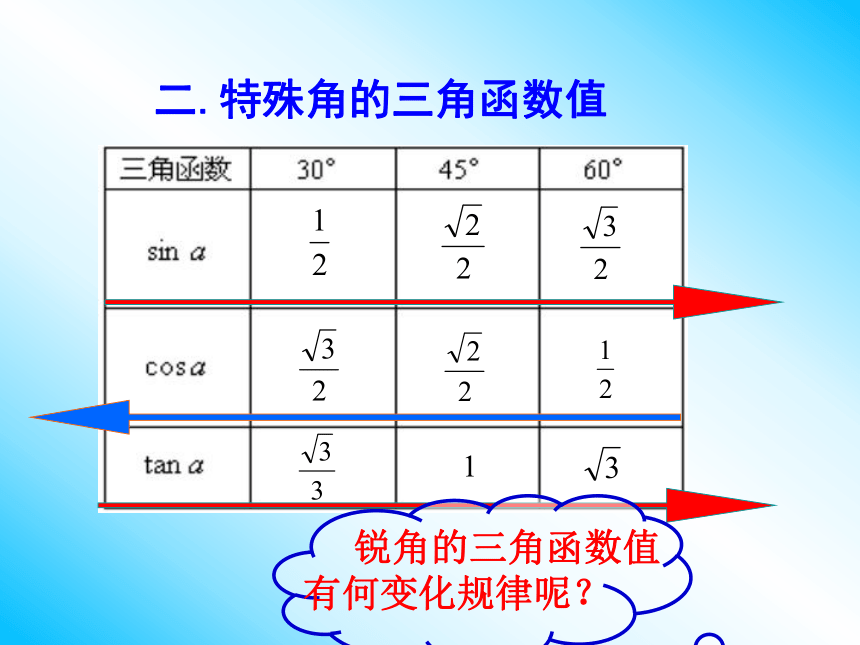
二.特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
1.计算2sin30 °+tan45 ° ×cos60°
步骤:
一“代”二“算”
30°
知识回顾3
三.解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是边),就可以求出其余3个未知元素.
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,求b、c的大小.
解:
∵ sinA=a/c,
∴ c=a/sinA=5/sin30=5/(1/2)=10.
解直角三角形分为两类:一是已知一边一角解直角三角形;二是已知两边解直角三角形.
知识回顾4
四.解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
铅直线
水平线
视线
视线
仰角
俯角
2.方向角
指南或北的方向线与目标方向线构成小于90°的角,叫做方向角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则
3.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
h
l
海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
45°
80°
D
4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC.
(1)AC与BD相等吗?说明理由;
4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC.
(1)AC与BD相等吗?说明理由;
2.30°、45°、60°特殊角的三角函数值
⑶解直角三角形在实际问题中
的应用
本章知识结构梳理
2、30°、45°、60°特殊角的三角函数值。
⑶、解直角三角形在实际问题中
的应用。
知识回顾1
一.锐角三角函数的概念
正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
对边a
邻边b
斜边c
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
同一锐角的正弦值和余弦值之间的关系是:正弦值等于它的余角的余弦值,余弦值等于它的余角的正弦值.
即sinA=cos(90°一 A)=cosB cosA=sin(90°一A)=sinB
思考:同一个锐角的正弦值和余弦值之间有何关系?
如图,在Rt△ABC中,∠C=90°,点D在BC边上,已知∠ADC=45°,DC=6,sinB=3/5,试求tan∠BAD.
A
C
B
D
知识回顾2
二.特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
1.计算2sin30 °+tan45 ° ×cos60°
步骤:
一“代”二“算”
30°
知识回顾3
三.解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是边),就可以求出其余3个未知元素.
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,求b、c的大小.
解:
∵ sinA=a/c,
∴ c=a/sinA=5/sin30=5/(1/2)=10.
解直角三角形分为两类:一是已知一边一角解直角三角形;二是已知两边解直角三角形.
知识回顾4
四.解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
铅直线
水平线
视线
视线
仰角
俯角
2.方向角
指南或北的方向线与目标方向线构成小于90°的角,叫做方向角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则
3.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
h
l
海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
45°
80°
D
4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC.
(1)AC与BD相等吗?说明理由;
4.如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC.
(1)AC与BD相等吗?说明理由;
2.30°、45°、60°特殊角的三角函数值
⑶解直角三角形在实际问题中
的应用
