2020春北师大版七下数学第四章三角形复习探究式教学课件(24张ppt)
文档属性
| 名称 | 2020春北师大版七下数学第四章三角形复习探究式教学课件(24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览







文档简介
课件24张PPT。北京师范大学出版社 七年级 | 下册 课前小测课堂精讲课后作业北京师范大学出版社 七年级 | 下册 课前小测北京师范大学出版社 七年级 | 下册 知识小测
1.三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
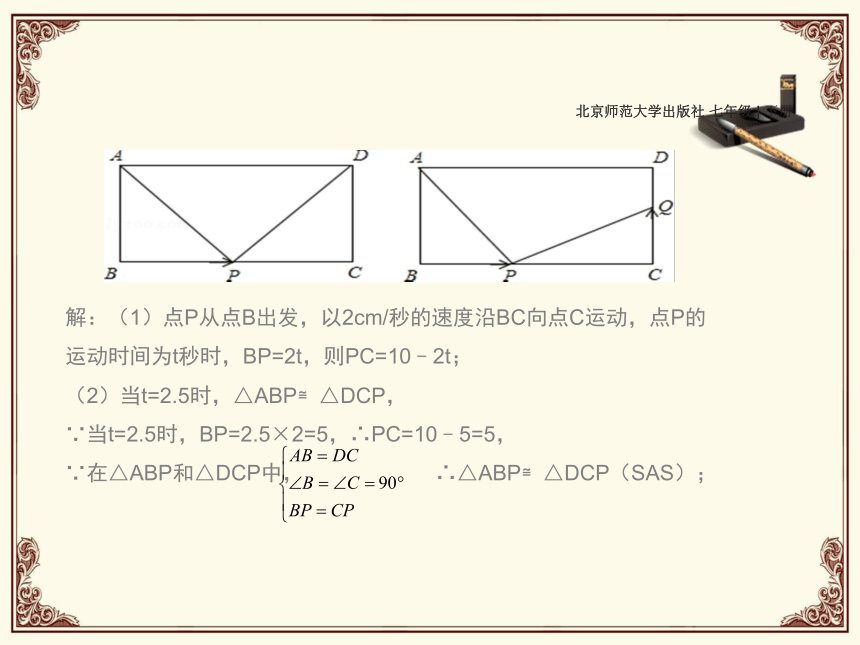
A.5 B.6 C.11 D.16CC北京师范大学出版社 七年级 | 下册 2.小华问小明:“如图所示的三角形,已知最长边为9,最短边为4,如何求这个三角形的面积?小明提示说:“可通过作已知一边上的高的方法来解决.”根据小明的提示,小华作出的正确图形是( )(2)当t=2.5时,△ABP≌△DCP,
∵当t=2.5时,BP=2.5×2=5,∴PC=10﹣5=5,
∵在△ABP和△DCP中, ∴△ABP≌△DCP(SAS);解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,则PC=10﹣2t;北京师范大学出版社 七年级 | 下册 ?北京师范大学出版社 七年级 | 下册 类比精练2.
如图,已知△ABC中,
AB=AC=10cm,BC=8cm,点
D为AB的中点.如果点P在线段
BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
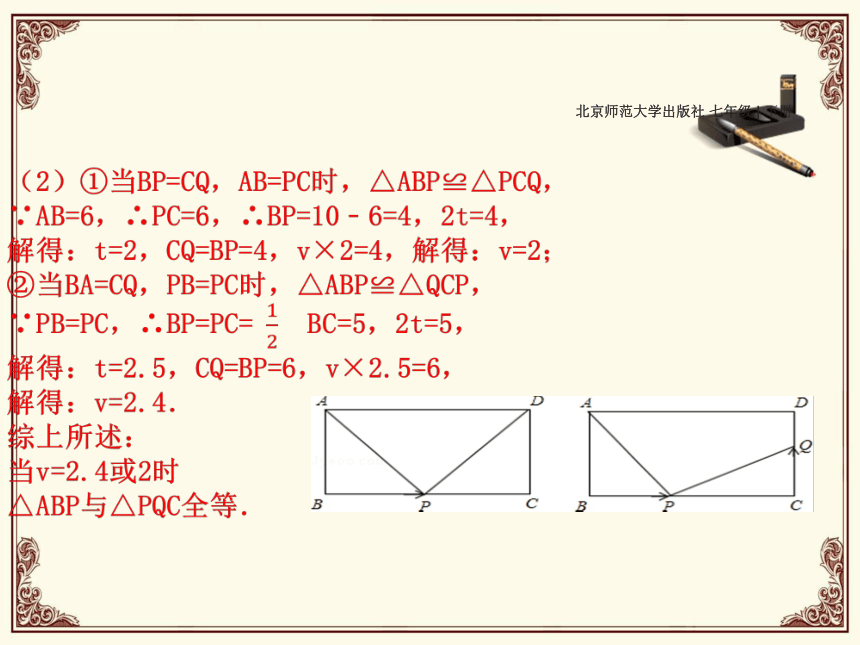
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?北京师范大学出版社 七年级 | 下册 ?北京师范大学出版社 七年级 | 下册 (2)∵vP≠vQ,∴BP≠CQ,
又∵△BPD≌△CQP,∠B=∠C,
则BP=PC=4,CQ=BD=5,
∴点P,点Q运动的时间 (s),
∴vQ= (cm/s),
答:当点Q的运动速度为 cm/s,能够使△BPD与△CQP全等.北京师范大学出版社 七年级 | 下册 课后作业北京师范大学出版社 七年级 | 下册 3.三角形三条高的交点一定在( )
A.三角形内部 B.三角形外部
C.三角形内部或外部
D.三角形内部、外部或顶点
4.若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形DA北京师范大学出版社 七年级 | 下册 5.如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
6.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D.SSS
AA北京师范大学出版社 七年级 | 下册 7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
A.1 B.1或3
C.1或7 D.3或7C北京师范大学出版社 七年级 | 下册 8.在Rt△ABC中,∠C=90°,∠A=65°,则∠B= .
9.边长为整数并且最大边长是5的三角形共有 个.
10.如图,BD与CE分别是∠ABC和∠ACB的平分线,
如果∠DBC=∠ECB,那么∠ABC=∠ACB吗? .25° 9相等北京师范大学出版社 七年级 | 下册 11.如图,已知AC=DB,要使△ABC≌△DCB,
只需增加的一个条件是 _或
.
12.已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.
∠ABC=∠DCBAC=DB解:根据三角形的三边关系可得:
8﹣3<BC<8+3,
即:5<BC<11,
∵BC为奇数,∴BC的长为7或9.北京师范大学出版社 七年级 | 下册 13.已知△ABC的三边长均为整数,△ABC的周长为奇数.
(1)若AC=8,BC=2,求AB的长;
(2)若AC﹣BC=5,求AB的最小值.解:(1)∵由三角形的三边关系知,AC﹣BC<AB<AC+BC,
即:8﹣2<AB<8+2,
∴6<AB<10,
又∵△ABC的周长为奇数,而AC、BC为偶数,
∴AB为奇数,故AB=7或9;北京师范大学出版社 七年级 | 下册 (2)∵AC﹣BC=5,
∴AC、BC中一个奇数、一个偶数,
又∵△ABC的周长为奇数,故AB为偶数,
∴AB>AC﹣BC=5,得AB的最小值为6.北京师范大学出版社 七年级 | 下册 14.如图,△ABC中,AD是高,AE、BF
是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,
求∠DAE和∠BOA的度数.解:∵∠A=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.故∠DAE=5°,∠BOA=120°.北京师范大学出版社 七年级 | 下册 15.尺规作图:已知线段a,求作三角形ABC,使AB=BC=CA=a.(要求保留作图痕迹)解:如图,△ABC为所作.北京师范大学出版社 七年级 | 下册 16.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).
(1)你添加的条件是 .
(2)添加条件后,请说明△ABC≌△ADE的理由.∠C=∠E(2)选∠C=∠E为条件.
理由如下:
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS).北京师范大学出版社 七年级 | 下册 17.已知:如图,
点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).北京师范大学出版社 七年级 | 下册 18.有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?解:在△ABC和△CED中,
AC=CD,∠ACB=∠ECD(对顶角),EC=BC,
∴△ABC≌△DEC,
∴AB=ED,
即量出DE的长,就是A、B的距离北京师范大学出版社 七年级 | 下册 19.如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
A.180° B.225°
C.270° D.315°B北京师范大学出版社 七年级 | 下册 20.已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB.证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).北京师范大学出版社 七年级 | 下册
1.三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16CC北京师范大学出版社 七年级 | 下册 2.小华问小明:“如图所示的三角形,已知最长边为9,最短边为4,如何求这个三角形的面积?小明提示说:“可通过作已知一边上的高的方法来解决.”根据小明的提示,小华作出的正确图形是( )(2)当t=2.5时,△ABP≌△DCP,
∵当t=2.5时,BP=2.5×2=5,∴PC=10﹣5=5,
∵在△ABP和△DCP中, ∴△ABP≌△DCP(SAS);解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,则PC=10﹣2t;北京师范大学出版社 七年级 | 下册 ?北京师范大学出版社 七年级 | 下册 类比精练2.
如图,已知△ABC中,
AB=AC=10cm,BC=8cm,点
D为AB的中点.如果点P在线段
BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?北京师范大学出版社 七年级 | 下册 ?北京师范大学出版社 七年级 | 下册 (2)∵vP≠vQ,∴BP≠CQ,
又∵△BPD≌△CQP,∠B=∠C,
则BP=PC=4,CQ=BD=5,
∴点P,点Q运动的时间 (s),
∴vQ= (cm/s),
答:当点Q的运动速度为 cm/s,能够使△BPD与△CQP全等.北京师范大学出版社 七年级 | 下册 课后作业北京师范大学出版社 七年级 | 下册 3.三角形三条高的交点一定在( )
A.三角形内部 B.三角形外部
C.三角形内部或外部
D.三角形内部、外部或顶点
4.若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形DA北京师范大学出版社 七年级 | 下册 5.如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
6.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D.SSS
AA北京师范大学出版社 七年级 | 下册 7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
A.1 B.1或3
C.1或7 D.3或7C北京师范大学出版社 七年级 | 下册 8.在Rt△ABC中,∠C=90°,∠A=65°,则∠B= .
9.边长为整数并且最大边长是5的三角形共有 个.
10.如图,BD与CE分别是∠ABC和∠ACB的平分线,
如果∠DBC=∠ECB,那么∠ABC=∠ACB吗? .25° 9相等北京师范大学出版社 七年级 | 下册 11.如图,已知AC=DB,要使△ABC≌△DCB,
只需增加的一个条件是 _或
.
12.已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.
∠ABC=∠DCBAC=DB解:根据三角形的三边关系可得:
8﹣3<BC<8+3,
即:5<BC<11,
∵BC为奇数,∴BC的长为7或9.北京师范大学出版社 七年级 | 下册 13.已知△ABC的三边长均为整数,△ABC的周长为奇数.
(1)若AC=8,BC=2,求AB的长;
(2)若AC﹣BC=5,求AB的最小值.解:(1)∵由三角形的三边关系知,AC﹣BC<AB<AC+BC,
即:8﹣2<AB<8+2,
∴6<AB<10,
又∵△ABC的周长为奇数,而AC、BC为偶数,
∴AB为奇数,故AB=7或9;北京师范大学出版社 七年级 | 下册 (2)∵AC﹣BC=5,
∴AC、BC中一个奇数、一个偶数,
又∵△ABC的周长为奇数,故AB为偶数,
∴AB>AC﹣BC=5,得AB的最小值为6.北京师范大学出版社 七年级 | 下册 14.如图,△ABC中,AD是高,AE、BF
是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,
求∠DAE和∠BOA的度数.解:∵∠A=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.故∠DAE=5°,∠BOA=120°.北京师范大学出版社 七年级 | 下册 15.尺规作图:已知线段a,求作三角形ABC,使AB=BC=CA=a.(要求保留作图痕迹)解:如图,△ABC为所作.北京师范大学出版社 七年级 | 下册 16.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).
(1)你添加的条件是 .
(2)添加条件后,请说明△ABC≌△ADE的理由.∠C=∠E(2)选∠C=∠E为条件.
理由如下:
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS).北京师范大学出版社 七年级 | 下册 17.已知:如图,
点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).北京师范大学出版社 七年级 | 下册 18.有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?解:在△ABC和△CED中,
AC=CD,∠ACB=∠ECD(对顶角),EC=BC,
∴△ABC≌△DEC,
∴AB=ED,
即量出DE的长,就是A、B的距离北京师范大学出版社 七年级 | 下册 19.如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
A.180° B.225°
C.270° D.315°B北京师范大学出版社 七年级 | 下册 20.已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB.证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).北京师范大学出版社 七年级 | 下册
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
