4.3.2 空间两点间的距离公式 课件 26张PPT
文档属性
| 名称 | 4.3.2 空间两点间的距离公式 课件 26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
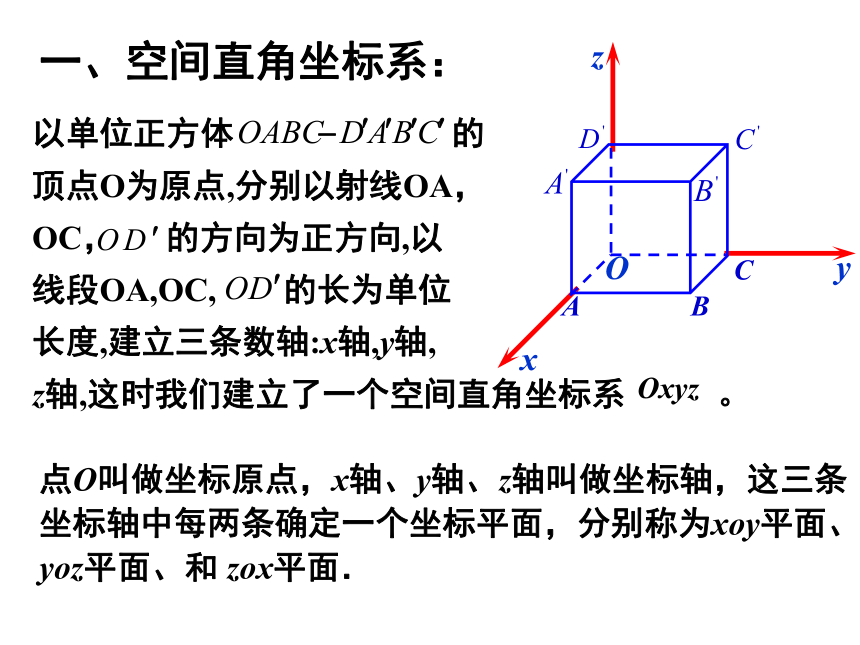
一、空间直角坐标系:
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.
右手直角坐标系
空间直角坐标系共有八个卦限
2、空间直角坐标系的划分:
o
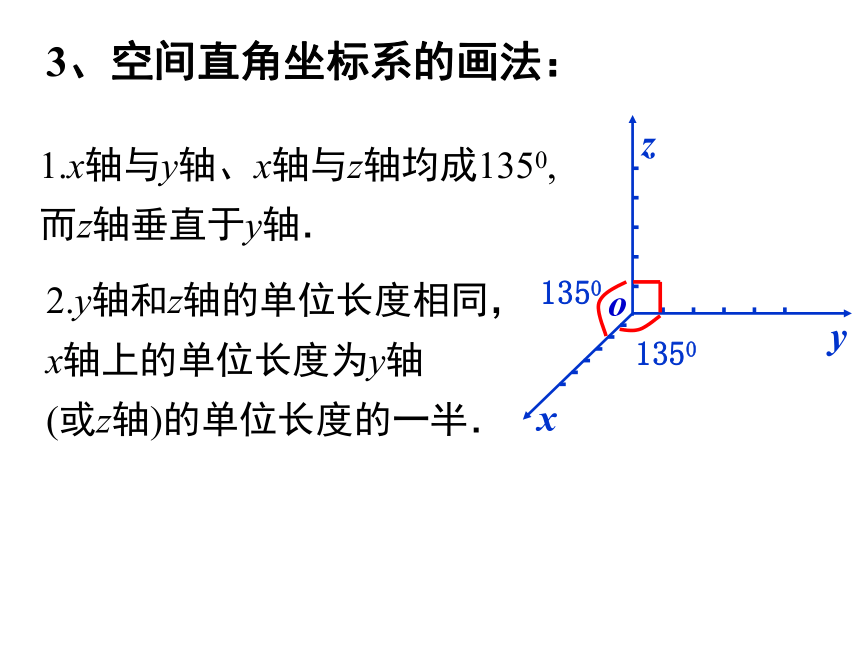
1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.
2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
(或z轴)的单位长度的一半.
3、空间直角坐标系的画法:
空间直角坐标系中任意一点的位置如何表示?
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
二、空间点的坐标
M’
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
M’
O
P
M’
Q
O
M
R
这样空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.
?
?
M0
x
y
z
方法二:过M点作xOy面的垂线,垂足为M0点。点M0在坐标系xOy中的坐标x、y依次是M点的横坐标、纵坐标。再过M点作z轴的垂线,垂足M1在z轴上的坐标z就是M点的竖坐标。
M点坐标为(x,y,z)
M1
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
三、特殊位置的点的坐标:
?
A1(1,4,0)
?
A(1,4,1)
?
(2,-2,0)
B1
?
B
(2,-2,-1)
?
(-1,-3,0)
C1
?
(-1,-3,3)
C
练习1
在空间直角坐标系中作出下列各点 A(1,4,1) B(2,-2,-1) C(1,-3,3)
如下图,在长方体OABC-D'A'B'C',|OA|=3,|OC|=4,|OD'|=3,A'C'与B'D'相交于点P.分别写出点C,B',P的坐标.
O
B
A'
B'
C'
P
P'
3
4
3
练习2
两点间距离公式
类比
猜想
四、空间两点间的距离公式
引申:
推导:
空间两点的距离公式
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),求:
(1)三角形三边的边长;
解:
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),求:
(2)BC边上中线AM的长。
解:
练1.求空间两点
间的距离
练2.平面上到坐标原点的距离为1的点的轨 迹是单位圆,其方程为 在空间中,到坐标原点的距离为1的点的轨迹是什么?试写出它的方程。
练3.已知三点
、
证明:
三点在同一直线上.
练4、证明以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形△ABC是一等腰三角形.
五、练习提升
A
A1
B
B1
C
C1
y
x
A
A1
B
B1
C
C1
y
x
1、空间直角坐标系的建立及特点
2、空间两点间的距离公式
六、课堂小结
一、空间直角坐标系:
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.
右手直角坐标系
空间直角坐标系共有八个卦限
2、空间直角坐标系的划分:
o
1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.
2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
(或z轴)的单位长度的一半.
3、空间直角坐标系的画法:
空间直角坐标系中任意一点的位置如何表示?
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
二、空间点的坐标
M’
O
设点P、Q和R在x 轴、y 轴和z 轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).
反过来,给定有序实数组(x,y,z),我们可以在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
M’
O
P
M’
Q
O
M
R
这样空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.
?
?
M0
x
y
z
方法二:过M点作xOy面的垂线,垂足为M0点。点M0在坐标系xOy中的坐标x、y依次是M点的横坐标、纵坐标。再过M点作z轴的垂线,垂足M1在z轴上的坐标z就是M点的竖坐标。
M点坐标为(x,y,z)
M1
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
三、特殊位置的点的坐标:
?
A1(1,4,0)
?
A(1,4,1)
?
(2,-2,0)
B1
?
B
(2,-2,-1)
?
(-1,-3,0)
C1
?
(-1,-3,3)
C
练习1
在空间直角坐标系中作出下列各点 A(1,4,1) B(2,-2,-1) C(1,-3,3)
如下图,在长方体OABC-D'A'B'C',|OA|=3,|OC|=4,|OD'|=3,A'C'与B'D'相交于点P.分别写出点C,B',P的坐标.
O
B
A'
B'
C'
P
P'
3
4
3
练习2
两点间距离公式
类比
猜想
四、空间两点间的距离公式
引申:
推导:
空间两点的距离公式
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),求:
(1)三角形三边的边长;
解:
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),求:
(2)BC边上中线AM的长。
解:
练1.求空间两点
间的距离
练2.平面上到坐标原点的距离为1的点的轨 迹是单位圆,其方程为 在空间中,到坐标原点的距离为1的点的轨迹是什么?试写出它的方程。
练3.已知三点
、
证明:
三点在同一直线上.
练4、证明以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形△ABC是一等腰三角形.
五、练习提升
A
A1
B
B1
C
C1
y
x
A
A1
B
B1
C
C1
y
x
1、空间直角坐标系的建立及特点
2、空间两点间的距离公式
六、课堂小结
