4.3.2 空间两点间的距离公式 课件 27张PPT
文档属性
| 名称 | 4.3.2 空间两点间的距离公式 课件 27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 10:26:22 | ||
图片预览


文档简介
(共27张PPT)
4.3 空间直角坐标系
人教A版 必修2 第四章
x
O
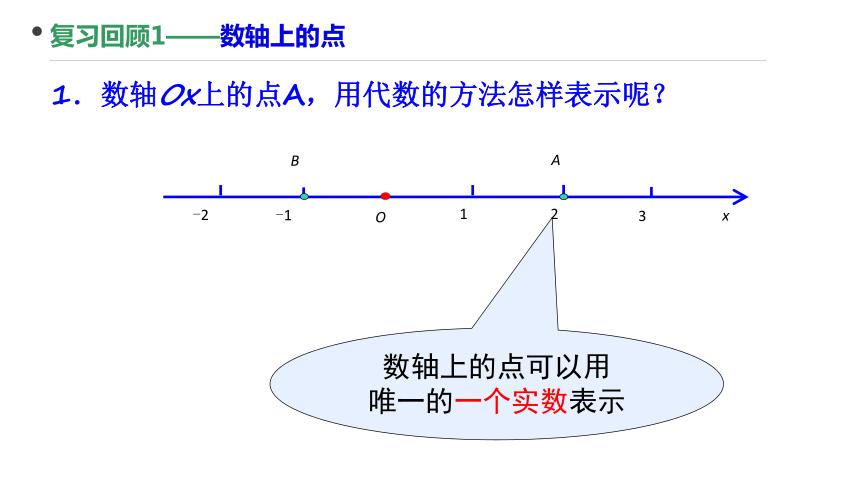
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
复习回顾1——数轴上的点
1.数轴Ox上的点A,用代数的方法怎样表示呢?
x
y
A
O
x
y
(x,y)
平面中的点可以用有序实数对(x,y)来表示点
复习回顾2——平面直角坐标系中的点
2.直角坐标平面上的点A,怎样表示呢?
平面直角坐标系
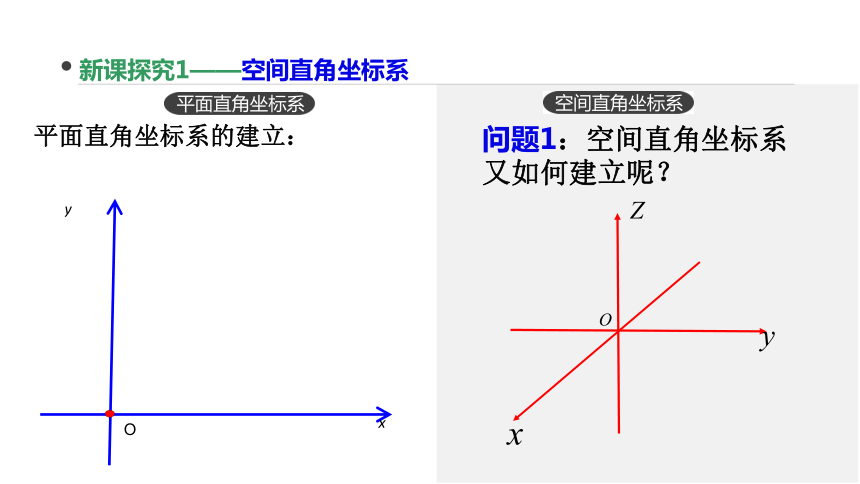
新课探究1——空间直角坐标系
平面直角坐标系的建立:
问题1:空间直角坐标系又如何建立呢?
x
y
O
空间直角坐标系
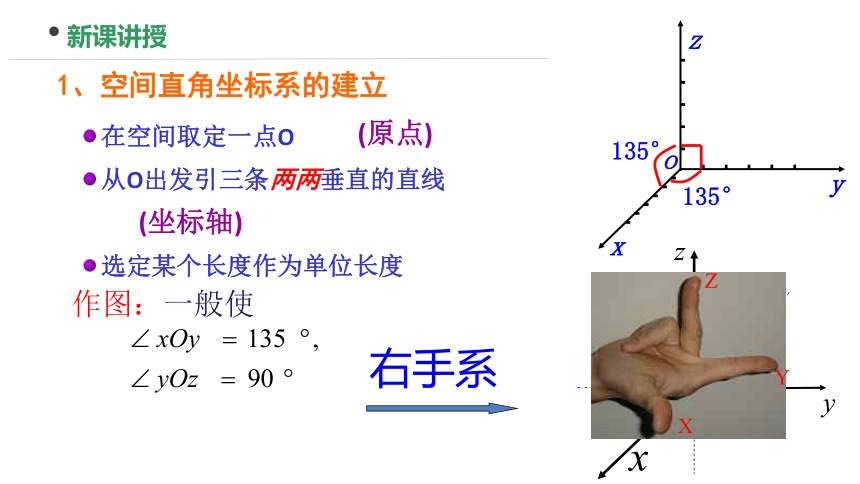
1、空间直角坐标系的建立
在空间取定一点O
从O出发引三条两两垂直的直线
选定某个长度作为单位长度
(原点)
(坐标轴)
右手系
作图:一般使
新课讲授
o
x
y
z
135°
135°
X
Y
Z
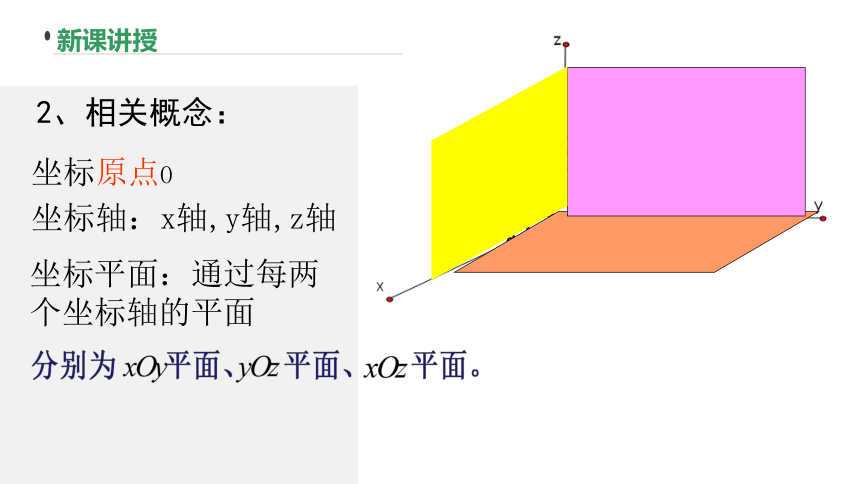
坐标平面:通过每两个坐标轴的平面
坐标原点O
坐标轴:x轴,y轴,z轴
2、相关概念:
新课讲授
平面直角坐标系
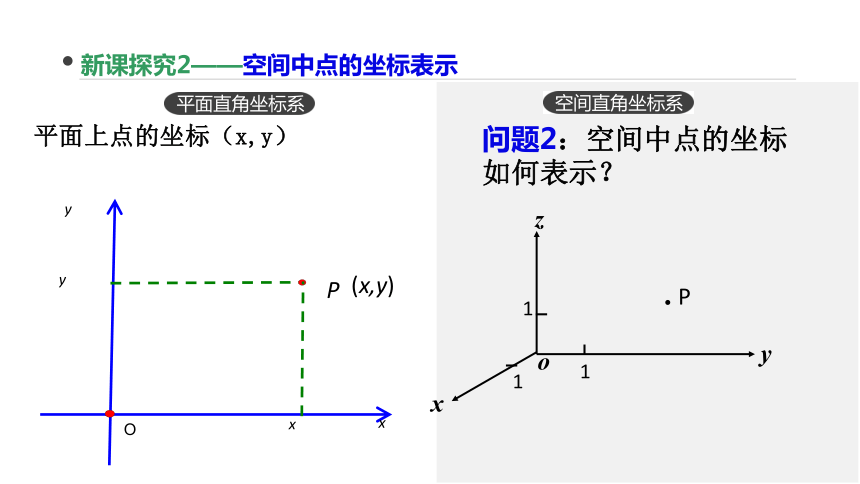
新课探究2——空间中点的坐标表示
平面上点的坐标(x,y)
问题2:空间中点的坐标如何表示?
x
y
P
x
y
(x,y)
O
1
1
1
?
P
空间直角坐标系
?
1
1
1
?
P
?
P0
x
y
z
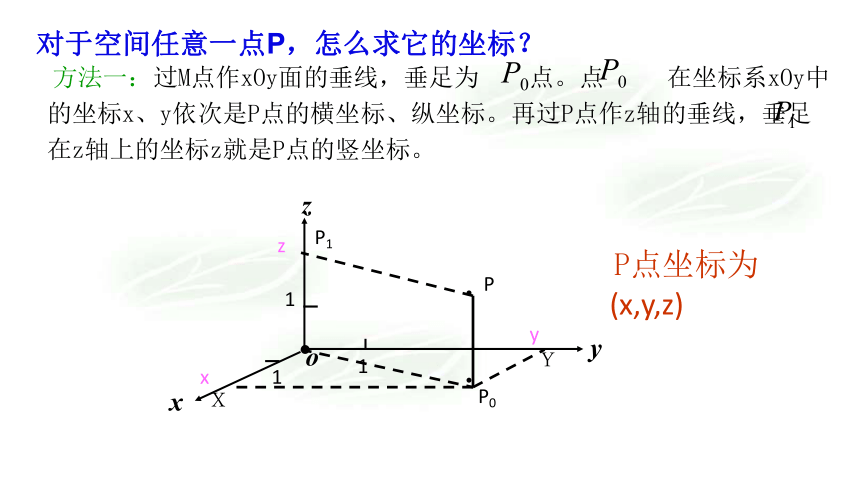
P点坐标为
(x,y,z)
P1
方法一:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。
X
Y
对于空间任意一点P,怎么求它的坐标?
P
Q
R
y
x
z
1
1
P
?
1
?
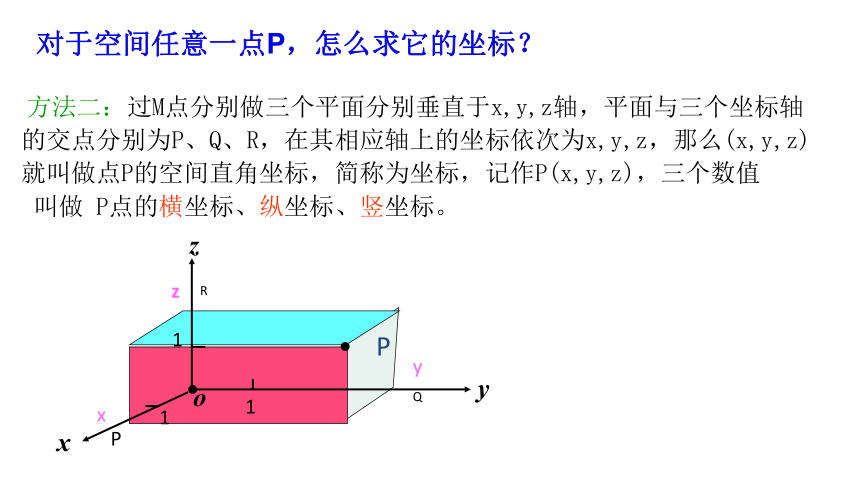
对于空间任意一点P,怎么求它的坐标?
方法二:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。
P
O
y
x
z
C
D
练习1:写出点P的坐标
(1)DP=2,CP=4
P(2,4,0)
知识运用
P
O
y
x
z
P1
C
D
P(2,4,5)
练习1:写出点P的坐标
(2)DP1=2,CP1=4,P1P=5
知识运用
P
O
y
x
z
P1
P(2,4,-5)
知识运用
练习1:写出点P的坐标
(3)DP1=2,CP1=4,P1P=-5
C
D
y
x
?
O
z
1
1
1
?
?
?
A
B
C
?
D
E
F
?
?
练习2:在空间直角坐标系中描出下列各点,并说明这些点的位置 A(0,1,1),B(0,0,2),C(0,2,0),
D(1,0,3),E(2,2,0),F(1,0,0)
知识运用
知识运用
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
二、坐标平面内的点
一、坐标轴上的点
规律总结:
O
x
y
z
P(x,y,z)
1.点P(x , y , z) 在下列坐标平面中的射影点为:
(1)在xoy平面射影点为P1__________;
(2)在xoz平面射影点为P2__________;
(3)在yoz平面射影点为P3__________;
P1
P2
(x,y,0)
(x,0,z)
P3
(0,y,z)
变式练习——空间中点的射影点与对称点坐标
2.点P(x , y , z) 关于坐标平面的对称点:
(1)关于xoy平面对称的点P1为__________;
(2)关于yoz平面对称的点P2为__________;
(3)关于xoz平面对称的点P3为__________;
关于谁对称谁不变
(x,y,-z)
(-x,y,z)
(x, -y, z)
O
x
y
z
P(x,y,z)
P1
3.点P(x , y , z) 关于坐标轴的对称点:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变
O
x
y
z
P(x,y,z)
P1
平面直角坐标系
新课探究3——空间两点间的距离公式
平面上两点间的距离公式是什么?
问题3:空间两点间的距离怎么求呢?
x
y
P2
x
y
(x2,y2)
O
1
1
1
?
P2
P1
(x1,y1)
?
P1
空间直角坐标系
z
x
y
O
P(x,y,z)
(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:
P`
(x,y,0)
z
x
y
O
P2(x2,y2,z2)
(2) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:
N
P1(x1,y1,z1)
M
H
解
原结论成立.
1、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等.
课堂检测
z
x
y
A
B
C
O
A`
D`
C`
B`
M
N
2、如图,正方体OABC-D`A`B`C`的棱长为a,|AN|=2|CN|,|BM|=2|MC`|,求|MN|的长.
课堂检测
小结&作业
本节课你收获了什么?
一、知识:
1个概念:
2个公式:
二、方法:
1个学习方法:
2个求点坐标的方法:
小 结
作 业
凡事欲其成功,必要付出代价:奋斗。
——爱默生
课堂检测
4.3 空间直角坐标系
人教A版 必修2 第四章
x
O
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
复习回顾1——数轴上的点
1.数轴Ox上的点A,用代数的方法怎样表示呢?
x
y
A
O
x
y
(x,y)
平面中的点可以用有序实数对(x,y)来表示点
复习回顾2——平面直角坐标系中的点
2.直角坐标平面上的点A,怎样表示呢?
平面直角坐标系
新课探究1——空间直角坐标系
平面直角坐标系的建立:
问题1:空间直角坐标系又如何建立呢?
x
y
O
空间直角坐标系
1、空间直角坐标系的建立
在空间取定一点O
从O出发引三条两两垂直的直线
选定某个长度作为单位长度
(原点)
(坐标轴)
右手系
作图:一般使
新课讲授
o
x
y
z
135°
135°
X
Y
Z
坐标平面:通过每两个坐标轴的平面
坐标原点O
坐标轴:x轴,y轴,z轴
2、相关概念:
新课讲授
平面直角坐标系
新课探究2——空间中点的坐标表示
平面上点的坐标(x,y)
问题2:空间中点的坐标如何表示?
x
y
P
x
y
(x,y)
O
1
1
1
?
P
空间直角坐标系
?
1
1
1
?
P
?
P0
x
y
z
P点坐标为
(x,y,z)
P1
方法一:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。
X
Y
对于空间任意一点P,怎么求它的坐标?
P
Q
R
y
x
z
1
1
P
?
1
?
对于空间任意一点P,怎么求它的坐标?
方法二:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。
P
O
y
x
z
C
D
练习1:写出点P的坐标
(1)DP=2,CP=4
P(2,4,0)
知识运用
P
O
y
x
z
P1
C
D
P(2,4,5)
练习1:写出点P的坐标
(2)DP1=2,CP1=4,P1P=5
知识运用
P
O
y
x
z
P1
P(2,4,-5)
知识运用
练习1:写出点P的坐标
(3)DP1=2,CP1=4,P1P=-5
C
D
y
x
?
O
z
1
1
1
?
?
?
A
B
C
?
D
E
F
?
?
练习2:在空间直角坐标系中描出下列各点,并说明这些点的位置 A(0,1,1),B(0,0,2),C(0,2,0),
D(1,0,3),E(2,2,0),F(1,0,0)
知识运用
知识运用
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
二、坐标平面内的点
一、坐标轴上的点
规律总结:
O
x
y
z
P(x,y,z)
1.点P(x , y , z) 在下列坐标平面中的射影点为:
(1)在xoy平面射影点为P1__________;
(2)在xoz平面射影点为P2__________;
(3)在yoz平面射影点为P3__________;
P1
P2
(x,y,0)
(x,0,z)
P3
(0,y,z)
变式练习——空间中点的射影点与对称点坐标
2.点P(x , y , z) 关于坐标平面的对称点:
(1)关于xoy平面对称的点P1为__________;
(2)关于yoz平面对称的点P2为__________;
(3)关于xoz平面对称的点P3为__________;
关于谁对称谁不变
(x,y,-z)
(-x,y,z)
(x, -y, z)
O
x
y
z
P(x,y,z)
P1
3.点P(x , y , z) 关于坐标轴的对称点:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变
O
x
y
z
P(x,y,z)
P1
平面直角坐标系
新课探究3——空间两点间的距离公式
平面上两点间的距离公式是什么?
问题3:空间两点间的距离怎么求呢?
x
y
P2
x
y
(x2,y2)
O
1
1
1
?
P2
P1
(x1,y1)
?
P1
空间直角坐标系
z
x
y
O
P(x,y,z)
(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:
P`
(x,y,0)
z
x
y
O
P2(x2,y2,z2)
(2) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:
N
P1(x1,y1,z1)
M
H
解
原结论成立.
1、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等.
课堂检测
z
x
y
A
B
C
O
A`
D`
C`
B`
M
N
2、如图,正方体OABC-D`A`B`C`的棱长为a,|AN|=2|CN|,|BM|=2|MC`|,求|MN|的长.
课堂检测
小结&作业
本节课你收获了什么?
一、知识:
1个概念:
2个公式:
二、方法:
1个学习方法:
2个求点坐标的方法:
小 结
作 业
凡事欲其成功,必要付出代价:奋斗。
——爱默生
课堂检测
