必修2 第四章 圆与方程 直线系与圆系方程的应用 课件 33张PPT
文档属性
| 名称 | 必修2 第四章 圆与方程 直线系与圆系方程的应用 课件 33张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 678.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
直线系方程与圆系方程的应用
福建省漳浦第一中学
(高一 数学必修2 人教A版2003课标)
主 讲:福建省漳浦第一中学 张丽萍
指导老师:福建省漳浦第一中学 蔡长宝
严谨 勤奋 求实 进取
一、直线系方程
具有某种共同性质的所有直线的集合称为直线系。
直线系方程的定义
它的方程称为直线系方程。
直线系方程的种类:
y
o
x
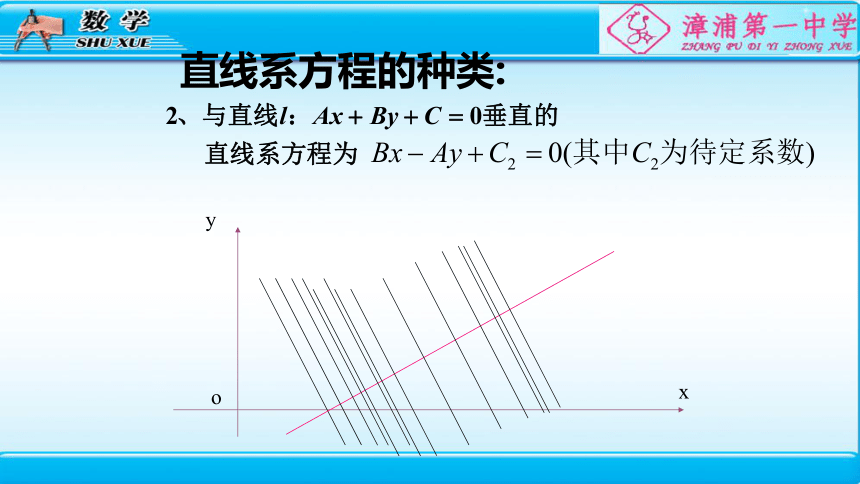
直线系方程的种类:
y
x
o
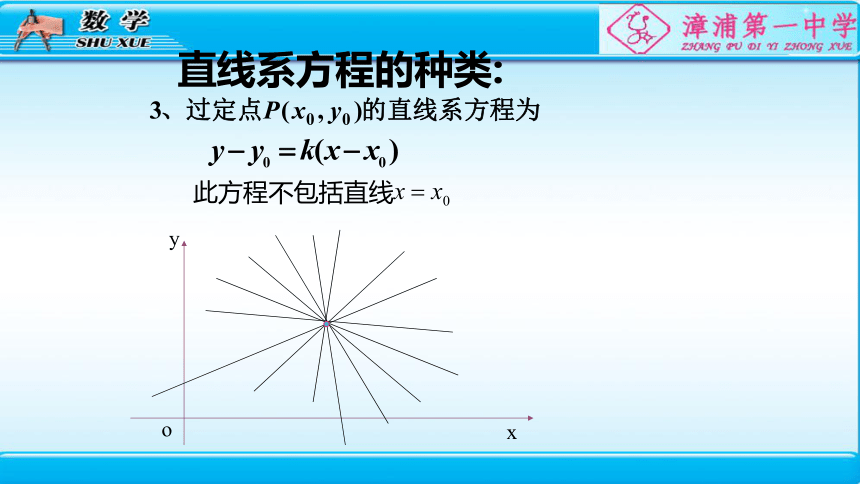
直线系方程的种类:
y
x
o
此方程不包括直线
4.过定点的直线系方程
如何表示经过两条相交直线交点的直线系方程?
相交,则过该交点的
已知直线 和直线
直线系方程为:
此方程不包括直线
此方程包括所有过
两直线交点的直线。
证明:
把(2,1)代入方程,得:
所以直线的方程为:
设经过两直线交点的直线方程为:
解法二:
解法一:联立方程组求出两条直线的交点坐标为
利用两点式可得到直线方程为 ,即
(1)求证:无论m取何实数,直线l 恒过定点,并求出定点坐标。
例题2.已知直线 ,
解:
整理该方程得:
法一
该方程表示过
交点的直线。
解方程组,得交点:
故无论m取何值,直线恒过定点
(1)求证:无论m取何实数,直线l 恒过定点,并求出定点坐标。
例题2.已知直线 ,
解:
从特殊到一般
法二
先由其中的两条特殊直线,求出交点
再证明其余直线均过此交点
分析:
分别令 代入方程,得
又因为: 恒成立
故无论m取何值,直线恒过定点
例题2:已知直线 ,
解:
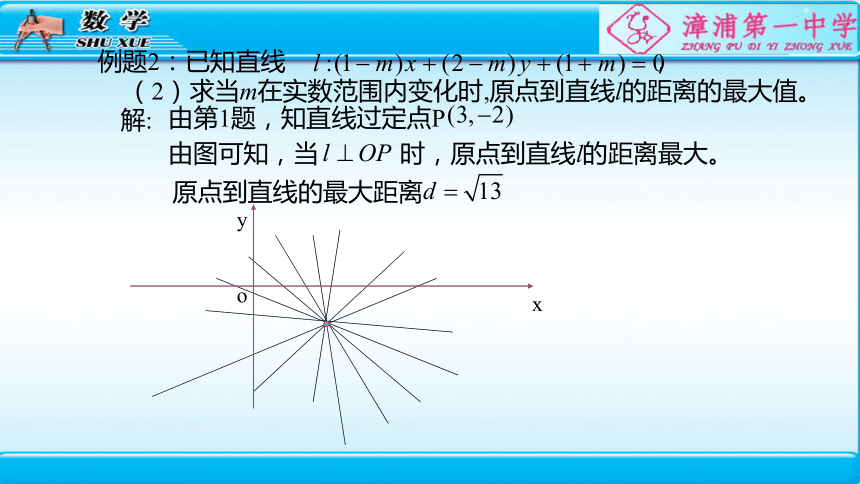
由图可知,当 时,原点到直线l的距离最大。
由第1题,知直线过定点P
原点到直线的最大距离
x
o
y
(2)求当m在实数范围内变化时,原点到直线l的距离的最大值。
例题2:已知直线 ,
(3)已知直线
解:
由第1题,知直线过定点
二、圆系方程
具有某种共同性质的圆的集合,称为圆系。
它的方程称为圆系方程.
圆系方程的定义
习题演练:已知 为坐标原点,直线 与圆
相交于 两点,若 ,求实数 的值.
解法一:这道题最易想到设出 ,由 得到 ,联立方程,由根与系数关系得出相关方程代入求解,最后验证.
依题意点 在以 为直径的圆上,则圆心 显然在直线l上,
则
又 满足方程 ①,则
解法二:设过直线 与圆 的交点的
圆系方程为
①
小结
1.直线系方程
2.圆系方程
在求解过直线与直线交点、直线与圆交点、圆与圆的交点的圆有关问题时,若能巧妙使用直线系与圆系方程,往往能优化解题过程,减少运算量,收到事半功倍的效果.
直线(圆)与圆的位置关系
圆系方程
直线(圆)与圆的位置关系
圆系方程
圆系方程
圆系方程
圆系方程
垂直
练 习 2
直线系方程
方程应有两非负根,故设
所以
解:
直线系方程
练 习 1
一. 已知直线分别满足下列条件,求直线的方程:
y=x
2x+3y-2=0
4x-3y-6=0
x+2y-11=0
直线系方程
直线(圆)与圆的位置关系
直线系方程与圆系方程的应用
福建省漳浦第一中学
(高一 数学必修2 人教A版2003课标)
主 讲:福建省漳浦第一中学 张丽萍
指导老师:福建省漳浦第一中学 蔡长宝
严谨 勤奋 求实 进取
一、直线系方程
具有某种共同性质的所有直线的集合称为直线系。
直线系方程的定义
它的方程称为直线系方程。
直线系方程的种类:
y
o
x
直线系方程的种类:
y
x
o
直线系方程的种类:
y
x
o
此方程不包括直线
4.过定点的直线系方程
如何表示经过两条相交直线交点的直线系方程?
相交,则过该交点的
已知直线 和直线
直线系方程为:
此方程不包括直线
此方程包括所有过
两直线交点的直线。
证明:
把(2,1)代入方程,得:
所以直线的方程为:
设经过两直线交点的直线方程为:
解法二:
解法一:联立方程组求出两条直线的交点坐标为
利用两点式可得到直线方程为 ,即
(1)求证:无论m取何实数,直线l 恒过定点,并求出定点坐标。
例题2.已知直线 ,
解:
整理该方程得:
法一
该方程表示过
交点的直线。
解方程组,得交点:
故无论m取何值,直线恒过定点
(1)求证:无论m取何实数,直线l 恒过定点,并求出定点坐标。
例题2.已知直线 ,
解:
从特殊到一般
法二
先由其中的两条特殊直线,求出交点
再证明其余直线均过此交点
分析:
分别令 代入方程,得
又因为: 恒成立
故无论m取何值,直线恒过定点
例题2:已知直线 ,
解:
由图可知,当 时,原点到直线l的距离最大。
由第1题,知直线过定点P
原点到直线的最大距离
x
o
y
(2)求当m在实数范围内变化时,原点到直线l的距离的最大值。
例题2:已知直线 ,
(3)已知直线
解:
由第1题,知直线过定点
二、圆系方程
具有某种共同性质的圆的集合,称为圆系。
它的方程称为圆系方程.
圆系方程的定义
习题演练:已知 为坐标原点,直线 与圆
相交于 两点,若 ,求实数 的值.
解法一:这道题最易想到设出 ,由 得到 ,联立方程,由根与系数关系得出相关方程代入求解,最后验证.
依题意点 在以 为直径的圆上,则圆心 显然在直线l上,
则
又 满足方程 ①,则
解法二:设过直线 与圆 的交点的
圆系方程为
①
小结
1.直线系方程
2.圆系方程
在求解过直线与直线交点、直线与圆交点、圆与圆的交点的圆有关问题时,若能巧妙使用直线系与圆系方程,往往能优化解题过程,减少运算量,收到事半功倍的效果.
直线(圆)与圆的位置关系
圆系方程
直线(圆)与圆的位置关系
圆系方程
圆系方程
圆系方程
圆系方程
垂直
练 习 2
直线系方程
方程应有两非负根,故设
所以
解:
直线系方程
练 习 1
一. 已知直线分别满足下列条件,求直线的方程:
y=x
2x+3y-2=0
4x-3y-6=0
x+2y-11=0
直线系方程
直线(圆)与圆的位置关系
