直线系圆系方程 课件 21张PPT
文档属性
| 名称 | 直线系圆系方程 课件 21张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
直线系圆系方程
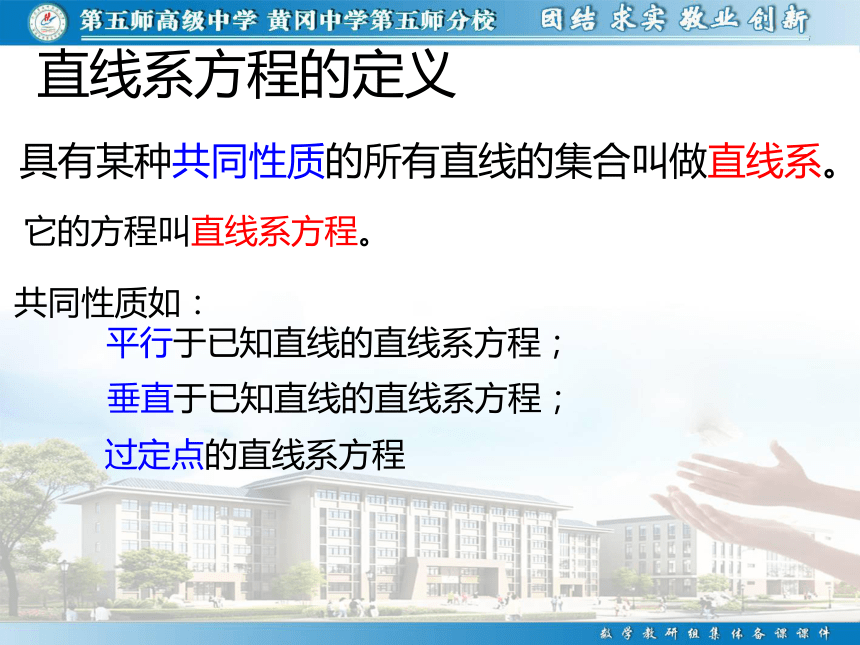
具有某种共同性质的所有直线的集合叫做直线系。
直线系方程的定义
它的方程叫直线系方程。
共同性质如:
平行于已知直线的直线系方程;
垂直于已知直线的直线系方程;
过定点的直线系方程
直线系方程的种类:
直线系方程
直线系方程的种类:
直线系方程
直线系方程的种类:
直线系方程
过定点的直线系方程
如何表示经过两条相交直线交点的直线系方程?
解:
整理该方程得:
【典型例题】
解:
【典型例题】
把(2,1)代入方程,得:
所以直线的方程为:
解(1):设经二直线交点的直线方程为:
直线系方程
直线系方程
解得:
由已知:
故所求得方程是:
解(2):将(1)中所设的方程变为:
练 习 1
一. 已知直线分别满足下列条件,求直线的方程:
y=x
2x+3y-2=0
4x-3y-6=0
x+2y-11=0
直线系方程
圆系方程
圆系方程
1、定义:具有某种 ______ 性质的圆叫做圆系;
它的方程叫 _____________
2、常见的圆系方程:
(1) 半径相等的圆系方程为
______________________________________
图象特点:_______________________
共同
圆系方程
( x -a ) 2 + ( y -b ) 2 = r 2 ( a、b 为参数 )
大小一样,位置不同
(2) 同心圆系方程为
___________________________________
图象特点:____________________
(3) 过两圆交点的圆系:若两圆 x 2 + y 2 + D1x +
E1y + F1 = 0 和 x 2 + y 2 + D2x + E2y + F2 = 0 相
交,则过这两圆交点的圆系方程为
________________________________________
( x -a ) 2 + ( y -b ) 2 = k 2 ( k 为参数 )
位置相同,大小不同
公共弦方程
故求两圆的公共弦方程,只需消去 x 2、y 2 项
例3、求过两圆 x 2 + y 2 -4x + 2y = 0
和 x 2 + y 2 -2y -4 = 0 的交点,
且圆心在直线 2x + 4y = 1上的圆方程。
解:设所求圆方程为
x 2 + y 2 -4x + 2y + ( x 2 + y 2 -2y -4 ) = 0
∴ x 2 + y 2 -3x + y -1 = 0
例4、求圆心为 ( 2 , 1 ) 且与已知圆 x 2 + y 2 -
3x = 0 的公共弦所在直线经过点 ( 5 , -2 ) 的
圆方程。
解:设所求圆为 x 2 + y 2 -4x -2y + F = 0
则公共弦方程: x + 2y -F = 0 过 ( 5 , -2 )
∴ F = 1
故 所求圆方程为 x 2 + y 2 -4x -2y + 1 = 0
例5、过直线 2x + y + 4 = 0 和圆 x 2 + y 2 + 2x -4y + 1
= 0 的交点,面积最小的圆方程
解:设所求圆方程为
x 2 + y 2 + 2x -4y + ( 2x + y + 4 ) = 0
故 所求圆为 5x 2 + 5y 2 + 26x -12y + 37 = 0
练习:
1、求过圆 x 2 + y 2 -6x -8y + 20 = 0 和 x 2 + y 2
-10x + 4y + 4 = 0 的交点,且过点 ( 3 , -1 ) 的
圆方程。
2、求过圆 x 2 + y 2-2y = 0 和直线 2x + y -3 = 0
的交点,且圆心在 x 轴上的圆方程。
(课后拓展题)3、求过圆 x 2 + y 2 = 4 和 x 2 + y 2-2x-4y + 4=0 的交点,且和直线 x + 2y = 0 相切的圆方程。
答案:
1、 x 2 + y 2 -8x -2y + 12 = 0
2、 x 2 + y 2 + 4x -6 = 0
3、 x 2 + y 2 -x -2y = 0 (课后拓展题答案)
圆系方程
课堂小结
圆系方程
作业布置:A组p132-133的4,10,11题
直线系圆系方程
具有某种共同性质的所有直线的集合叫做直线系。
直线系方程的定义
它的方程叫直线系方程。
共同性质如:
平行于已知直线的直线系方程;
垂直于已知直线的直线系方程;
过定点的直线系方程
直线系方程的种类:
直线系方程
直线系方程的种类:
直线系方程
直线系方程的种类:
直线系方程
过定点的直线系方程
如何表示经过两条相交直线交点的直线系方程?
解:
整理该方程得:
【典型例题】
解:
【典型例题】
把(2,1)代入方程,得:
所以直线的方程为:
解(1):设经二直线交点的直线方程为:
直线系方程
直线系方程
解得:
由已知:
故所求得方程是:
解(2):将(1)中所设的方程变为:
练 习 1
一. 已知直线分别满足下列条件,求直线的方程:
y=x
2x+3y-2=0
4x-3y-6=0
x+2y-11=0
直线系方程
圆系方程
圆系方程
1、定义:具有某种 ______ 性质的圆叫做圆系;
它的方程叫 _____________
2、常见的圆系方程:
(1) 半径相等的圆系方程为
______________________________________
图象特点:_______________________
共同
圆系方程
( x -a ) 2 + ( y -b ) 2 = r 2 ( a、b 为参数 )
大小一样,位置不同
(2) 同心圆系方程为
___________________________________
图象特点:____________________
(3) 过两圆交点的圆系:若两圆 x 2 + y 2 + D1x +
E1y + F1 = 0 和 x 2 + y 2 + D2x + E2y + F2 = 0 相
交,则过这两圆交点的圆系方程为
________________________________________
( x -a ) 2 + ( y -b ) 2 = k 2 ( k 为参数 )
位置相同,大小不同
公共弦方程
故求两圆的公共弦方程,只需消去 x 2、y 2 项
例3、求过两圆 x 2 + y 2 -4x + 2y = 0
和 x 2 + y 2 -2y -4 = 0 的交点,
且圆心在直线 2x + 4y = 1上的圆方程。
解:设所求圆方程为
x 2 + y 2 -4x + 2y + ( x 2 + y 2 -2y -4 ) = 0
∴ x 2 + y 2 -3x + y -1 = 0
例4、求圆心为 ( 2 , 1 ) 且与已知圆 x 2 + y 2 -
3x = 0 的公共弦所在直线经过点 ( 5 , -2 ) 的
圆方程。
解:设所求圆为 x 2 + y 2 -4x -2y + F = 0
则公共弦方程: x + 2y -F = 0 过 ( 5 , -2 )
∴ F = 1
故 所求圆方程为 x 2 + y 2 -4x -2y + 1 = 0
例5、过直线 2x + y + 4 = 0 和圆 x 2 + y 2 + 2x -4y + 1
= 0 的交点,面积最小的圆方程
解:设所求圆方程为
x 2 + y 2 + 2x -4y + ( 2x + y + 4 ) = 0
故 所求圆为 5x 2 + 5y 2 + 26x -12y + 37 = 0
练习:
1、求过圆 x 2 + y 2 -6x -8y + 20 = 0 和 x 2 + y 2
-10x + 4y + 4 = 0 的交点,且过点 ( 3 , -1 ) 的
圆方程。
2、求过圆 x 2 + y 2-2y = 0 和直线 2x + y -3 = 0
的交点,且圆心在 x 轴上的圆方程。
(课后拓展题)3、求过圆 x 2 + y 2 = 4 和 x 2 + y 2-2x-4y + 4=0 的交点,且和直线 x + 2y = 0 相切的圆方程。
答案:
1、 x 2 + y 2 -8x -2y + 12 = 0
2、 x 2 + y 2 + 4x -6 = 0
3、 x 2 + y 2 -x -2y = 0 (课后拓展题答案)
圆系方程
课堂小结
圆系方程
作业布置:A组p132-133的4,10,11题
