3.1 随机事件的概率小结 课件(共25张PPT)
文档属性
| 名称 | 3.1 随机事件的概率小结 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 702.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 11:18:40 | ||
图片预览





文档简介
(共25张PPT)
概率复习
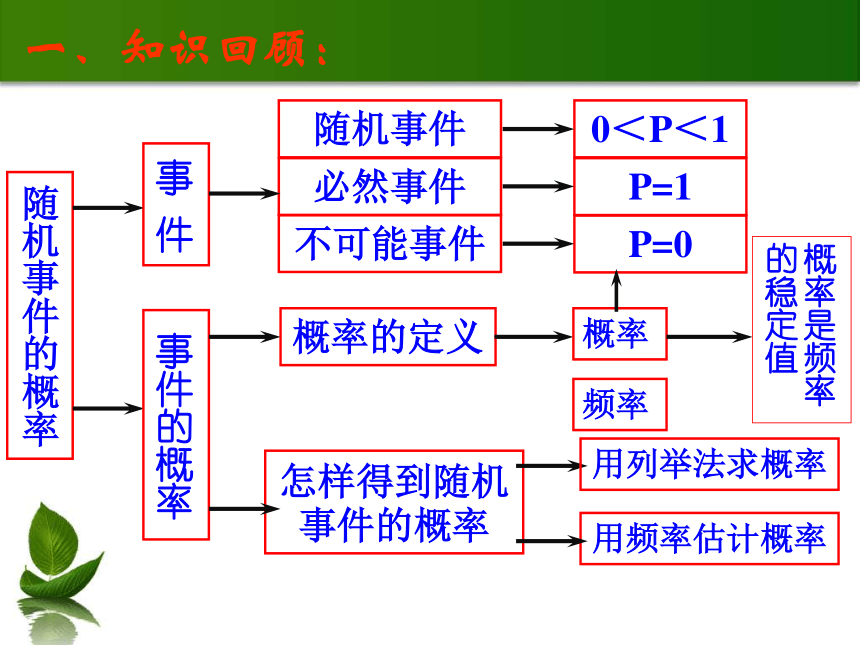
一、知识回顾:
随机事件的概率
事 件
事件的概率
随机事件
必然事件
不可能事件
概率的定义
怎样得到随机事件的概率
0<P<1
P=1
P=0
概率
频率
概率是频率的稳定值
用频率估计概率
用列举法求概率
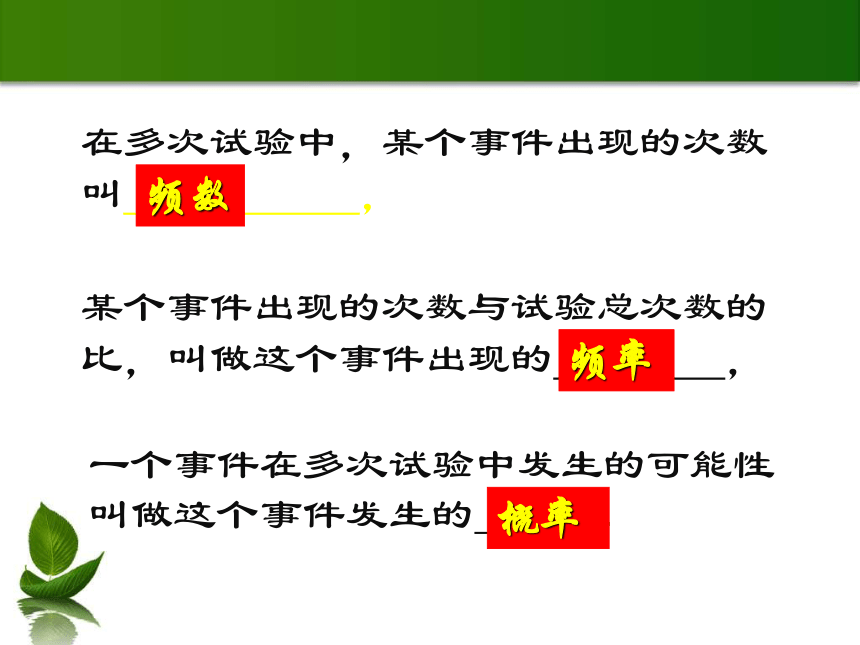
一个事件在多次试验中发生的可能性叫做这个事件发生的 。
在多次试验中,某个事件出现的次数
叫 ,
某个事件出现的次数与试验总次数的比,叫做这个事件出现的 ,
频数
频率
概率
区别:某可能事件发生的概率是一个定值.而这一事件发生的频率是波动的.当试验次数不大时,事件发生的频率与概率的差异甚至很大.
频率与概率的区别与联系
联系:当试验次数很大时,一个事件发生的频率稳定在相应的概率附近.即试验频率稳定于理论概率。因此:我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
注意:事件发生的频率不能简单地等同于
其概率
一般地,对于事件A和事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称 事件A包含于事件B),
记作:A B(或B A)
事件的关系与运算:
可用图表示为:
1、事件的包含关系
B
A
我们把不可能事件记作?,任何事件都包含不可能事件
一般地,若B A,且A B,那么称事件A与 事件B相等,记作:A=B。
2、事件的相等关系
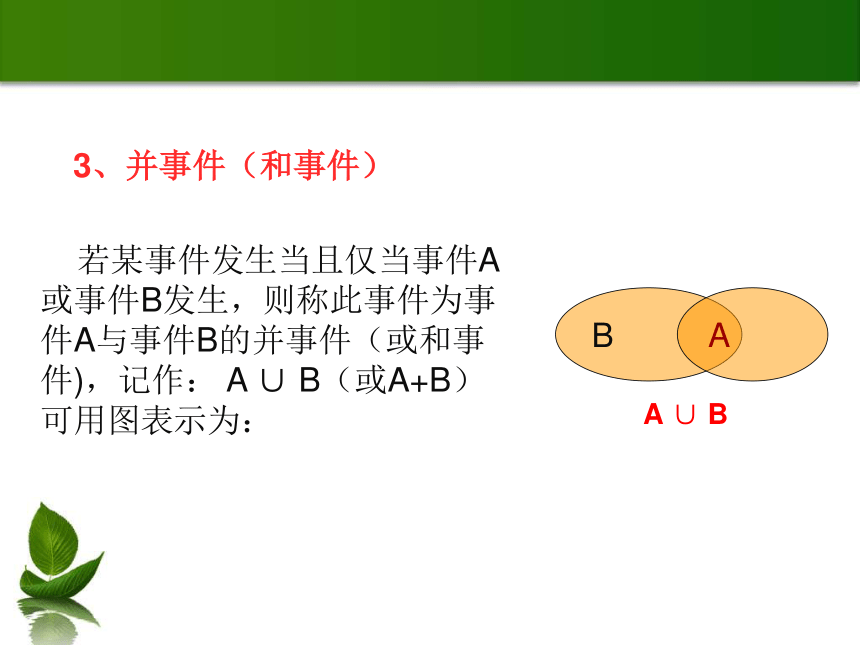
若某事件发生当且仅当事件A或事件B发生,则称此事件为事件A与事件B的并事件(或和事件),记作: A ∪ B(或A+B) 可用图表示为:
3、并事件(和事件)
B
A
A ∪ B
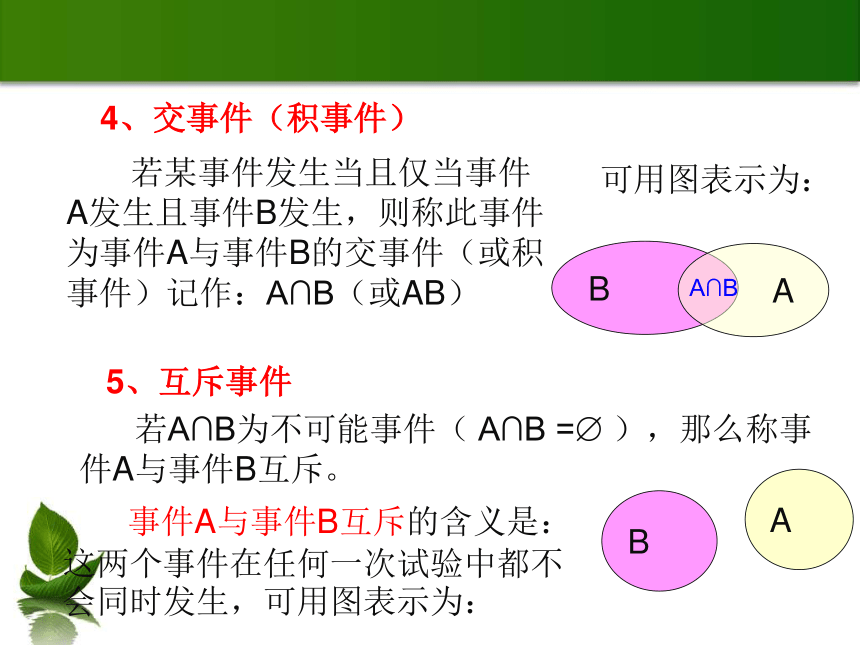
若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件)记作:A∩B(或AB)
4、交事件(积事件)
B
A
A∩B
可用图表示为:
若A∩B为不可能事件( A∩B =? ),那么称事 件A与事件B互斥。
事件A与事件B互斥的含义是:这两个事件在任何一次试验中都不会同时发生,可用图表示为:
5、互斥事件
B
A
若A∩B为不可能事件, A ∪ B为必然事件,那么 事件A与事件B互为对立事件。
事件A与事件B互为对立事件的含义是:这两个 事件在任何一次试验中有且仅有一个发生。
5、对立事件
互斥事件与对立事件的联系与区别:
1、两事件对立,必定互斥,但互斥未必对立
2、互斥的概念适用于多个事件,但对立概念只适用于两个事件
3、两个事件互斥只表明这两个事件不能同时发生,
即至多只能发生一个,但可以都不发生;
而两事件对立则表明它们有且只有一个发生
6、概率的加法公式
(1)当A、B是互斥事件时:
(2)当A、B是对立事件时:
求法:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
古典概型
古典概型的概率计算公式
古典概型问题,求概率的基本步骤
1、判断问题是否是古典概型
2、计算在一次实验中的所有可能结果n(基本事件总数)
3、计算属于事件A的基本事件数m
4、利用公式计算事件A的概率
在几何概型中,事件A的概率计算公式如下 :
P(A)=
几何概型
(1) 试验的基本事件有无限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为几何概率模型,简称几何概型。
几何概型问题,求概率的基本步骤
1、判断问题是否是几何概型
2、计算在一次实验中的表示所有可能结果的点(基本事件总数)围成的长度;(面积、体积)
3、计算表示属于事件A的基本事件的点围成的长度;面积、体积
4、利用公式计算事件A的概率
不同:古典概型要求基本事件有有限个,
几何概型要求基本事件有无限多个.
相同:两者基本事件的发生都是等可能的;
古典概型与几何概型的区别
1、甲乙两人下棋,两人下成和棋的概率是1/2,乙胜的概率是1/3,
则乙不输的概率是( )
甲获胜的概率是 ( )
甲不输的概率是 ( )
5/6
1/6
2/3
概率的基本性质
热身练习
2、同时掷两个骰子,出现点数之和大于11的概率是( )
3、如图所示,在矩形ABCD中,AB=4cm, BC=2cm,在图形上随机 地撒一粒黄豆,则黄豆落在阴影部分的概率 是
(π/8 )
古典概型
几何概型
1/36
典型例题
例1:柜子里装有3双不同的鞋,随机地取出2只,试求下列事件的概率
(1)取出的鞋子都是左脚的;
(2)取出的鞋子都是同一只脚的;
(1)记“取出的鞋子都是左脚的”为事件A 包含基本事件个数为 3 ,
(2)记“取出的鞋子都是同一只脚的”为事件B,
P( B)=
计算古典概型事件的概率 可分三步
①算出基本事件的总个数n,
②求出事件A所包含的基本事件个数m,
③代入公式求出概率P。
在计算基本事件总数和事件A包含的基本事件个数时,要做到不重不漏。
例1:柜子里装有3双不同的鞋,随机地取出2只,试求下列事件的概率
牛刀小试
【点评】
含有“至多”“至少”等类型的概率问题,
从正面 解决 比较困难或者比较繁琐时,
可考虑其反面,即对立事 件, 然后利用对立事件的性质进一步求解。
1.从装有2个红球和2个黑球的袋子中任取2个球,
那么互斥而不对立的事件是( )
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰有一个黑球与恰有两个黑球
D.至少有一个黑球与都是红球
随堂练习
2.在一个袋子中装有分别标注数字1, 2,3,4,5的
五个小球,现从中随机取出2个小球,则取出的
小球标注的数字之和为3或6的概率是
3/10
C
能力提升
某饮料公司对一名员工进行测试以便确定考评级别,公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中的3杯为A饮料,另外的2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料。若该员工3杯都选对,测评为优秀;若3杯选对2杯测评为良好;否则测评为合格。假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率
(2)求此人被评为良好及以上的概率
解:
将5不饮料编号为:1,2,3,4,5, 编号1,2,3表示A饮料, 编号
4 ,5表示B饮料,则从5杯饮料中选出3杯的所有可能情况为:
(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),
(1,4,5),( 2,3,4),(2,3,5),(2,4,5),(3,4,5)可见共
有10种
令D表示此人被评为优秀的事件,E表示此人被评人良好的事件,F表
示此人被评为良好及以上的事件。则
(1)P(D)=1/10
(2)P(E)=3/5 P(F)=P(D)+P(E)=7/10
综合检测
以下茎叶图记录了甲、乙两组个四名同学的植树个数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名
同学的植树总个数为19的概率.
解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为35/4,方差为11/16
(Ⅱ)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,
11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,
10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,
它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结
果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2)
故所求概率为 P(C)=4/16=1/4
课时小结
1、本节课主要复习了概率的基本性质,及古典概
型和几何概型的解题方法,区别与联系
2、 两种概率模型的特点:
①古典概型满足有限性和等可能性,
②几何概型满足无限性和等可能性,
3、两种概率模型的解题步骤:在具体求解时都是分三步。
①古典概型 :所求事件包含基本事件数 / 总基本事件数
②几何概型: 所求事件构成区域 / 总区域
谢谢观赏!
Thanks!
概率复习
一、知识回顾:
随机事件的概率
事 件
事件的概率
随机事件
必然事件
不可能事件
概率的定义
怎样得到随机事件的概率
0<P<1
P=1
P=0
概率
频率
概率是频率的稳定值
用频率估计概率
用列举法求概率
一个事件在多次试验中发生的可能性叫做这个事件发生的 。
在多次试验中,某个事件出现的次数
叫 ,
某个事件出现的次数与试验总次数的比,叫做这个事件出现的 ,
频数
频率
概率
区别:某可能事件发生的概率是一个定值.而这一事件发生的频率是波动的.当试验次数不大时,事件发生的频率与概率的差异甚至很大.
频率与概率的区别与联系
联系:当试验次数很大时,一个事件发生的频率稳定在相应的概率附近.即试验频率稳定于理论概率。因此:我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
注意:事件发生的频率不能简单地等同于
其概率
一般地,对于事件A和事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称 事件A包含于事件B),
记作:A B(或B A)
事件的关系与运算:
可用图表示为:
1、事件的包含关系
B
A
我们把不可能事件记作?,任何事件都包含不可能事件
一般地,若B A,且A B,那么称事件A与 事件B相等,记作:A=B。
2、事件的相等关系
若某事件发生当且仅当事件A或事件B发生,则称此事件为事件A与事件B的并事件(或和事件),记作: A ∪ B(或A+B) 可用图表示为:
3、并事件(和事件)
B
A
A ∪ B
若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件)记作:A∩B(或AB)
4、交事件(积事件)
B
A
A∩B
可用图表示为:
若A∩B为不可能事件( A∩B =? ),那么称事 件A与事件B互斥。
事件A与事件B互斥的含义是:这两个事件在任何一次试验中都不会同时发生,可用图表示为:
5、互斥事件
B
A
若A∩B为不可能事件, A ∪ B为必然事件,那么 事件A与事件B互为对立事件。
事件A与事件B互为对立事件的含义是:这两个 事件在任何一次试验中有且仅有一个发生。
5、对立事件
互斥事件与对立事件的联系与区别:
1、两事件对立,必定互斥,但互斥未必对立
2、互斥的概念适用于多个事件,但对立概念只适用于两个事件
3、两个事件互斥只表明这两个事件不能同时发生,
即至多只能发生一个,但可以都不发生;
而两事件对立则表明它们有且只有一个发生
6、概率的加法公式
(1)当A、B是互斥事件时:
(2)当A、B是对立事件时:
求法:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
古典概型
古典概型的概率计算公式
古典概型问题,求概率的基本步骤
1、判断问题是否是古典概型
2、计算在一次实验中的所有可能结果n(基本事件总数)
3、计算属于事件A的基本事件数m
4、利用公式计算事件A的概率
在几何概型中,事件A的概率计算公式如下 :
P(A)=
几何概型
(1) 试验的基本事件有无限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为几何概率模型,简称几何概型。
几何概型问题,求概率的基本步骤
1、判断问题是否是几何概型
2、计算在一次实验中的表示所有可能结果的点(基本事件总数)围成的长度;(面积、体积)
3、计算表示属于事件A的基本事件的点围成的长度;面积、体积
4、利用公式计算事件A的概率
不同:古典概型要求基本事件有有限个,
几何概型要求基本事件有无限多个.
相同:两者基本事件的发生都是等可能的;
古典概型与几何概型的区别
1、甲乙两人下棋,两人下成和棋的概率是1/2,乙胜的概率是1/3,
则乙不输的概率是( )
甲获胜的概率是 ( )
甲不输的概率是 ( )
5/6
1/6
2/3
概率的基本性质
热身练习
2、同时掷两个骰子,出现点数之和大于11的概率是( )
3、如图所示,在矩形ABCD中,AB=4cm, BC=2cm,在图形上随机 地撒一粒黄豆,则黄豆落在阴影部分的概率 是
(π/8 )
古典概型
几何概型
1/36
典型例题
例1:柜子里装有3双不同的鞋,随机地取出2只,试求下列事件的概率
(1)取出的鞋子都是左脚的;
(2)取出的鞋子都是同一只脚的;
(1)记“取出的鞋子都是左脚的”为事件A 包含基本事件个数为 3 ,
(2)记“取出的鞋子都是同一只脚的”为事件B,
P( B)=
计算古典概型事件的概率 可分三步
①算出基本事件的总个数n,
②求出事件A所包含的基本事件个数m,
③代入公式求出概率P。
在计算基本事件总数和事件A包含的基本事件个数时,要做到不重不漏。
例1:柜子里装有3双不同的鞋,随机地取出2只,试求下列事件的概率
牛刀小试
【点评】
含有“至多”“至少”等类型的概率问题,
从正面 解决 比较困难或者比较繁琐时,
可考虑其反面,即对立事 件, 然后利用对立事件的性质进一步求解。
1.从装有2个红球和2个黑球的袋子中任取2个球,
那么互斥而不对立的事件是( )
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰有一个黑球与恰有两个黑球
D.至少有一个黑球与都是红球
随堂练习
2.在一个袋子中装有分别标注数字1, 2,3,4,5的
五个小球,现从中随机取出2个小球,则取出的
小球标注的数字之和为3或6的概率是
3/10
C
能力提升
某饮料公司对一名员工进行测试以便确定考评级别,公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中的3杯为A饮料,另外的2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料。若该员工3杯都选对,测评为优秀;若3杯选对2杯测评为良好;否则测评为合格。假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率
(2)求此人被评为良好及以上的概率
解:
将5不饮料编号为:1,2,3,4,5, 编号1,2,3表示A饮料, 编号
4 ,5表示B饮料,则从5杯饮料中选出3杯的所有可能情况为:
(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),
(1,4,5),( 2,3,4),(2,3,5),(2,4,5),(3,4,5)可见共
有10种
令D表示此人被评为优秀的事件,E表示此人被评人良好的事件,F表
示此人被评为良好及以上的事件。则
(1)P(D)=1/10
(2)P(E)=3/5 P(F)=P(D)+P(E)=7/10
综合检测
以下茎叶图记录了甲、乙两组个四名同学的植树个数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名
同学的植树总个数为19的概率.
解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为35/4,方差为11/16
(Ⅱ)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,
11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,
10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,
它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结
果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2)
故所求概率为 P(C)=4/16=1/4
课时小结
1、本节课主要复习了概率的基本性质,及古典概
型和几何概型的解题方法,区别与联系
2、 两种概率模型的特点:
①古典概型满足有限性和等可能性,
②几何概型满足无限性和等可能性,
3、两种概率模型的解题步骤:在具体求解时都是分三步。
①古典概型 :所求事件包含基本事件数 / 总基本事件数
②几何概型: 所求事件构成区域 / 总区域
谢谢观赏!
Thanks!
