2020春北师大版九年级数学下册3.1圆-3.3垂径定理同步练习(3课时无答案)
文档属性
| 名称 | 2020春北师大版九年级数学下册3.1圆-3.3垂径定理同步练习(3课时无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 582.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 15:26:34 | ||
图片预览



文档简介
2020春北师大版九年级数学下册第三章圆3.1——3.3同步练习
3.1 圆
1.下列说法中,正确的是( )
A、弦是直径 B、半圆是弧
C、过圆心的线段是直径 D、圆心相同半径相同的两个圆是同心圆
2、如图,在⊙O中,点B、O、C和点A、O、D分别在同一条直线上,则图中有( )条弦
A. 2 B. 3 C. 4 D. 5
3、过圆内一点可以做圆的最长弦( )
A. 1条 B.2条 C. 3条 D. 4条
4、设⊙O的半径为r,P到圆心的距离为d不大于r,则点P在( )
A. 在⊙O内 B. 在⊙O外 C. 不在⊙O内 D.不在⊙O外
5、设⊙O的半径为5,圆心的坐标为(0,0),点 P的坐标为(4,-3),则点P在( )。
A. 在⊙O内 B. 在⊙O外 C. 在⊙O上 D.在⊙O内或外
6、如图点A、D、G、B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,NH=c,则下列说法正确的是( )
A. a>b>c B. a=b=c
C. c>a>b D. b>c>a
7、在⊿ABC中,∠C=90°,AB=3cm,BC=2cm,以点A为圆心,以2.5cm为半径作圆,则点C和⊙A的位置关系是( )
A.C在⊙A 上 B.C在⊙A 外 C.C在⊙A 内 D.C在⊙A 位置不能确定。
8、一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为( )
A.16cm或6cm, B.3cm或8cm C.3cm D.8cm
9、下列说法正确的是( )
A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧
C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧
10、(2008四川省资阳市)已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A、C、D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是
A.r>15 B.15<r<20 C.15<r<25 D.20<r<25
11、如图,在中,,,,是斜边上的中线,以为直径作⊙O,设线段的中点为,则点与⊙O的位置关系是( )
A.点在⊙O内 B.点在⊙O上C.点在⊙O外 D.无法确定
12、⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在 ,N点在圆 ,P点在圆 。
13、以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围。
14、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,
求∠A的度数.
15、如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,求∠ACD的度数.
16、如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.
17、已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点,
求证:AD=BC.
18、已知:如图点O是∠EPF的角平分线上的一点,以点O为圆心的圆和∠EPF的两边交于点A、B、C、D,求证:∠OBA=∠OCD
3.2 圆的对称性
1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
2.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
3.下列命题中,不正确的是( )
A.圆是轴对称图形 B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形 D.以上都不对
4.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等; D.以上说法都不对
5.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,,,则∠DAC的度数是( )
A. 70° B. 45° C. 35° D. 30°
6.一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
7.如图3,A、B、C、D是⊙上四点,且D是AB的中点,CD交OB于E,,= 度.
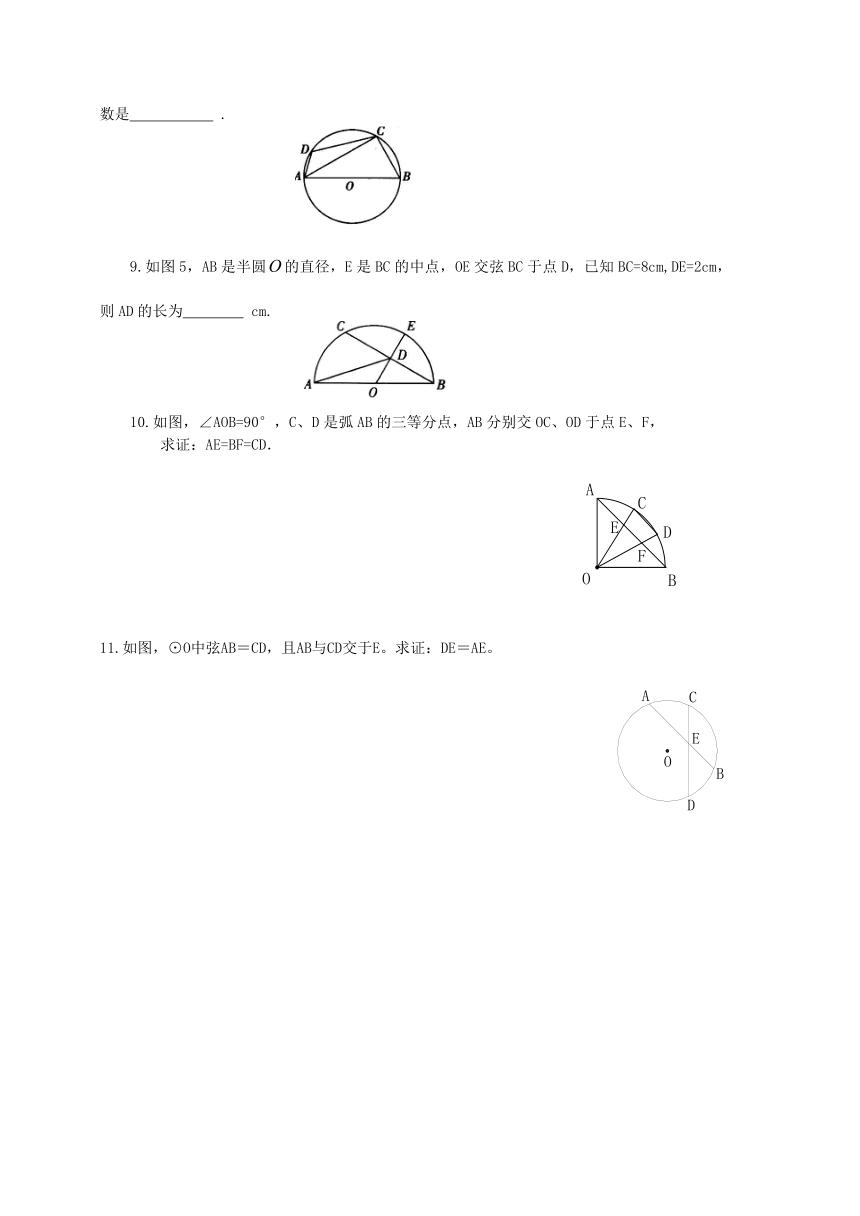
如图,已知AB是⊙的直径,C、D是⊙上的两点,,则的度数是 .
9.如图5,AB是半圆的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为 cm.
10.如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,
求证:AE=BF=CD.
11.如图,⊙O中弦AB=CD,且AB与CD交于E。求证:DE=AE。
*3.3 垂径定理
1.如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,则可推出的相等关系是___________.
2.圆中一条弦把和它垂直的直径分成3 cm和4 cm两部分,则这条弦弦长为__________.
3.判断正误.
(1)直径是圆的对称轴; (2)平分弦的直径垂直于弦.
4.圆O的半径OA=6,OA的垂直平分线交圆O于B、C,那么弦BC的长等于___________.
二、课中强化(10分钟训练)
1.圆是轴对称图形,它的对称轴是______________.
2.如图,在⊙O中,直径MN垂直于弦AB,垂足为C,图中相等的线段有__________,相等的劣弧有______________.
第2题图 第3题图
3.如图,弦AB的长为24 cm,弦心距OC=5 cm,则⊙O的半径R=__________ cm.
4.如图所示,直径为10 cm的圆中,圆心到弦AB的距离为4 cm.求弦AB的长.
三、课后巩固(30分钟训练)
1.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于( )
A.3 B.3 C. D.
第1题图 第2题图
2.如图24-1-2-6,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8 cm,OC=5 cm,则OD的长是( )
A.3 cm B.2.5 cm C.2 cm D.1 cm
3.⊙O半径为10,弦AB=12,CD=16,且AB∥CD.求AB与CD之间的距离.
4.如图所示,秋千链子的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面0.5 m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
5. “五段彩虹展翅飞”,我省利用国债资金修建的,横跨南渡江的琼州大桥如图(1)已于今年5月12日正式通车,该桥的两边均有五个红色的圆拱,如图(1).最高的圆拱的跨度为110米,拱高为22米,如图(2),那么这个圆拱所在圆的直径为___________米.
6.如图,要把破残的圆片复制完整,已知弧上三点A、B、C.
(1)用尺规作图法,找出弧BAC所在圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC为等腰三角形,底边BC=10 cm,腰AB=6 cm,求圆片的半径R;(结果保留根号)
(3)若在(2)题中的R满足n<R<m(m、n为正整数),试估算m和n的值.
7.⊙O的直径为10,弦AB的长为8,P是弦AB上的一个动点,求OP长的取值范围.
思路分析:求出OP长的最小值和最大值即得范围,本题考查垂径定理及勾股定理.该题创新点在于把线段OP看作是一个变量,在动态中确定OP的最大值和最小值.事实上只需作OM⊥AB,求得OM即可.
3.1 圆
1.下列说法中,正确的是( )
A、弦是直径 B、半圆是弧
C、过圆心的线段是直径 D、圆心相同半径相同的两个圆是同心圆
2、如图,在⊙O中,点B、O、C和点A、O、D分别在同一条直线上,则图中有( )条弦
A. 2 B. 3 C. 4 D. 5
3、过圆内一点可以做圆的最长弦( )
A. 1条 B.2条 C. 3条 D. 4条
4、设⊙O的半径为r,P到圆心的距离为d不大于r,则点P在( )
A. 在⊙O内 B. 在⊙O外 C. 不在⊙O内 D.不在⊙O外
5、设⊙O的半径为5,圆心的坐标为(0,0),点 P的坐标为(4,-3),则点P在( )。
A. 在⊙O内 B. 在⊙O外 C. 在⊙O上 D.在⊙O内或外
6、如图点A、D、G、B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,NH=c,则下列说法正确的是( )
A. a>b>c B. a=b=c
C. c>a>b D. b>c>a
7、在⊿ABC中,∠C=90°,AB=3cm,BC=2cm,以点A为圆心,以2.5cm为半径作圆,则点C和⊙A的位置关系是( )
A.C在⊙A 上 B.C在⊙A 外 C.C在⊙A 内 D.C在⊙A 位置不能确定。
8、一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为( )
A.16cm或6cm, B.3cm或8cm C.3cm D.8cm
9、下列说法正确的是( )
A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧
C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧
10、(2008四川省资阳市)已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A、C、D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是
A.r>15 B.15<r<20 C.15<r<25 D.20<r<25
11、如图,在中,,,,是斜边上的中线,以为直径作⊙O,设线段的中点为,则点与⊙O的位置关系是( )
A.点在⊙O内 B.点在⊙O上C.点在⊙O外 D.无法确定
12、⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在 ,N点在圆 ,P点在圆 。
13、以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围。
14、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,
求∠A的度数.
15、如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,求∠ACD的度数.
16、如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.
17、已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点,
求证:AD=BC.
18、已知:如图点O是∠EPF的角平分线上的一点,以点O为圆心的圆和∠EPF的两边交于点A、B、C、D,求证:∠OBA=∠OCD
3.2 圆的对称性
1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
2.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
3.下列命题中,不正确的是( )
A.圆是轴对称图形 B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形 D.以上都不对
4.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等; D.以上说法都不对
5.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,,,则∠DAC的度数是( )
A. 70° B. 45° C. 35° D. 30°
6.一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
7.如图3,A、B、C、D是⊙上四点,且D是AB的中点,CD交OB于E,,= 度.
如图,已知AB是⊙的直径,C、D是⊙上的两点,,则的度数是 .
9.如图5,AB是半圆的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为 cm.
10.如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,
求证:AE=BF=CD.
11.如图,⊙O中弦AB=CD,且AB与CD交于E。求证:DE=AE。
*3.3 垂径定理
1.如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,则可推出的相等关系是___________.
2.圆中一条弦把和它垂直的直径分成3 cm和4 cm两部分,则这条弦弦长为__________.
3.判断正误.
(1)直径是圆的对称轴; (2)平分弦的直径垂直于弦.
4.圆O的半径OA=6,OA的垂直平分线交圆O于B、C,那么弦BC的长等于___________.
二、课中强化(10分钟训练)
1.圆是轴对称图形,它的对称轴是______________.
2.如图,在⊙O中,直径MN垂直于弦AB,垂足为C,图中相等的线段有__________,相等的劣弧有______________.
第2题图 第3题图
3.如图,弦AB的长为24 cm,弦心距OC=5 cm,则⊙O的半径R=__________ cm.
4.如图所示,直径为10 cm的圆中,圆心到弦AB的距离为4 cm.求弦AB的长.
三、课后巩固(30分钟训练)
1.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于( )
A.3 B.3 C. D.
第1题图 第2题图
2.如图24-1-2-6,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8 cm,OC=5 cm,则OD的长是( )
A.3 cm B.2.5 cm C.2 cm D.1 cm
3.⊙O半径为10,弦AB=12,CD=16,且AB∥CD.求AB与CD之间的距离.
4.如图所示,秋千链子的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面0.5 m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
5. “五段彩虹展翅飞”,我省利用国债资金修建的,横跨南渡江的琼州大桥如图(1)已于今年5月12日正式通车,该桥的两边均有五个红色的圆拱,如图(1).最高的圆拱的跨度为110米,拱高为22米,如图(2),那么这个圆拱所在圆的直径为___________米.
6.如图,要把破残的圆片复制完整,已知弧上三点A、B、C.
(1)用尺规作图法,找出弧BAC所在圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC为等腰三角形,底边BC=10 cm,腰AB=6 cm,求圆片的半径R;(结果保留根号)
(3)若在(2)题中的R满足n<R<m(m、n为正整数),试估算m和n的值.
7.⊙O的直径为10,弦AB的长为8,P是弦AB上的一个动点,求OP长的取值范围.
思路分析:求出OP长的最小值和最大值即得范围,本题考查垂径定理及勾股定理.该题创新点在于把线段OP看作是一个变量,在动态中确定OP的最大值和最小值.事实上只需作OM⊥AB,求得OM即可.
