人教版高中数学必修5课件第二章2.4 等比数列(共19张PPT)
文档属性
| 名称 | 人教版高中数学必修5课件第二章2.4 等比数列(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 566.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 11:44:05 | ||
图片预览






文档简介
(共19张PPT)
等比数列
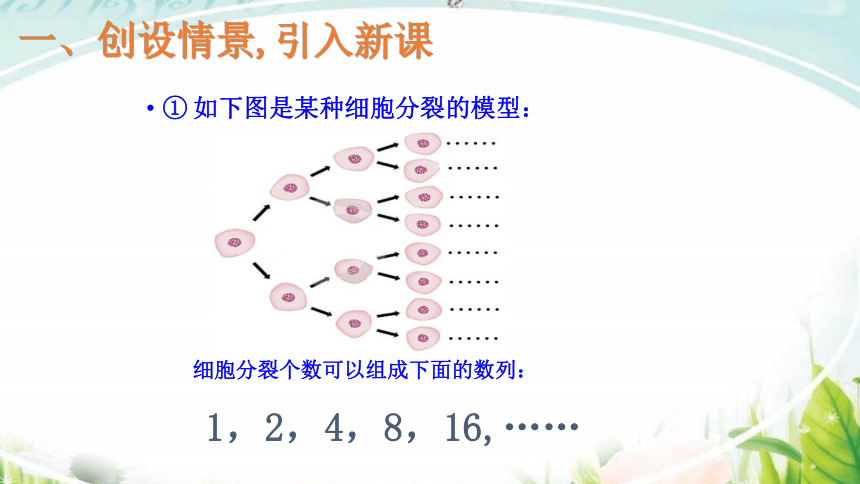
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
一、创设情景,引入新课
1,2,4,8,16,……
② 庄子曰:“一尺之棰,日取其半,万世不竭.”
意思:“一尺长的木棒,每日取其一半,永远也取不完” 。
如果将“一尺之棰”视为一份,则每日剩下的部分依次为:
③计算机病毒传播时,假设每一轮每一台计算机都感染20台计算机,则这种病毒每一轮感染的计算机数构成的数列是:
1,
20,
202,
203,
……
共同特点:
从第二项起,每一项与其前一项的比是同一个常数
对于数列①,从第2项起,每一项与前一项的比都等于__;
①
②
③
对于数列②,从第2项起,每一项与前一项的比都等于__;
对于数列①,从第2项起,每一项与前一项的比都等于__;
类比“等差数列”,这样的数列可以叫做“等比数列”。
二、引导探究,掌握新知
请问:这三个数列有什么共同特点?
其定义式:
1.等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个
数列就叫做等比数列。
比
2
同一个非零常数
这个常数叫做等比数列的公比,通常用字母q表示(q≠0)。
为什么要求q≠0?
或
判断一个数列是否为等比数列的依据
课堂互动
(1) 1,4,16,32,……
(3) 1,0,1,0,1,0,……
(4)
不是
(2) 1,-10,100,-1000,10000;
是,公比 q= -10
判定下列数列是否是等比数列?若是找出公比;不是,请说明理由。
不是等比数列
(5)
不是
2.等比数列的递推公式:
… …
1
1
-
=
n
n
q
a
a
… …
类比
3.等比数列的通项公式:
等差数列
等比数列
归纳法
思考:如何用 和 表示 ?
累乘法
……
共n – 1 项
×)
等比数列
方法:累加法
……
+)
等差数列
类比
思考:如何用 和 表示 ?
3.等比数列的通项公式:
4.等比中项
与等差数列概念类似,
若 成等比数列,那么G叫做 与 的等比中项,有:
注意:1)“ 成等比数列” 是 “ ”的
充分不必要条件
2)任意两个数 都有唯一等差中项为 ;
当 时,才有等比中项,且有两个 。
等比数列 名称 等差数列
概念
常数
定义式
通项公式
通项
变形
从第2项起,每一项与它前一项的比等同一个非零常数
从第2项起,每一项与它前一项的差等同一个常数
中项
公式
或
公比
公差
类 比
三、巩固新知----例题精讲
【例1】在等比数列 中:
(1)
(2)
(3)
题型一:等比数列的基本概念
(知三求一)
(基本量法或第二通项公式法)
三、巩固新知----例题精讲
题型二:等比中项
【例2】若在3和9之间插入两个正数,使前三个数成等比数列,后三个数成等差数列,求此二个数。
三、巩固新知----例题精讲
题型三:等比数列的判定和证明
【例3】数列 的通项公式为 ,求证数列
是等比数列。
名称 等比数列
概念
常数
定义式
通项公式
通项
变形
从第2项起,每一项与它前一项的比等于 同一个非零常数
中项
公式
课堂小结:
公比
或
【变式与拓展】
已知数列{an}满足 =1,an+1=2an+1.
(1)求证:数列{an+1}是等比数列;
(2)求{an}的通项公式.
thanks
等比数列
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
一、创设情景,引入新课
1,2,4,8,16,……
② 庄子曰:“一尺之棰,日取其半,万世不竭.”
意思:“一尺长的木棒,每日取其一半,永远也取不完” 。
如果将“一尺之棰”视为一份,则每日剩下的部分依次为:
③计算机病毒传播时,假设每一轮每一台计算机都感染20台计算机,则这种病毒每一轮感染的计算机数构成的数列是:
1,
20,
202,
203,
……
共同特点:
从第二项起,每一项与其前一项的比是同一个常数
对于数列①,从第2项起,每一项与前一项的比都等于__;
①
②
③
对于数列②,从第2项起,每一项与前一项的比都等于__;
对于数列①,从第2项起,每一项与前一项的比都等于__;
类比“等差数列”,这样的数列可以叫做“等比数列”。
二、引导探究,掌握新知
请问:这三个数列有什么共同特点?
其定义式:
1.等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个
数列就叫做等比数列。
比
2
同一个非零常数
这个常数叫做等比数列的公比,通常用字母q表示(q≠0)。
为什么要求q≠0?
或
判断一个数列是否为等比数列的依据
课堂互动
(1) 1,4,16,32,……
(3) 1,0,1,0,1,0,……
(4)
不是
(2) 1,-10,100,-1000,10000;
是,公比 q= -10
判定下列数列是否是等比数列?若是找出公比;不是,请说明理由。
不是等比数列
(5)
不是
2.等比数列的递推公式:
… …
1
1
-
=
n
n
q
a
a
… …
类比
3.等比数列的通项公式:
等差数列
等比数列
归纳法
思考:如何用 和 表示 ?
累乘法
……
共n – 1 项
×)
等比数列
方法:累加法
……
+)
等差数列
类比
思考:如何用 和 表示 ?
3.等比数列的通项公式:
4.等比中项
与等差数列概念类似,
若 成等比数列,那么G叫做 与 的等比中项,有:
注意:1)“ 成等比数列” 是 “ ”的
充分不必要条件
2)任意两个数 都有唯一等差中项为 ;
当 时,才有等比中项,且有两个 。
等比数列 名称 等差数列
概念
常数
定义式
通项公式
通项
变形
从第2项起,每一项与它前一项的比等同一个非零常数
从第2项起,每一项与它前一项的差等同一个常数
中项
公式
或
公比
公差
类 比
三、巩固新知----例题精讲
【例1】在等比数列 中:
(1)
(2)
(3)
题型一:等比数列的基本概念
(知三求一)
(基本量法或第二通项公式法)
三、巩固新知----例题精讲
题型二:等比中项
【例2】若在3和9之间插入两个正数,使前三个数成等比数列,后三个数成等差数列,求此二个数。
三、巩固新知----例题精讲
题型三:等比数列的判定和证明
【例3】数列 的通项公式为 ,求证数列
是等比数列。
名称 等比数列
概念
常数
定义式
通项公式
通项
变形
从第2项起,每一项与它前一项的比等于 同一个非零常数
中项
公式
课堂小结:
公比
或
【变式与拓展】
已知数列{an}满足 =1,an+1=2an+1.
(1)求证:数列{an+1}是等比数列;
(2)求{an}的通项公式.
thanks
