北师大版数学七年级第二学期第2章《相交线与平行线》单元测试卷(附详细答案)
文档属性
| 名称 | 北师大版数学七年级第二学期第2章《相交线与平行线》单元测试卷(附详细答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览

文档简介
北师大版七年级第二学期 第2章《相交线与平行线》单元测试卷
一.选择题(共10小题,满分30分)
1.三条直线相交,交点最多有( )
A.1个 B.2个 C.3个 D.4个
2.如图,直线AB、CD相交于点O,∠AOE=2∠AOC,若∠1=38°,则∠DOE等于( )
A.66° B.76° C.90° D.144°
3.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
4.如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=36°24′.则∠BOD的度数为( )
A.126°24′ B.53°36′ C.53°76′ D.36°24′
5.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是( )
A.PA B.PB C.PC D.PD
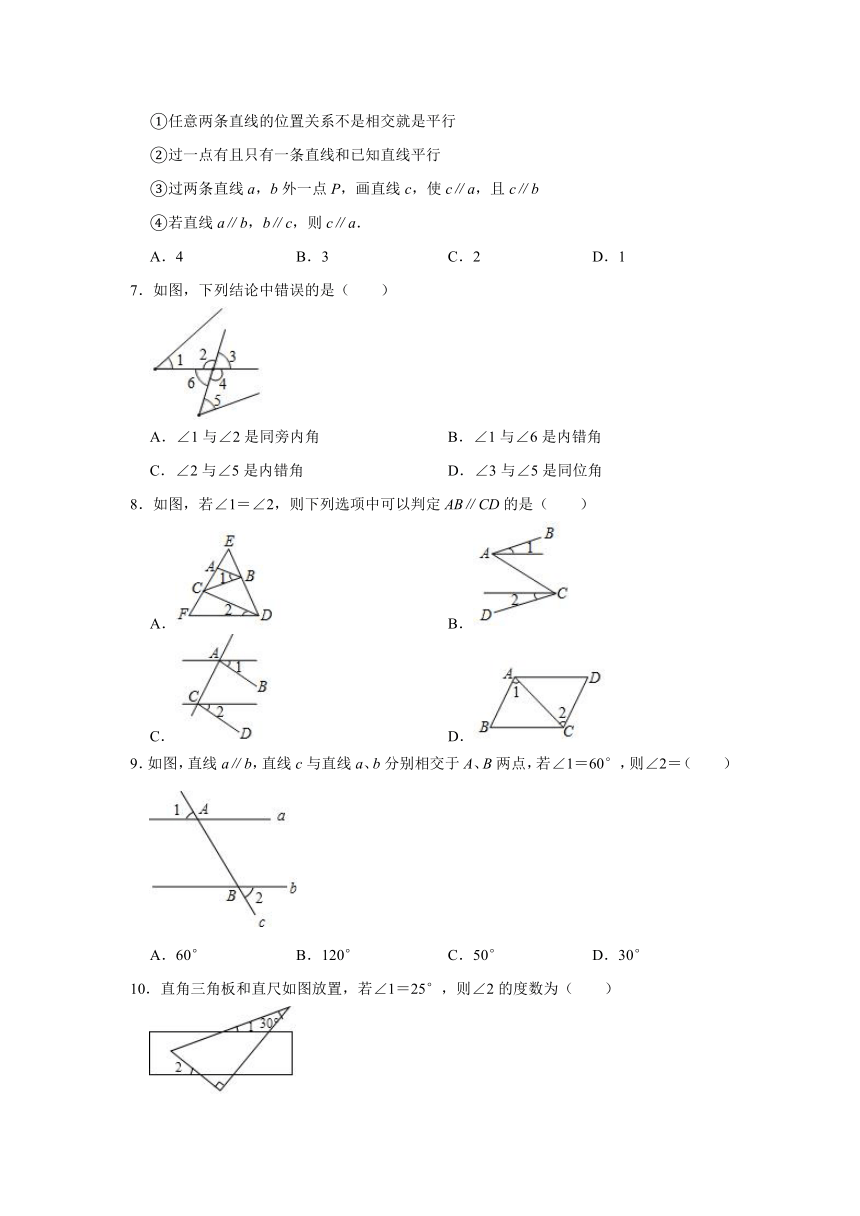
6.下列语句正确的有( )个
①任意两条直线的位置关系不是相交就是平行
②过一点有且只有一条直线和已知直线平行
③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b
④若直线a∥b,b∥c,则c∥a.
A.4 B.3 C.2 D.1
7.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
8.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A. B.
C. D.
9.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=( )
A.60° B.120° C.50° D.30°
10.直角三角板和直尺如图放置,若∠1=25°,则∠2的度数为( )
A.50° B.45° C.40° D.35°
二.填空题(共8小题,满分32分)
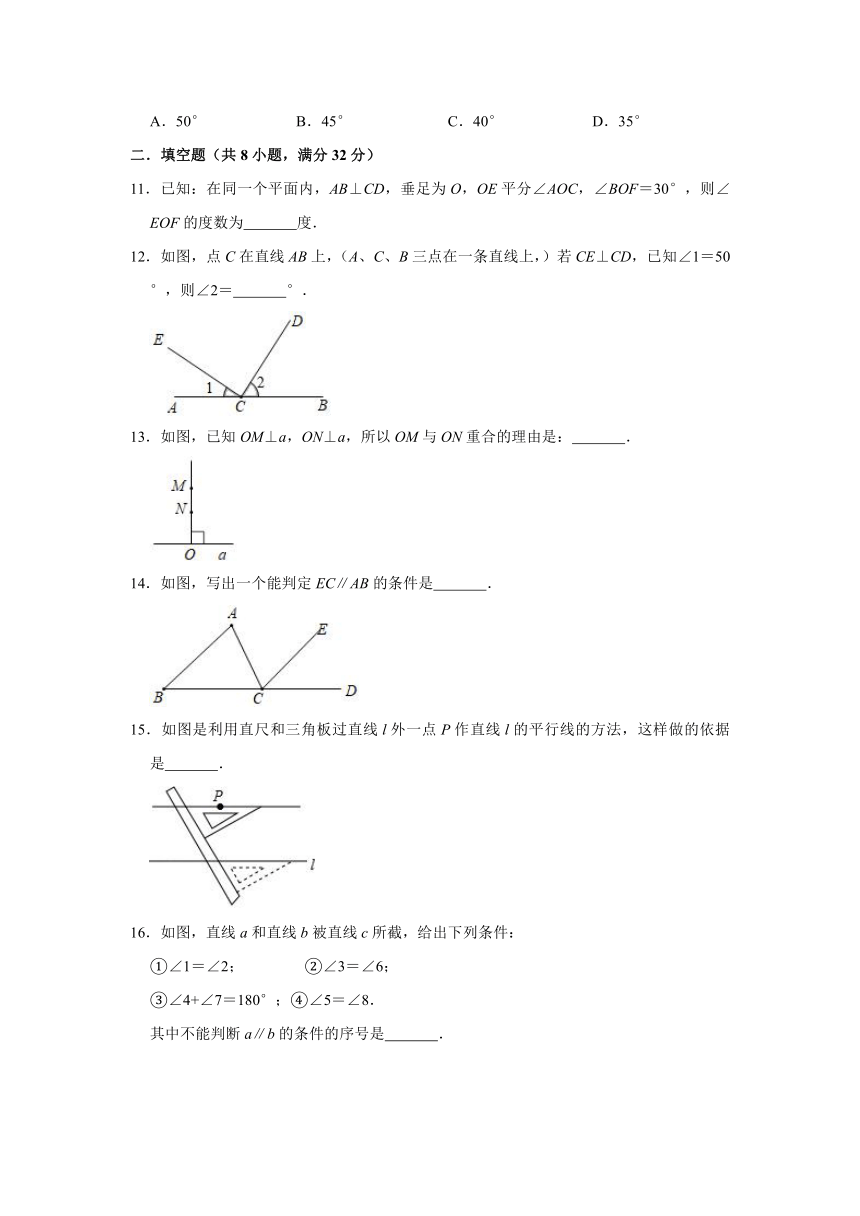
11.已知:在同一个平面内,AB⊥CD,垂足为O,OE平分∠AOC,∠BOF=30°,则∠EOF的度数为 度.
12.如图,点C在直线AB上,(A、C、B三点在一条直线上,)若CE⊥CD,已知∠1=50°,则∠2= °.
13.如图,已知OM⊥a,ON⊥a,所以OM与ON重合的理由是: .
14.如图,写出一个能判定EC∥AB的条件是 .
15.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
16.如图,直线a和直线b被直线c所截,给出下列条件:
①∠1=∠2; ②∠3=∠6;
③∠4+∠7=180°;④∠5=∠8.
其中不能判断a∥b的条件的序号是 .
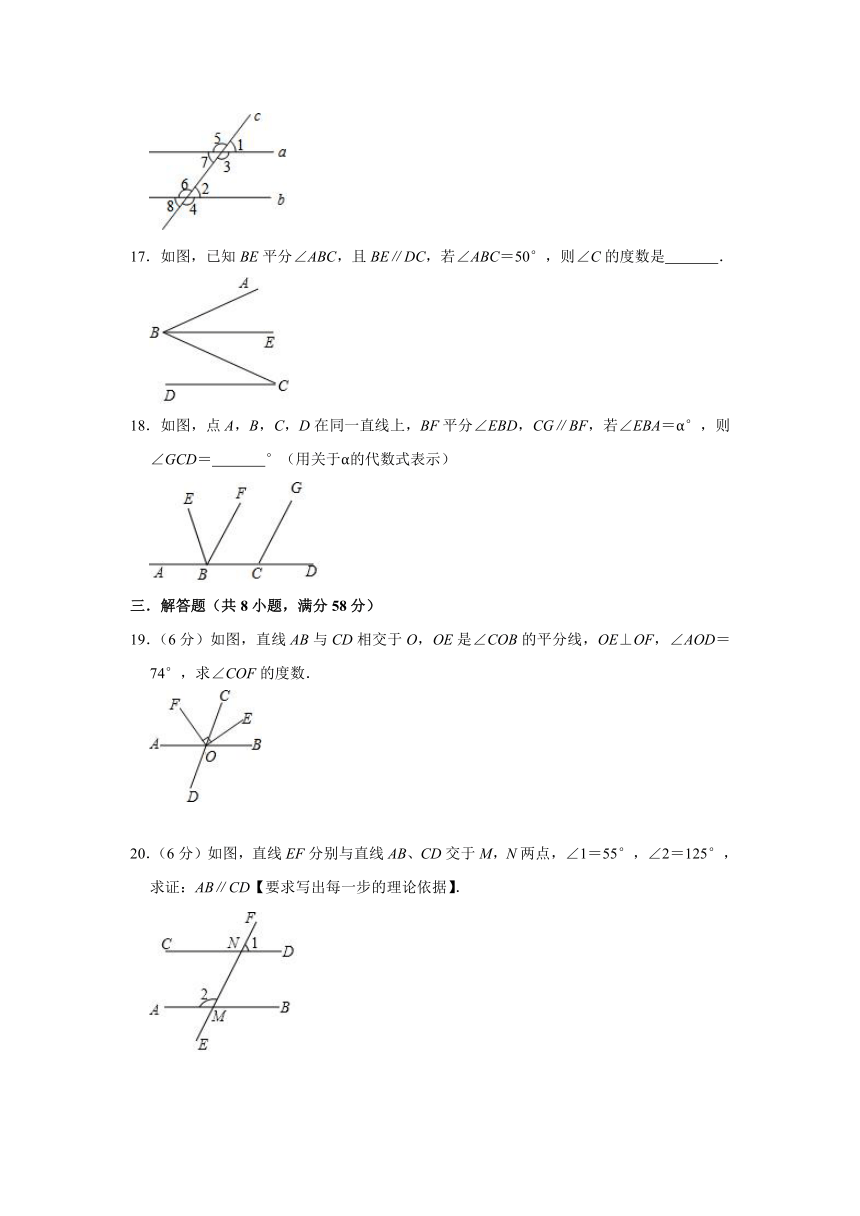
17.如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是 .
18.如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α°,则∠GCD= °(用关于α的代数式表示)
三.解答题(共8小题,满分58分)
19.(6分)如图,直线AB与CD相交于O,OE是∠COB的平分线,OE⊥OF,∠AOD=74°,求∠COF的度数.
20.(6分)如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
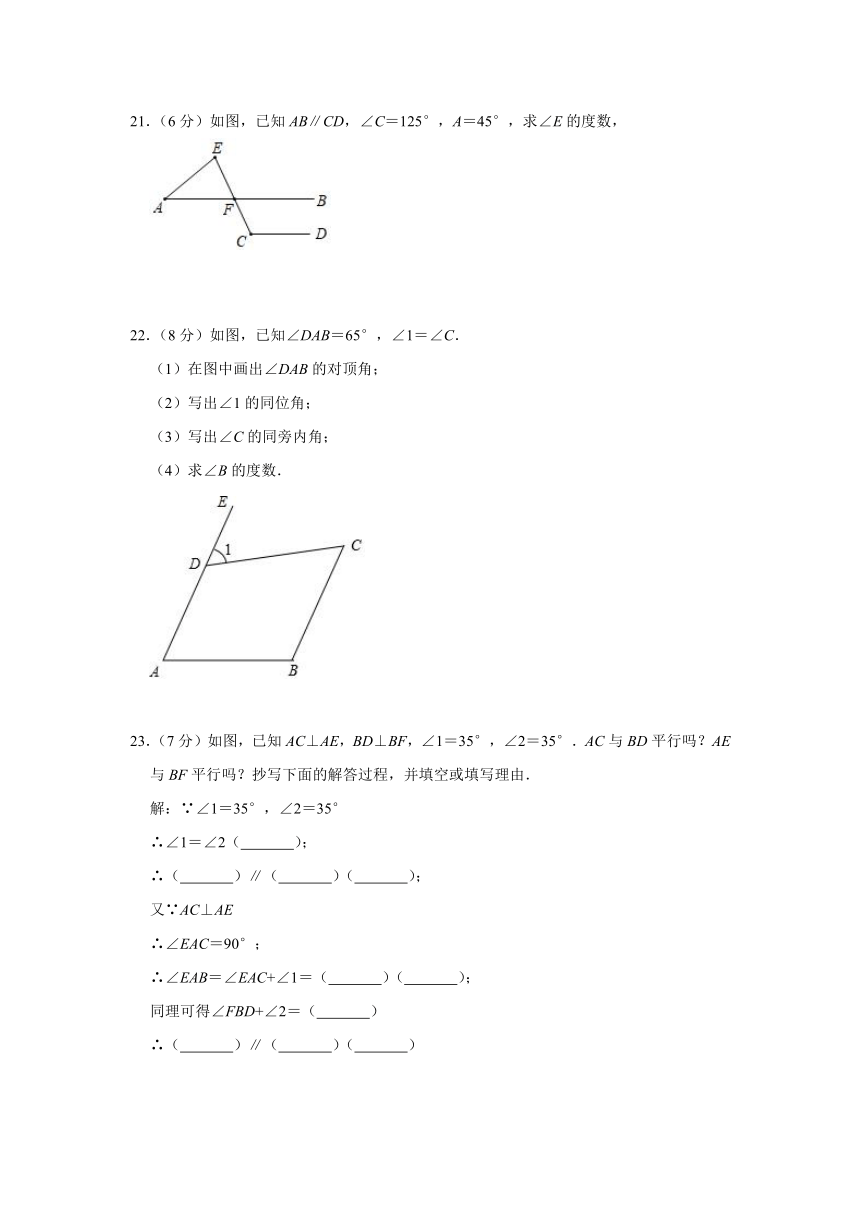
21.(6分)如图,已知AB∥CD,∠C=125°,A=45°,求∠E的度数,
22.(8分)如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
23.(7分)如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°.AC与BD平行吗?AE与BF平行吗?抄写下面的解答过程,并填空或填写理由.
解:∵∠1=35°,∠2=35°
∴∠1=∠2( );
∴( )∥( )( );
又∵AC⊥AE
∴∠EAC=90°;
∴∠EAB=∠EAC+∠1=( )( );
同理可得∠FBD+∠2=( )
∴( )∥( )( )
24.(7分)如图,直线AB、CD交直线MN于点E、F,过AB上的点H作HG⊥MN于点G,若∠EHG=27°,∠CFN=117°,判断直线AB、CD是否平行?并说明理由.
25.(9分)直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图①,若∠BOC=130°,求∠AOE的度数;
(2)如图②,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=∠DOF,求∠BOD的度数.
26.(9分)课上老师呈现一个问题:
下面提供三种思路:
思路一:过点F作MN∥CD(如图甲);
思路二:过P作PN∥EF,交AB于点N;
思路三:过O作ON∥FG,交CD于点N.
解答下列问题:
(1)根据思路一(图甲),可求得∠EFG的度数为 ;
(2)根据思路二、三分别在图乙和图丙中作出符合要求的辅助线;
(3)请你从思路二、思路三中任选其中一种,写出求∠EFG度数的解答过程.
参考答案
一.选择题(共10小题)
1.三条直线相交,交点最多有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:如图:
,
交点最多3个,
故选:C.
2.如图,直线AB、CD相交于点O,∠AOE=2∠AOC,若∠1=38°,则∠DOE等于( )
A.66° B.76° C.90° D.144°
【解答】解:如图,∠1=∠AOC=38°.
∵∠AOE=2∠AOC,
∴∠AOE=76°.
∴∠DOE=180°﹣∠AOC﹣∠AOE=180°﹣38°﹣76°=66°.
故选:A.
3.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
【解答】解:A、利用三角板画45°的角不符合尺规作图的定义,错误;
B、用直尺和三角板画平行线不符合尺规作图的定义,错误;
C、用直尺画一工件边缘的垂线不符合尺规作图的定义,错误;
D、用圆规在已知直线上截取一条线段等于已知线段符合尺规作图的定义,正确.
故选:D.
4.如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=36°24′.则∠BOD的度数为( )
A.126°24′ B.53°36′ C.53°76′ D.36°24′
【解答】解:∵EO⊥AB,
∴∠EOA=90°,
∵∠EOC=36°24′,
∴∠AOC=90°﹣36°24′=53°36′,
∴∠BOD=53°36′.
故选:B.
5.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是( )
A.PA B.PB C.PC D.PD
【解答】解:从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是PB,
故选:B.
6.下列语句正确的有( )个
①任意两条直线的位置关系不是相交就是平行
②过一点有且只有一条直线和已知直线平行
③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b
④若直线a∥b,b∥c,则c∥a.
A.4 B.3 C.2 D.1
【解答】解:①任意两条直线的位置关系不是相交就是平行,说法错误,应为根据同一平面内,任意两条直线的位置关系不是相交就是平行;
②过一点有且只有一条直线和已知直线平行,说法错误,应为过直线外一点有且只有一条直线和已知直线平行;
③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b,说法错误;
④若直线a∥b,b∥c,则c∥a,说法正确;
故选:D.
7.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
【解答】解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5是内错角,错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
8.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A. B.
C. D.
【解答】解:若∠1=∠2,则下列四个选项中,能够判定AB∥CD的是D,
故选:D.
9.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=( )
A.60° B.120° C.50° D.30°
【解答】解:∵直线a∥b,∠1=60°,
∴∠1=∠3=60°.
∵∠2与∠3是对顶角,
∴∠2=∠3=60°.
故选:A.
10.直角三角板和直尺如图放置,若∠1=25°,则∠2的度数为( )
A.50° B.45° C.40° D.35°
【解答】解:如图,过E作EF∥AB,
则AB∥EF∥CD,
∴∠3=∠1,∠2=∠4,
∵∠3+∠4=60°,
∴∠1+∠2=60°,
∵∠1=25°,
∴∠2=35°,
故选:D.
二.填空题(共8小题)
11.已知:在同一个平面内,AB⊥CD,垂足为O,OE平分∠AOC,∠BOF=30°,则∠EOF的度数为 105或165 度.
【解答】解:∵AB⊥CD,垂足为O,
∴∠AOC=∠COB=90°,
∵OE平分∠AOC,
∴∠AOE=∠COE=∠AOC=45°.
分两种情况:
①如图1,射线OF在∠BOC内部时,
∵∠AOE=45°,∠BOF=30°,
∴∠EOF=180°﹣∠AOE﹣∠BOF=105°;
②如图2,射线OF在∠BOD内部时,
∵∠COE=45°,∠COB=90°,∠BOF=30°,
∴∠EOF=∠COE+∠COB+∠BOF=165°.
故答案为105或165.
12.如图,点C在直线AB上,(A、C、B三点在一条直线上,)若CE⊥CD,已知∠1=50°,则∠2= 40 °.
【解答】解:∵CE⊥CD,
∴∠DOE=90°,
∵∠50°,
∴∠2=180°﹣90°﹣50°=40°,
故答案为:40.
13.如图,已知OM⊥a,ON⊥a,所以OM与ON重合的理由是: 在同一平面内,经过一点有且只有一条直线与已知直线垂直 .
【解答】解:∵OM⊥a,ON⊥a,
∴OM与ON重合(在同一平面内,经过一点有且只有一条直线与已知直线垂直),
故答案为:在同一平面内,经过一点有且只有一条直线与已知直线垂直.
14.如图,写出一个能判定EC∥AB的条件是 ∠A=∠ACE(答案不唯一) .
【解答】解:∵∠A=∠ACE,
∴EC∥AB(内错角相等,两直线平行).
故答案为:∠A=∠ACE(答案不唯一).
15.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 同位角相等,两直线平行 .
【解答】解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
16.如图,直线a和直线b被直线c所截,给出下列条件:
①∠1=∠2; ②∠3=∠6;
③∠4+∠7=180°;④∠5=∠8.
其中不能判断a∥b的条件的序号是 ④ .
【解答】解:①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③∠4+∠7=180°可得∠6+∠7=180°根据同旁内角互补,两直线平行得到a∥b;
④∠5=∠8不能判定a∥b;
故答案为:④.
17.如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是 25° .
【解答】解:∵BE平分∠ABC,∠ABC=50°,
∴∠ABE=∠EBC=25°,
∵BE∥DC,
∴∠C=∠EBC=25°.
故答案为:25°.
18.如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α°,则∠GCD= (90﹣α) °(用关于α的代数式表示)
【解答】解:∵∠EBA=α°,∠EBA+∠EBD=180°,
∴∠EBD=180°﹣α°,
∵BF平分∠EBD,
∴∠FBD=∠EBD=(180°﹣α°)=90°﹣α°,
∵CG∥BF,
∴∠FBD=∠GCD,
∴∠GCD=90°﹣α°=(90﹣α)°,
故答案为:(90﹣α).
三.解答题(共8小题)
19.如图,直线AB与CD相交于O,OE是∠COB的平分线,OE⊥OF,∠AOD=74°,求∠COF的度数.
【解答】解:∵∠AOD=70°,
∴∠BOC=70°,
∵OE是∠COB的平分线,
∴∠COE=∠COB=37°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°﹣37°=53°.
20.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
【解答】证明:∵∠1=55°(已知),
∴∠CNM=55°(对顶角相等),
∵∠2=125°(已知),
∴∠CNM+∠2=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
21.如图,已知AB∥CD,∠C=125°,A=45°,求∠E的度数,
【解答】解:∵直线AB∥CD,∠C=125°,
∴∠1=∠C=125°,
∵∠1=∠A+∠E,∠A=45°,
∴∠E=∠1﹣∠A=125°﹣45°=80°.
22.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
【解答】解:(1)如图,∠GAH即为所求;
(2)∠1的同位角是∠DAB;
(3)∠C的同旁内角是∠B和∠ADC;
(4)因为∠1=∠C,
所以AE∥BC.
所以∠DAB+∠B=180°,
又因为∠DAB=65°,
所以∠B=115°.
23.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°.AC与BD平行吗?AE与BF平行吗?抄写下面的解答过程,并填空或填写理由.
解:∵∠1=35°,∠2=35°
∴∠1=∠2( 等量代换 );
∴( AC )∥( BD )( 同位角相等,两直线平行 );
又∵AC⊥AE
∴∠EAC=90°;
∴∠EAB=∠EAC+∠1=( 125° )( 等式的性质 );
同理可得∠FBD+∠2=( 125° )
∴( AE )∥( BF )( 同位角相等,两直线平行 )
【解答】解:∵∠1=35°,∠2=35°,
∴∠1=∠2(等量代换);
∴(AC)∥(BD)(同位角相等,两直线平行)
又∵AC⊥AE,
∴∠EAC=90°;
∴∠EAB=∠EAC+∠1=(125°)(等式的性质);
同理可得∠FBD+∠2=(125°).
∴(AE)∥(BF)(同位角相等,两直线平行).
24.如图,直线AB、CD交直线MN于点E、F,过AB上的点H作HG⊥MN于点G,若∠EHG=27°,∠CFN=117°,判断直线AB、CD是否平行?并说明理由.
【解答】解:结论:AB∥CD.
理由:∵HG⊥MN,
∴∠HGE=90°,
∵∠AEF=∠HGE+∠EHG=90°+27°=117°,∠CFN=117°,
∴∠CFN=∠AEF,
∴AB∥CD.
25.直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图①,若∠BOC=130°,求∠AOE的度数;
(2)如图②,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=∠DOF,求∠BOD的度数.
【解答】解:(1)∵∠BOC=130°,
∴∠AOD=∠BOC=150°,
∠BOD=180°﹣∠BOC=50°
∵OE平分∠BOD,
∴∠DOE=25°
∴∠AOE=∠AOD+∠DOE=155°.
答:∠AOE的度数为155°
(2)①OF是∠AOD的平分线,理由如下:
∵OF⊥OE,
∴∠EOF=90°
∴∠BOE+∠AOF=90°
∵OE平分∠BOD,
∴∠BOE=∠DOE
∴∠DOE+∠AOF=90°
∠DOE+∠DOF=90°
∴∠AOF=∠DOF
∴OF是∠AOD的平分线;
②∵∠AOF=∠DOF,
设∠DOF=3x,则∠AOF=∠5x,
∵OF平分∠AOE,
∴∠AOF=∠EOF=5x
∴∠DOE=2x
∵OE平分∠BOD,
∴∠BOD=4x
5x+3x+4x=180°
∴x=15°.
∴∠BOD=4x=60°.
答:∠BOD的度数为60°.
26.课上老师呈现一个问题:
下面提供三种思路:
思路一:过点F作MN∥CD(如图甲);
思路二:过P作PN∥EF,交AB于点N;
思路三:过O作ON∥FG,交CD于点N.
解答下列问题:
(1)根据思路一(图甲),可求得∠EFG的度数为 120° ;
(2)根据思路二、三分别在图乙和图丙中作出符合要求的辅助线;
(3)请你从思路二、思路三中任选其中一种,写出求∠EFG度数的解答过程.
【解答】解:(1)如图甲,过F作MN∥CD,
∵MN∥CD,∠1=30°,
∴∠2=∠1=30°,
∵AB∥CD,
∴AB∥MN,
∵AB⊥EF,
∴∠3=∠4=90°,
∴∠EFG=∠3+∠2=90°+30°=120°.
故答案为:120°;
(2)由图可得,乙同学辅助线的做法为过P作PN∥EF;丙同学辅助线的做法为过O作ON∥FG;
(3)若选择乙,理由如下:
如图乙,过P作PN∥EF,
∵PN∥EF,EF⊥AB,
∴∠ONP=∠EOB=90°,
∵AB∥CD,
∴∠NPD=∠ONP=90°,
又∵∠1=30°,
∴∠NPG=90°+30°=120°,
∵PN∥EF,
∴∠EFG=∠NPG=120°;
若选择丙,理由如下:
如图丙,过O作ON∥FG,
∵ON∥FG,∠1=30°,
∴∠PNO=∠1=30°,
∵AB∥CD,
∴∠BON=∠PNO=30°,
又∵EF⊥AB,
∴∠EON=∠EOB+∠BON=90°+30°=120°,
∵ON∥FG,
∴∠EFG=∠EON=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
