人教版八年级数学下册 17.2.2勾股定理的逆定理课件(第2课时 共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册 17.2.2勾股定理的逆定理课件(第2课时 共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览






文档简介
课件19张PPT。17.2 勾股定理的逆定理
第2课时 勾股定理逆定理的实际应用 本节课教学是在学生学习勾股定理逆定理的基础上,鼓励学生以勾股定理及逆定理的知识为载体建立数学模型,利用数学模型去解决实际问题。
本课中所需学生思考、探究及计算部分可由学生根据自身实际情况掌控(可先暂停,完成思考计算后再继续观看学习。)重点:
灵活应用勾股定理的逆定理解决实际问题.
难点:
培养学生的建模思想,进一步加深勾股定理与其逆定理之间关系的认识. 上节课我们学习了有关互逆定理的知识,勾股定理的逆定理是什么?你能准确的区分这两个定理吗?
勾股定理勾股定理的逆定理在Rt△ABC中,∠C=900 ,
a , b 为直角边c 为斜边。
三边存在a2+b2=c2 △ABC 中,a,b 为较短边,c 为最长边,满足a2+b2=c2判定△ABC是直角三角形,∠C=900。题设结论 判断以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;是∠ A=900是∠ B=900(3) a:b: c=2:3:4 _____ _____ ;不是 常见的勾股数有3,4,5; 5,12,13;
6,8,10; 7,24,25;
8,15,17; 9,40,41.
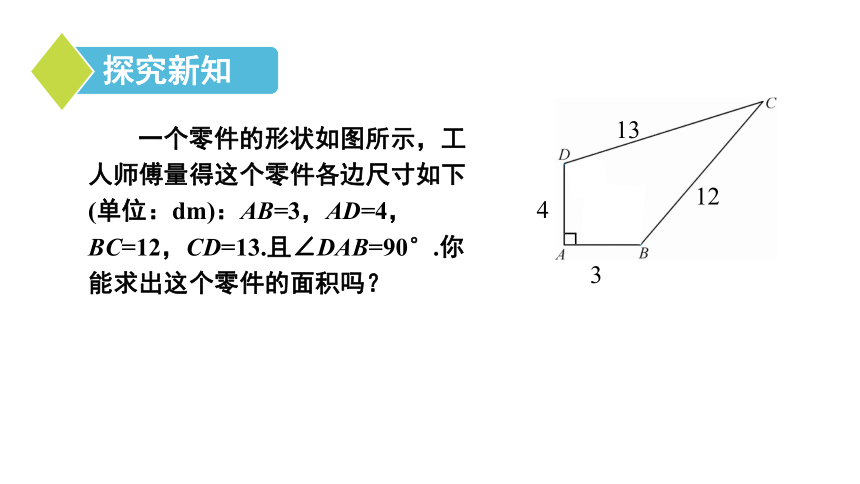
一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB=3,AD=4,BC=12,CD=13.且∠DAB=90°.你能求出这个零件的面积吗?341213┐∵CD=13 , BC=12∴∠DBC=90°在△BCD中解:连接BD
∵AB=3,AD=4∴BD= =5∴CD2=BC2+BD2∴△BCD是直角三角形∴S四边形ABCD=S△ABD+S△BCD = ×3×4+ ×5×12=36 答:这个零件的面积是36 dm2。 在Rt△ABD中341213┐5 点A是一个圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得AB=600m,AC=800m,问此公路是否会穿过该森林公园?1000600800BCA公园半径为400m影响因素:
1.公园的半径
2.点A到公路的距离
D过点A作AD⊥BC交BC于点D.?∴这条公路不会穿过自然保护区.∴AD=480解:在△ABC中∵AB2+AC2=6002+8002=10002=BC2.∴△ABC为直角三角形,∠BAC=90° ∵ 480>400
ABC例2 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海
天”号每小时航行12海里.它们离开
港口一个半小时后分别位于点Q、R
处,且相距30海里.如果知道“远航”
号沿东北方向航行,能知道“海天”
号沿哪个方向航行吗?解:根据题意,
PQ=16×1.5=24,PR=12×1.5=18 ,
QR=30 .∵ 242+182=302,即PQ 2+PR2=QR2, ∴ ∠QPR=90°由远航号沿东北方向航行可知∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行。如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国舰艇A发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国舰艇B密切注意.舰艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;舰艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?51213?解:设MN与AC相交于E,则∠BEC= 90°∵AB2+BC2=52+122=132=AC2,∴△ABC为直角三角形,且∠ABC= 90°.∵MN⊥CE,∴走私艇C进入我国领海的最短距离是CE.在Rt△EBC中△ABC中答:走私艇最早10时41分进入我国领海。E归纳:如何有效解决实际问题。1、构建对应几何图形。2、标注有用信息(或添加必要的辅助线),明确已知和所求。3、应用数学知识解决问题。1.已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是_ 度;2.△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为____;3.三角形的三边长为 8 ,15 ,17 ,那么最短边上的高为__;4.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三
角形的个数为( )
A 1个 B 2个 C 3个 D 4个5.在Rt△ABC中,斜边AB=1 ,
则 AB2 + BC2 + CA2 =____;6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则
2 CD2 + AD2 +BD2 =____;7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,此三角形为__三角形.8.工人师傅想要检测一扇小门两边 AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗? 9.三个半圆的面积分别为S1=3π,S2=4π,S3=7π,把三个半圆拼成如右图所示的图形,则△ABC一定是直角三角形吗? 如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
本课中所需学生思考、探究及计算部分可由学生根据自身实际情况掌控(可先暂停,完成思考计算后再继续观看学习。)重点:
灵活应用勾股定理的逆定理解决实际问题.
难点:
培养学生的建模思想,进一步加深勾股定理与其逆定理之间关系的认识. 上节课我们学习了有关互逆定理的知识,勾股定理的逆定理是什么?你能准确的区分这两个定理吗?
勾股定理勾股定理的逆定理在Rt△ABC中,∠C=900 ,
a , b 为直角边c 为斜边。
三边存在a2+b2=c2 △ABC 中,a,b 为较短边,c 为最长边,满足a2+b2=c2判定△ABC是直角三角形,∠C=900。题设结论 判断以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;是∠ A=900是∠ B=900(3) a:b: c=2:3:4 _____ _____ ;不是 常见的勾股数有3,4,5; 5,12,13;
6,8,10; 7,24,25;
8,15,17; 9,40,41.
一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB=3,AD=4,BC=12,CD=13.且∠DAB=90°.你能求出这个零件的面积吗?341213┐∵CD=13 , BC=12∴∠DBC=90°在△BCD中解:连接BD
∵AB=3,AD=4∴BD= =5∴CD2=BC2+BD2∴△BCD是直角三角形∴S四边形ABCD=S△ABD+S△BCD = ×3×4+ ×5×12=36 答:这个零件的面积是36 dm2。 在Rt△ABD中341213┐5 点A是一个圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得AB=600m,AC=800m,问此公路是否会穿过该森林公园?1000600800BCA公园半径为400m影响因素:
1.公园的半径
2.点A到公路的距离
D过点A作AD⊥BC交BC于点D.?∴这条公路不会穿过自然保护区.∴AD=480解:在△ABC中∵AB2+AC2=6002+8002=10002=BC2.∴△ABC为直角三角形,∠BAC=90° ∵ 480>400
ABC例2 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海
天”号每小时航行12海里.它们离开
港口一个半小时后分别位于点Q、R
处,且相距30海里.如果知道“远航”
号沿东北方向航行,能知道“海天”
号沿哪个方向航行吗?解:根据题意,
PQ=16×1.5=24,PR=12×1.5=18 ,
QR=30 .∵ 242+182=302,即PQ 2+PR2=QR2, ∴ ∠QPR=90°由远航号沿东北方向航行可知∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行。如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国舰艇A发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国舰艇B密切注意.舰艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;舰艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?51213?解:设MN与AC相交于E,则∠BEC= 90°∵AB2+BC2=52+122=132=AC2,∴△ABC为直角三角形,且∠ABC= 90°.∵MN⊥CE,∴走私艇C进入我国领海的最短距离是CE.在Rt△EBC中△ABC中答:走私艇最早10时41分进入我国领海。E归纳:如何有效解决实际问题。1、构建对应几何图形。2、标注有用信息(或添加必要的辅助线),明确已知和所求。3、应用数学知识解决问题。1.已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是_ 度;2.△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为____;3.三角形的三边长为 8 ,15 ,17 ,那么最短边上的高为__;4.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三
角形的个数为( )
A 1个 B 2个 C 3个 D 4个5.在Rt△ABC中,斜边AB=1 ,
则 AB2 + BC2 + CA2 =____;6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则
2 CD2 + AD2 +BD2 =____;7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,此三角形为__三角形.8.工人师傅想要检测一扇小门两边 AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗? 9.三个半圆的面积分别为S1=3π,S2=4π,S3=7π,把三个半圆拼成如右图所示的图形,则△ABC一定是直角三角形吗? 如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
