人教版高中数学必修5课件-3.2一元二次不等式及其解法(共17张PPT)
文档属性
| 名称 | 人教版高中数学必修5课件-3.2一元二次不等式及其解法(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 325.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
§3.2一元二次不等式及其解法
人教版高中数学必修5第三章
《不等式》
复习:一元二次方程与二次函数.
温故知新
(2)怎么画二次函数 y=ax2+bx+c(a≠0)的图像?
(1)一元二次方程ax2+bx+c=0(a≠0) 的解法有那些?
一元二次不等式及其解法
我们来考察二次函数
一元二次不等式的定义
思考:当y=0时,是什么?
当y>0或y<0时,这又是什么?
一元二次不等式的定义
只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
一元二次不等式的一般表达式为:
ax2+bx+c>0 或ax2+bx+c<0 (a≠0).
学习新知
一元二次不等式及其解法
思考:
那么一元二次不等式 怎样去求解呢?
一元二次不等式及其解法
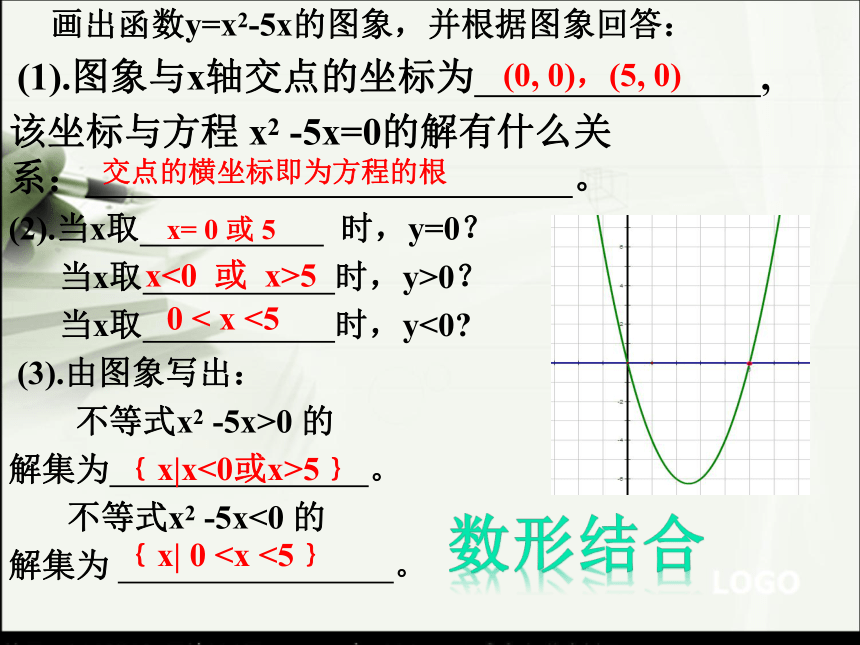
画出函数y=x2-5x的图象,并根据图象回答:
(1).图象与x轴交点的坐标为 ,
该坐标与方程 x2 -5x=0的解有什么关系: 。
(2).当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
(3).由图象写出:
不等式x2 -5x>0 的
解集为 。
不等式x2 -5x<0 的
解集为 。
(0, 0),(5, 0)
交点的横坐标即为方程的根
x= 0 或 5
x<0 或 x>5
0 < x <5
﹛x|x<0或x>5﹜
﹛x| 0
数形结合
推广:
1、 那么对于一般的不等式 ax2+bx+c>0 (a>0)或 ax2+bx+c<0 (a>0)又怎样去寻求解集呢?
2、讨论一元二次不等式ax2+bx+c>0 (a<0)或 ax2+bx+c<0 (a<0)的解集
一元二次不等式及其解法
特殊到一般
化未知到已知
总结出: 解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0 的步骤是:
(1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2) 写出ax2+bx+c=0判定△的符号,
(3)求出方程 的实根;画出函数图像
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
先求方程的根,
然后想像图象形状.
例1.解不等式
o
深化认识
一元二次不等式及其解法
先求方程的根,
然后想像图象形状.
例1.解不等式
o
深化认识
变式为:不等式
一元二次不等式及其解法
记忆口诀:
大于取两边,小于取中间.
一元二次不等式及其解法
这三者间有什么关系?
一元二次不等式
一元二次方程
二次函数
发现问题
一元二次函数、一元二次方程、一元二次不等式的关系
判别式
△=b2- 4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
x1
x2
x
y
O
y
x
O
x1
y
x
O
△>0
△=0
△<0
有两相异实根
x1, x2 (x1有两相等实根
x1=x2=
没有实根
{x|xx2}
{x|x1< xΦ
Φ
R
{x|x≠ }
解: 因为△= 16 -16 =0
方程 4 x2 - 4x +1=0 的解是
x1=x2=1/2
故原不等式的解集为{ x| x ≠ 1/2 }
(2)解不等式 - x2 + 2x – 3 >0
解:整理,得 x2 - 2x + 3 < 0
因为△= 4 - 12 = - 8 < 0
方程 2 x2 - 3x – 2 = 0无实数根
所以原不等式的解集为ф
例2、 (1) 解不等式4x2-4x +1>0
解:由于4x2-4x+1
=(2x-1)2≥0
深化认识
一元二次不等式及其解法
1.求下列一元二次不等式的解集:
(1) x2-x + 6<0;
(2) 4x2 - 4x + 1>0
(3) -x2+4x >6.
(4)(x -3)(x -7)<0
2.函数 的定义域是 ( )
A.{x|x≤-2,或x≥1};
B.{x|-2 C.{x|-2≤x≤1} ;
D.?.
课堂练习
A
一元二次不等式及其解法
一、知识点:
1.掌握三个二次的关系,注意结合函数图像,理解并会求一元二次不等式的解集
2.一元二次不等式解法步骤
二、数学思想方法:
1.数形结合
2.特殊到一般
3.化未知到已知
谈谈收获
一元二次不等式及其解法
课后作业:
必做题1:课本第80页练习1,2.
一元二次不等式及其解法
选做题2 :思考课本第80页习题A组第2、3、4题
§3.2一元二次不等式及其解法
人教版高中数学必修5第三章
《不等式》
复习:一元二次方程与二次函数.
温故知新
(2)怎么画二次函数 y=ax2+bx+c(a≠0)的图像?
(1)一元二次方程ax2+bx+c=0(a≠0) 的解法有那些?
一元二次不等式及其解法
我们来考察二次函数
一元二次不等式的定义
思考:当y=0时,是什么?
当y>0或y<0时,这又是什么?
一元二次不等式的定义
只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
一元二次不等式的一般表达式为:
ax2+bx+c>0 或ax2+bx+c<0 (a≠0).
学习新知
一元二次不等式及其解法
思考:
那么一元二次不等式 怎样去求解呢?
一元二次不等式及其解法
画出函数y=x2-5x的图象,并根据图象回答:
(1).图象与x轴交点的坐标为 ,
该坐标与方程 x2 -5x=0的解有什么关系: 。
(2).当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
(3).由图象写出:
不等式x2 -5x>0 的
解集为 。
不等式x2 -5x<0 的
解集为 。
(0, 0),(5, 0)
交点的横坐标即为方程的根
x= 0 或 5
x<0 或 x>5
0 < x <5
﹛x|x<0或x>5﹜
﹛x| 0
数形结合
推广:
1、 那么对于一般的不等式 ax2+bx+c>0 (a>0)或 ax2+bx+c<0 (a>0)又怎样去寻求解集呢?
2、讨论一元二次不等式ax2+bx+c>0 (a<0)或 ax2+bx+c<0 (a<0)的解集
一元二次不等式及其解法
特殊到一般
化未知到已知
总结出: 解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0 的步骤是:
(1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2) 写出ax2+bx+c=0判定△的符号,
(3)求出方程 的实根;画出函数图像
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
先求方程的根,
然后想像图象形状.
例1.解不等式
o
深化认识
一元二次不等式及其解法
先求方程的根,
然后想像图象形状.
例1.解不等式
o
深化认识
变式为:不等式
一元二次不等式及其解法
记忆口诀:
大于取两边,小于取中间.
一元二次不等式及其解法
这三者间有什么关系?
一元二次不等式
一元二次方程
二次函数
发现问题
一元二次函数、一元二次方程、一元二次不等式的关系
判别式
△=b2- 4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
x1
x2
x
y
O
y
x
O
x1
y
x
O
△>0
△=0
△<0
有两相异实根
x1, x2 (x1
x1=x2=
没有实根
{x|x
{x|x1< x
Φ
R
{x|x≠ }
解: 因为△= 16 -16 =0
方程 4 x2 - 4x +1=0 的解是
x1=x2=1/2
故原不等式的解集为{ x| x ≠ 1/2 }
(2)解不等式 - x2 + 2x – 3 >0
解:整理,得 x2 - 2x + 3 < 0
因为△= 4 - 12 = - 8 < 0
方程 2 x2 - 3x – 2 = 0无实数根
所以原不等式的解集为ф
例2、 (1) 解不等式4x2-4x +1>0
解:由于4x2-4x+1
=(2x-1)2≥0
深化认识
一元二次不等式及其解法
1.求下列一元二次不等式的解集:
(1) x2-x + 6<0;
(2) 4x2 - 4x + 1>0
(3) -x2+4x >6.
(4)(x -3)(x -7)<0
2.函数 的定义域是 ( )
A.{x|x≤-2,或x≥1};
B.{x|-2
D.?.
课堂练习
A
一元二次不等式及其解法
一、知识点:
1.掌握三个二次的关系,注意结合函数图像,理解并会求一元二次不等式的解集
2.一元二次不等式解法步骤
二、数学思想方法:
1.数形结合
2.特殊到一般
3.化未知到已知
谈谈收获
一元二次不等式及其解法
课后作业:
必做题1:课本第80页练习1,2.
一元二次不等式及其解法
选做题2 :思考课本第80页习题A组第2、3、4题
