人教版高中数学必修5课件-2.5 等比数列的前n项和(共15张PPT)
文档属性
| 名称 | 人教版高中数学必修5课件-2.5 等比数列的前n项和(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 505.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
课前三分钟
【文明 】:是社会进步的重要标志,也是社会主义现代化国家的重要特征。它是社会主义现代化国家文化建设的应有状态,是对面向现代化、面向世界面向未来的,民族的科学的大众的社会主义文化的概括,是实现中华民族伟大复兴的重要支撑。
?
【名言警句】人无礼不立,事无礼不成,国无礼不宁。——荀子
2.5 等比数列的前n项和
等差数列 等比数列
定义
通项公式
等差(等比)中项
下标和公式
Sn
Sn=
?
复习:
an-an-1=d(d为常 数,n≥2)
(q为常数n≥2)
an=a1+(n-1)d
an=am+(n-m)d
an=a1·qn-1(q≠0)
an=am·qn-m
A=
G=
若m+n=p+q,则
am+an=ap+aq
若m+n=p+q,则aman=apaq
某人听到一则消息,用一小时传给两个人,这两人用一小时每人又分别传给两人,如此传下去,一昼夜以后,这则消息能传遍一座千万人口的城市?
发现:
在第一小时后再昼夜内知道消息的人数构成一个等比数列:
数学小故事
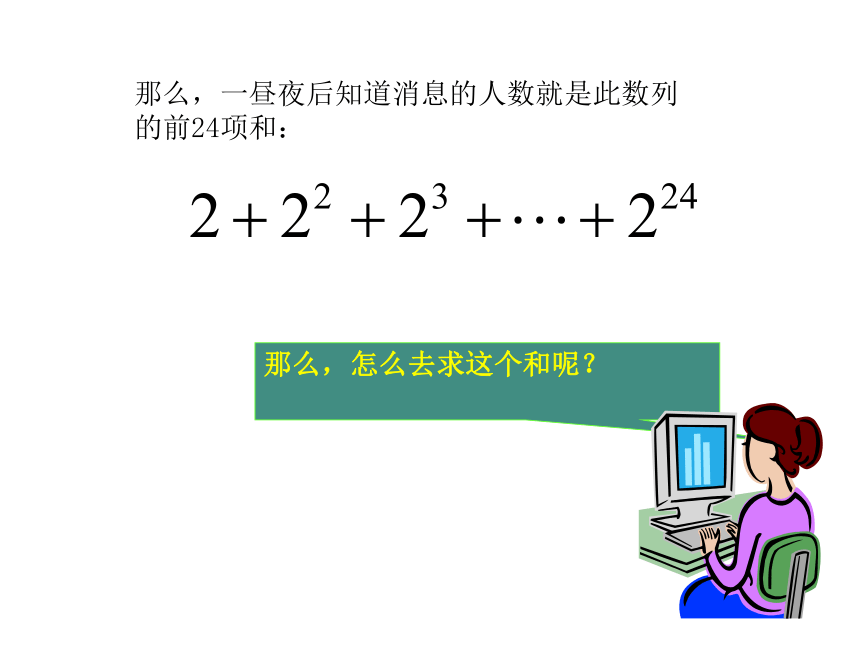
那么,一昼夜后知道消息的人数就是此数列的前24项和:
那么,怎么去求这个和呢?
一昼夜后知道信息的人数有多少呢?
这实际上是求首项为2,公比为2的等比数列的前24项的和。
33,554,430
=
这条消息,在一个昼夜就可被千万人口的城市的人知晓。
?
对于一般的等比数列我们将怎样求得它的前n项和呢?
两边同时乘以 为
设 为等比数列, 为首项, 为公比,它的前n项和
③
错位相减
4
由③- 得
4
分类讨论
当 时,
当 时,
?
即 是一个常数列
等比数列的通项公式
例1、求下列等比数列前8项的和
说明:
2.
1.
当
当
思考题1
思考题2:
求等比数列 1,2,4,…从第5项到第10项的和.
从第5项到第10项的和:
(1) 等比数列前n项和公式:
课堂小结
Sn=
{
1-q
(q=1)
(q=1)
Sn=
{
1-q
(q=1)
(q=1)
(2) 等比数列前n项和公式的应用:
1.在使用公式时.注意q的取值是利用公式的前提;
2.在使用公式时,要根据题意,适当选择公式。
等差数列 等比数列
定义
通项公式
等差(等比)中项
下标和公式
Sn
Sn=
an-an-1=d(d为常 数,n≥2)
(q为常数n≥2)
an=a1+(n-1)d
an=am+(n-m)d
an=a1·qn-1(q≠0)
an=am·qn-m
A=
G=
若m+n=p+q,则
am+an=ap+aq
若m+n=p+q,则aman=apaq
课后作业
P64习题2.5,A组第1、4、6题
课前三分钟
【文明 】:是社会进步的重要标志,也是社会主义现代化国家的重要特征。它是社会主义现代化国家文化建设的应有状态,是对面向现代化、面向世界面向未来的,民族的科学的大众的社会主义文化的概括,是实现中华民族伟大复兴的重要支撑。
?
【名言警句】人无礼不立,事无礼不成,国无礼不宁。——荀子
2.5 等比数列的前n项和
等差数列 等比数列
定义
通项公式
等差(等比)中项
下标和公式
Sn
Sn=
?
复习:
an-an-1=d(d为常 数,n≥2)
(q为常数n≥2)
an=a1+(n-1)d
an=am+(n-m)d
an=a1·qn-1(q≠0)
an=am·qn-m
A=
G=
若m+n=p+q,则
am+an=ap+aq
若m+n=p+q,则aman=apaq
某人听到一则消息,用一小时传给两个人,这两人用一小时每人又分别传给两人,如此传下去,一昼夜以后,这则消息能传遍一座千万人口的城市?
发现:
在第一小时后再昼夜内知道消息的人数构成一个等比数列:
数学小故事
那么,一昼夜后知道消息的人数就是此数列的前24项和:
那么,怎么去求这个和呢?
一昼夜后知道信息的人数有多少呢?
这实际上是求首项为2,公比为2的等比数列的前24项的和。
33,554,430
=
这条消息,在一个昼夜就可被千万人口的城市的人知晓。
?
对于一般的等比数列我们将怎样求得它的前n项和呢?
两边同时乘以 为
设 为等比数列, 为首项, 为公比,它的前n项和
③
错位相减
4
由③- 得
4
分类讨论
当 时,
当 时,
?
即 是一个常数列
等比数列的通项公式
例1、求下列等比数列前8项的和
说明:
2.
1.
当
当
思考题1
思考题2:
求等比数列 1,2,4,…从第5项到第10项的和.
从第5项到第10项的和:
(1) 等比数列前n项和公式:
课堂小结
Sn=
{
1-q
(q=1)
(q=1)
Sn=
{
1-q
(q=1)
(q=1)
(2) 等比数列前n项和公式的应用:
1.在使用公式时.注意q的取值是利用公式的前提;
2.在使用公式时,要根据题意,适当选择公式。
等差数列 等比数列
定义
通项公式
等差(等比)中项
下标和公式
Sn
Sn=
an-an-1=d(d为常 数,n≥2)
(q为常数n≥2)
an=a1+(n-1)d
an=am+(n-m)d
an=a1·qn-1(q≠0)
an=am·qn-m
A=
G=
若m+n=p+q,则
am+an=ap+aq
若m+n=p+q,则aman=apaq
课后作业
P64习题2.5,A组第1、4、6题
