四年级数学下册课件- 5.3 三角形的内角和 -人教新课标 (共36张PPT)
文档属性
| 名称 | 四年级数学下册课件- 5.3 三角形的内角和 -人教新课标 (共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 767.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 10:55:48 | ||
图片预览






文档简介
(共36张PPT)
人教版四年下册
三角形的内角和
由三条线段围成的图形叫做三角形.
角
角
角
边
边
边
顶点
顶点
顶点
旧知回顾:
已知∠1=300, ∠2=800,求∠3的度数。
300
800
?
旧知回顾:
正方形和长方形的内角和是多少度?
900
900
900
900
900
900
900
900
旧知回顾:
你的三边之和。是比我长,但三个内角之和并不比我大
我不但三边之和比你长,而且三个内角之和也比你大!
你同意谁的说法呢?为什么?
创设情境:
1:什么是三角形的内角?
2:三角形有几个内角?
3:什么是三角形的内角和?
自主探究:
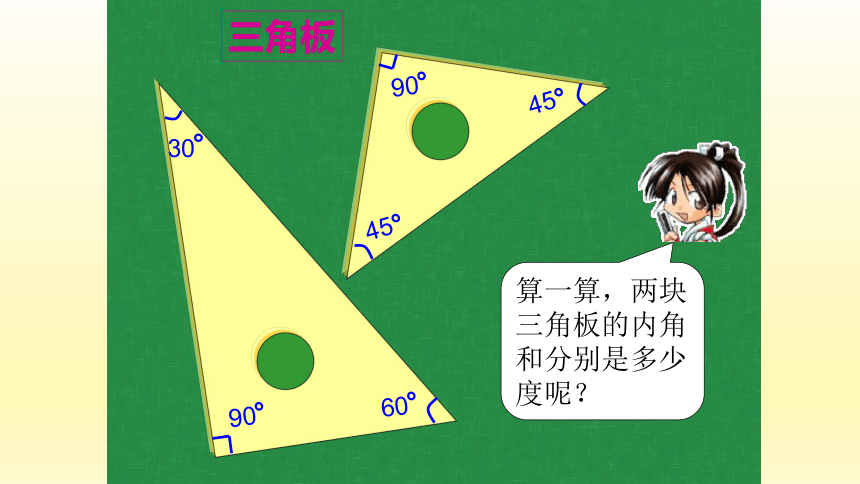
算一算,两块三角板的内角和分别是多少度呢?
30
45
45
60
90
90
三角板
大小、形状不同的三角形,它们的内角和一样吗?都是180?吗?
三角形按角分,可以分为哪几类?
猜一猜 想一想
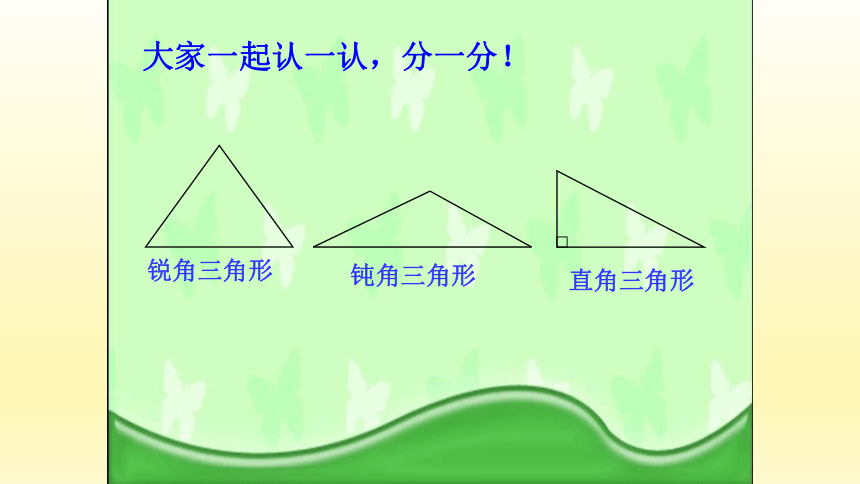
大家一起认一认,分一分!
锐角三角形
钝角三角形
直角三角形
小组活动:
(1)小组分工。
(2)同学们能通过动手操作,想办法来验证自己的猜想吗? 请同学们先独立思考想一想,再在小组内把你的想法与同伴进行交流,然后选用一种方法进行验证。
(3)最后要求计算出三个角的和是多少?填在表格里。
∠1 ∠2 ∠3 内角和 发现规律
锐角三角形
直角三角形
钝角三角形
分小组汇报交流
量一量
小组活动一:
撕一撕
拼一拼
小组活动二:
3
2
3
1
平角:1800
三角形的内角和是1800。
2
1
折一折
拼一拼
小组活动三:
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
得出结论:
三角形的内角和是1800。
在一个三角形中,已知∠1=1400,∠3=250,求∠2的度数?
1800-1400-250
=400-250
=150
答:∠2的度数为150。
内角和1800
做一做
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
分层训练:
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
1800-700×2
=1800 -1400
=400
1800-700 -700
=1100 -700
=400
700
700
400
内角和1800
答:它的顶角是400。
1800÷3=60°
(1800-960) ÷2
=840÷2
=42°
①1800-900-400
=900-400
=50°
我的一个角是多少度?
我的一个底角是多少度?
我是一个直角三角形,我的另一个锐角是多少度?
②900-400=50°
三角形∠1=140°∠3=25°求∠2的度数。
180°-140°-25°=15°
180 °-(140° +25°)=15 °
140°
25°
?
75°
35°
?
75°
35°
180° -75 ° - 35°=70°
180° -(75 ° + 35°)=70°
?
已知等腰三角形的风筝,一个底角70°,顶角多少度?
180°-70°-70°=40°
180°-70°×2=40°
70°
70°
?
180°-90°-50°=40°
180° -(50°+90°)=40 °
一个直角三角形,一个锐角是50°,另一个锐角是几度?
50°
90°-50°=40°
?
选择
1.下面每组三个角,不可能在同一个三角内的是( )。
A.15° 78° 87°B.55° 120° 5°C.90° 18° 102°
2.把一个三角形纸片剪成两个小三角形,每个小三角形的内角和( )180度。
A.大于 B.小于 C.等于
C
C
判断下列说法对吗?
①钝角三角形的内角和大于锐角三角形的内角和。(??? )
②在直角三角形中,两个锐角的和等于90 ?。(??? )
③在钝角三角形中,两个锐角的和大于90 ?。(??? )
④三角形中有一个角是60 ?,那么这个三角形一定是个锐角三角形。(??? )
⑤一个三角形中一定不可能有两个钝角。(?? )
×
√
×
×
√
125°
60°
1
2
根据下图求 ∠1 和∠2各是多少度?
∠2﹦180°- 125° = 55°
∠1﹦180°- 60°-55°=75 °
小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来的一个角,另一块有原来的两个角。他想重新买一块玻璃安上,小明非常聪明,只带了其中的一块到玻璃店去,就配到了和原来一模一样的玻璃了。你知道他带的是哪一块吗?
拓展训练
小结 拓展
知识的升华
你能根据自己的知识求出四边形和正六边形的内角和吗?
4个三角形:180°×4=720°
两个三角形:180°×2=360 °
一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度吗?
?
一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和是( )度。
180
拓展应用:
根据所学的知识,你算出下列图形的内角和吗?
总结:
通过今天的学习,大家有什么收获?
人教版四年下册
三角形的内角和
由三条线段围成的图形叫做三角形.
角
角
角
边
边
边
顶点
顶点
顶点
旧知回顾:
已知∠1=300, ∠2=800,求∠3的度数。
300
800
?
旧知回顾:
正方形和长方形的内角和是多少度?
900
900
900
900
900
900
900
900
旧知回顾:
你的三边之和。是比我长,但三个内角之和并不比我大
我不但三边之和比你长,而且三个内角之和也比你大!
你同意谁的说法呢?为什么?
创设情境:
1:什么是三角形的内角?
2:三角形有几个内角?
3:什么是三角形的内角和?
自主探究:
算一算,两块三角板的内角和分别是多少度呢?
30
45
45
60
90
90
三角板
大小、形状不同的三角形,它们的内角和一样吗?都是180?吗?
三角形按角分,可以分为哪几类?
猜一猜 想一想
大家一起认一认,分一分!
锐角三角形
钝角三角形
直角三角形
小组活动:
(1)小组分工。
(2)同学们能通过动手操作,想办法来验证自己的猜想吗? 请同学们先独立思考想一想,再在小组内把你的想法与同伴进行交流,然后选用一种方法进行验证。
(3)最后要求计算出三个角的和是多少?填在表格里。
∠1 ∠2 ∠3 内角和 发现规律
锐角三角形
直角三角形
钝角三角形
分小组汇报交流
量一量
小组活动一:
撕一撕
拼一拼
小组活动二:
3
2
3
1
平角:1800
三角形的内角和是1800。
2
1
折一折
拼一拼
小组活动三:
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
得出结论:
三角形的内角和是1800。
在一个三角形中,已知∠1=1400,∠3=250,求∠2的度数?
1800-1400-250
=400-250
=150
答:∠2的度数为150。
内角和1800
做一做
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
分层训练:
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
1800-700×2
=1800 -1400
=400
1800-700 -700
=1100 -700
=400
700
700
400
内角和1800
答:它的顶角是400。
1800÷3=60°
(1800-960) ÷2
=840÷2
=42°
①1800-900-400
=900-400
=50°
我的一个角是多少度?
我的一个底角是多少度?
我是一个直角三角形,我的另一个锐角是多少度?
②900-400=50°
三角形∠1=140°∠3=25°求∠2的度数。
180°-140°-25°=15°
180 °-(140° +25°)=15 °
140°
25°
?
75°
35°
?
75°
35°
180° -75 ° - 35°=70°
180° -(75 ° + 35°)=70°
?
已知等腰三角形的风筝,一个底角70°,顶角多少度?
180°-70°-70°=40°
180°-70°×2=40°
70°
70°
?
180°-90°-50°=40°
180° -(50°+90°)=40 °
一个直角三角形,一个锐角是50°,另一个锐角是几度?
50°
90°-50°=40°
?
选择
1.下面每组三个角,不可能在同一个三角内的是( )。
A.15° 78° 87°B.55° 120° 5°C.90° 18° 102°
2.把一个三角形纸片剪成两个小三角形,每个小三角形的内角和( )180度。
A.大于 B.小于 C.等于
C
C
判断下列说法对吗?
①钝角三角形的内角和大于锐角三角形的内角和。(??? )
②在直角三角形中,两个锐角的和等于90 ?。(??? )
③在钝角三角形中,两个锐角的和大于90 ?。(??? )
④三角形中有一个角是60 ?,那么这个三角形一定是个锐角三角形。(??? )
⑤一个三角形中一定不可能有两个钝角。(?? )
×
√
×
×
√
125°
60°
1
2
根据下图求 ∠1 和∠2各是多少度?
∠2﹦180°- 125° = 55°
∠1﹦180°- 60°-55°=75 °
小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来的一个角,另一块有原来的两个角。他想重新买一块玻璃安上,小明非常聪明,只带了其中的一块到玻璃店去,就配到了和原来一模一样的玻璃了。你知道他带的是哪一块吗?
拓展训练
小结 拓展
知识的升华
你能根据自己的知识求出四边形和正六边形的内角和吗?
4个三角形:180°×4=720°
两个三角形:180°×2=360 °
一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度吗?
?
一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和是( )度。
180
拓展应用:
根据所学的知识,你算出下列图形的内角和吗?
总结:
通过今天的学习,大家有什么收获?
