六年级下册数学课件圆柱表面积、体积能力提升题北师大版 (共20张)
文档属性
| 名称 | 六年级下册数学课件圆柱表面积、体积能力提升题北师大版 (共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 13:51:52 | ||
图片预览






文档简介
(共20张PPT)
六年级数学
圆柱表面积、体积提升题
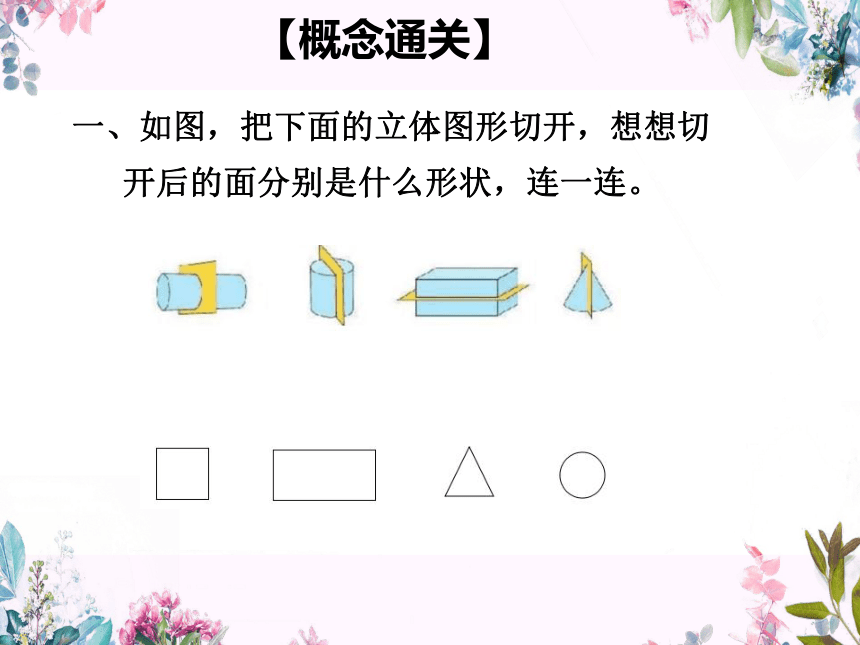
【概念通关】
一、如图,把下面的立体图形切开,想想切
开后的面分别是什么形状,连一连。
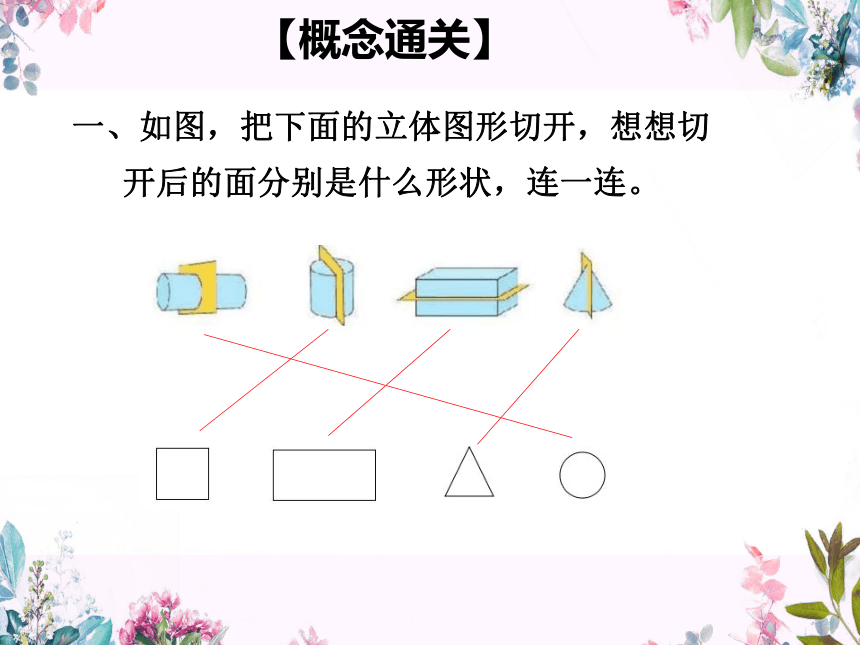
【概念通关】
一、如图,把下面的立体图形切开,想想切
开后的面分别是什么形状,连一连。
【典型例题】
例1、把一个底面半径是2分米,长是9分米的圆柱
形木头锯成长短不同的三小段圆柱形木头,表面
积之和比原来增加了多少平方分米?
【典型例题】
例1、把一个底面半径是2分米,长是9分米的圆柱
形木头锯成长短不同的三小段圆柱形木头,表面
积之和比原来增加了多少平方分米?
段数 - 1 = 切的次数
切1次增加2个面
3 - 1 = 2(次)
2 × 2 = 4(面)
3.14×2?×4=50.24(cm?)
答:表面积之和比原来增加了50.24平方分米。
横切圆柱1次增加2个底面
【巩固加油站】
1、把两个完全相同的、底面直径是4厘米的圆柱形
钢材,焊接成一个大的圆柱形钢材,焊接后的表
面积比原来表面积之和减少了多少平方厘米?
2个底面积相等的圆柱拼接起来,减少了2个底面
半径:4÷2=2(厘米)
2个底面积:3.14×2?×2=25.12(厘米)
答:表面积之和减少了25.12平方厘米。
【巩固加油站】
2、把一个高9分米的大圆柱切成2个小圆柱,表面
积增加了12.56平方分米。原来大圆柱的体积是
多少立方分米?
一个底面积:12.56÷2 = 6.28(dm?)
体积:6.28×9 = 56.52(dm?)
答:原来大圆柱的体积是56.52立方分米。
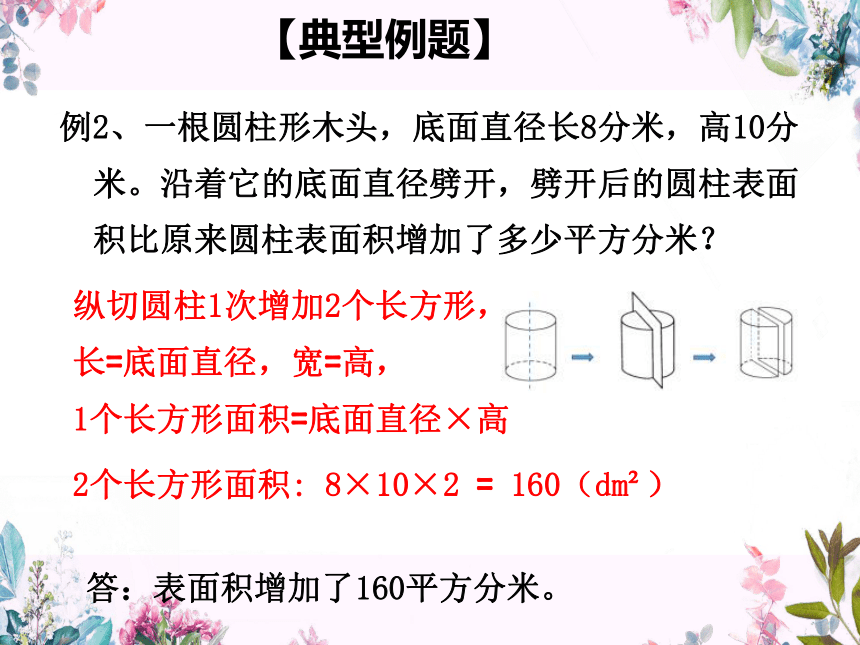
【典型例题】
例2、一根圆柱形木头,底面直径长8分米,高10分
米。沿着它的底面直径劈开,劈开后的圆柱表面
积比原来圆柱表面积增加了多少平方分米?
2个长方形面积: 8×10×2 = 160(dm?)
答:表面积增加了160平方分米。
1个长方形面积=底面直径×高
纵切圆柱1次增加2个长方形,长=底面直径,宽=高,
【巩固加油站】
3、一根长8分米的圆柱形木材,沿着它的直径竖着
切成两半,表面积增加了16平方分米。这根圆柱
形木材的体积是多少立方分米?
1个长方形面积:16÷2 = 8(dm?)
底面直径:8÷8 = 1(dm)
半径:1÷2 = 0.5(dm)
体积:3.14×0.5?×8= 6.28(dm?)
答:这根圆柱形木材的体积是6.28立方分米。
【巩固加油站】
4、两个完全一样的半圆柱,底面半径是3厘米,高
是9厘米,把它们合并成一个圆柱,它们的表面
积之和减少多少平方厘米?
直径:3×2 = 6(厘米)
6×9×2 = 108(厘米?)
【典型例题】
例3、一个圆柱,底面周长是6.28分米,高增加了2
分米,圆柱表面积增加了多少平方分米?
圆柱的高增加,增加了一个侧面,
增加的面积=底面周长×增加的高
6.28×2=12.56(dm?)
答:圆柱表面积增加了12.56平方分米。
【巩固加油站】
4、一根圆柱形木料底面半径2厘米,把它截下一段
长3cm的小圆柱后,剩下的表面积比原来的表面
积减少多少平方厘米?
3.14×2×2×3=37.68(cm?)
答:圆柱表面积减少了37.68平方厘米。
【典型例题】
例4、一根长方体木料,底面边长为4分米的正方形,
高是12分米,把它削成一个最大的圆柱。这个圆
柱的体积是多少立方分米?
半径:4÷2 = 2(dm)
体积:3.14×2?×12 = 150.72(dm?)
答:这个圆柱的体积是150.72立方分米。
【巩固加油站】
5、一个正方体棱长是6分米,把它削成一个最大的
圆柱。这个圆柱的体积是多少立方分米?
半径:6÷2 = 3(dm)
体积:3.14×3?×6 = 169.56(dm?)
答:这个圆柱的体积是169.56立方分米。
【典型例题】
例5、把一个底面直径是20厘米、高是12厘米的圆柱
体木料,削成一个最大的圆锥体。圆锥的体积是
多少立方厘米?削掉木料的体积是多少立方厘米?
把圆柱削成最大圆锥,圆柱与圆锥等底等高。
半径:20÷10=2(厘米)
圆锥体积:3.14×2?×12× =1256(厘米?)
削掉体积:1256×2 = 2512(厘米?)
答:
【典型例题】
例6、如图,求出小铁块的体积。
浸入水中物体的体积 = 涨高水的体积
半径:10÷2=5(cm)
体积:3.14×5?×2=157(cm?)
涨水的高度:7-5=2(cm)
【巩固加油站】
6、一个底面直径是4分米的圆柱形容器中装有水,
当把一块矿石浸没在水中时,水面高度升高了到
3厘米。这块矿石的体积是多少立方厘米?
4÷2=2(dm)=20(cm)
3.14×20?×3=3768(cm?)
答:这块矿石的体积是3768立方厘米。
【典型例题】
例7、把一个底面半径是6厘米,高是10厘米的圆锥形
容器灌满水,然后把水倒入一个底面半径是5厘米
的圆柱形容器里,求圆柱形容器内水面的高度?
倒水问题:水不溢出,水的体积不变。
水的体积:3.14×6?×10× =376.8(cm?)
高:376.8÷(3.14×5?)=4.8(cm)
答:圆柱形容器内水面的高度是4.8厘米。
【巩固加油站】
7、一个圆锥形的稻谷堆,?底面半径是3米,高1.5
米,把这堆稻谷装进一个圆柱形粮仓,正好装满。
这个粮仓里面的底面直径为4米,高是多少米?
粮食的体积:3.14×3?×1.5× = 14.13(米?)
高:14.13÷(3.14×2?)=1.125(米)
半径:4÷2 = 2(米)
答:高是1.125米。
我还会再回来的!!
六年级数学
圆柱表面积、体积提升题
【概念通关】
一、如图,把下面的立体图形切开,想想切
开后的面分别是什么形状,连一连。
【概念通关】
一、如图,把下面的立体图形切开,想想切
开后的面分别是什么形状,连一连。
【典型例题】
例1、把一个底面半径是2分米,长是9分米的圆柱
形木头锯成长短不同的三小段圆柱形木头,表面
积之和比原来增加了多少平方分米?
【典型例题】
例1、把一个底面半径是2分米,长是9分米的圆柱
形木头锯成长短不同的三小段圆柱形木头,表面
积之和比原来增加了多少平方分米?
段数 - 1 = 切的次数
切1次增加2个面
3 - 1 = 2(次)
2 × 2 = 4(面)
3.14×2?×4=50.24(cm?)
答:表面积之和比原来增加了50.24平方分米。
横切圆柱1次增加2个底面
【巩固加油站】
1、把两个完全相同的、底面直径是4厘米的圆柱形
钢材,焊接成一个大的圆柱形钢材,焊接后的表
面积比原来表面积之和减少了多少平方厘米?
2个底面积相等的圆柱拼接起来,减少了2个底面
半径:4÷2=2(厘米)
2个底面积:3.14×2?×2=25.12(厘米)
答:表面积之和减少了25.12平方厘米。
【巩固加油站】
2、把一个高9分米的大圆柱切成2个小圆柱,表面
积增加了12.56平方分米。原来大圆柱的体积是
多少立方分米?
一个底面积:12.56÷2 = 6.28(dm?)
体积:6.28×9 = 56.52(dm?)
答:原来大圆柱的体积是56.52立方分米。
【典型例题】
例2、一根圆柱形木头,底面直径长8分米,高10分
米。沿着它的底面直径劈开,劈开后的圆柱表面
积比原来圆柱表面积增加了多少平方分米?
2个长方形面积: 8×10×2 = 160(dm?)
答:表面积增加了160平方分米。
1个长方形面积=底面直径×高
纵切圆柱1次增加2个长方形,长=底面直径,宽=高,
【巩固加油站】
3、一根长8分米的圆柱形木材,沿着它的直径竖着
切成两半,表面积增加了16平方分米。这根圆柱
形木材的体积是多少立方分米?
1个长方形面积:16÷2 = 8(dm?)
底面直径:8÷8 = 1(dm)
半径:1÷2 = 0.5(dm)
体积:3.14×0.5?×8= 6.28(dm?)
答:这根圆柱形木材的体积是6.28立方分米。
【巩固加油站】
4、两个完全一样的半圆柱,底面半径是3厘米,高
是9厘米,把它们合并成一个圆柱,它们的表面
积之和减少多少平方厘米?
直径:3×2 = 6(厘米)
6×9×2 = 108(厘米?)
【典型例题】
例3、一个圆柱,底面周长是6.28分米,高增加了2
分米,圆柱表面积增加了多少平方分米?
圆柱的高增加,增加了一个侧面,
增加的面积=底面周长×增加的高
6.28×2=12.56(dm?)
答:圆柱表面积增加了12.56平方分米。
【巩固加油站】
4、一根圆柱形木料底面半径2厘米,把它截下一段
长3cm的小圆柱后,剩下的表面积比原来的表面
积减少多少平方厘米?
3.14×2×2×3=37.68(cm?)
答:圆柱表面积减少了37.68平方厘米。
【典型例题】
例4、一根长方体木料,底面边长为4分米的正方形,
高是12分米,把它削成一个最大的圆柱。这个圆
柱的体积是多少立方分米?
半径:4÷2 = 2(dm)
体积:3.14×2?×12 = 150.72(dm?)
答:这个圆柱的体积是150.72立方分米。
【巩固加油站】
5、一个正方体棱长是6分米,把它削成一个最大的
圆柱。这个圆柱的体积是多少立方分米?
半径:6÷2 = 3(dm)
体积:3.14×3?×6 = 169.56(dm?)
答:这个圆柱的体积是169.56立方分米。
【典型例题】
例5、把一个底面直径是20厘米、高是12厘米的圆柱
体木料,削成一个最大的圆锥体。圆锥的体积是
多少立方厘米?削掉木料的体积是多少立方厘米?
把圆柱削成最大圆锥,圆柱与圆锥等底等高。
半径:20÷10=2(厘米)
圆锥体积:3.14×2?×12× =1256(厘米?)
削掉体积:1256×2 = 2512(厘米?)
答:
【典型例题】
例6、如图,求出小铁块的体积。
浸入水中物体的体积 = 涨高水的体积
半径:10÷2=5(cm)
体积:3.14×5?×2=157(cm?)
涨水的高度:7-5=2(cm)
【巩固加油站】
6、一个底面直径是4分米的圆柱形容器中装有水,
当把一块矿石浸没在水中时,水面高度升高了到
3厘米。这块矿石的体积是多少立方厘米?
4÷2=2(dm)=20(cm)
3.14×20?×3=3768(cm?)
答:这块矿石的体积是3768立方厘米。
【典型例题】
例7、把一个底面半径是6厘米,高是10厘米的圆锥形
容器灌满水,然后把水倒入一个底面半径是5厘米
的圆柱形容器里,求圆柱形容器内水面的高度?
倒水问题:水不溢出,水的体积不变。
水的体积:3.14×6?×10× =376.8(cm?)
高:376.8÷(3.14×5?)=4.8(cm)
答:圆柱形容器内水面的高度是4.8厘米。
【巩固加油站】
7、一个圆锥形的稻谷堆,?底面半径是3米,高1.5
米,把这堆稻谷装进一个圆柱形粮仓,正好装满。
这个粮仓里面的底面直径为4米,高是多少米?
粮食的体积:3.14×3?×1.5× = 14.13(米?)
高:14.13÷(3.14×2?)=1.125(米)
半径:4÷2 = 2(米)
答:高是1.125米。
我还会再回来的!!
