北师大版八年级数学下册同步课件1.1.2等腰三角形(25张)
文档属性
| 名称 | 北师大版八年级数学下册同步课件1.1.2等腰三角形(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 383.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览



文档简介
课件25张PPT。第一节 等腰三角形(二)第一章 三角形的证明北师大版 八年级上册等腰三角形的性质:
(1)等腰三角形的两个底角相等. (等边对等角)
(2)等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)
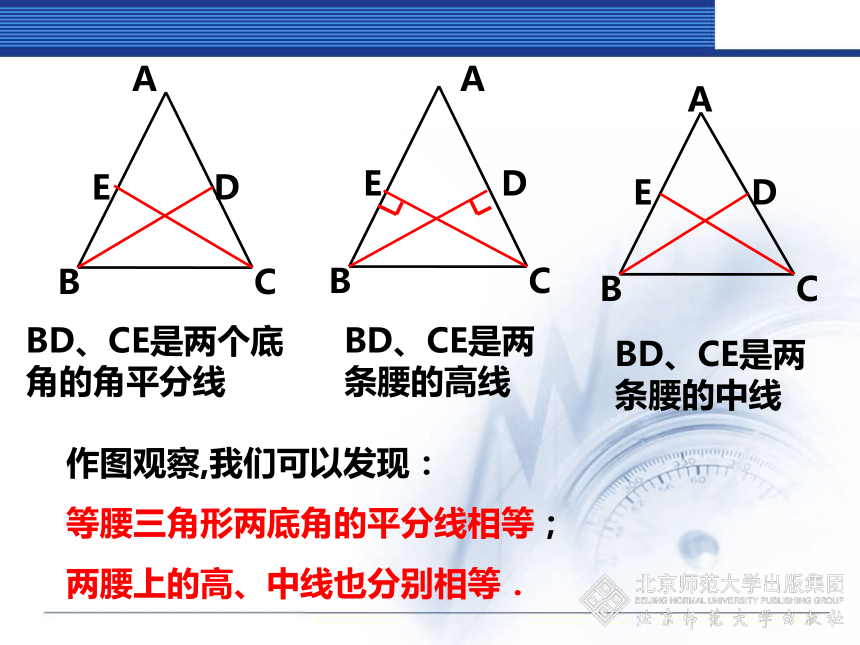
一、复习导入 在等腰三角形中作出一些线段—底角的角平分线、腰上的中线、腰上的高线等;
你能发现其中一些相等的线段吗?你能证明你的结论吗?二、探究新知BD、CE是两个底角的角平分线BD、CE是两条腰的高线BD、CE是两条腰的中线作图观察,我们可以发现:
等腰三角形两底角的平分线相等;
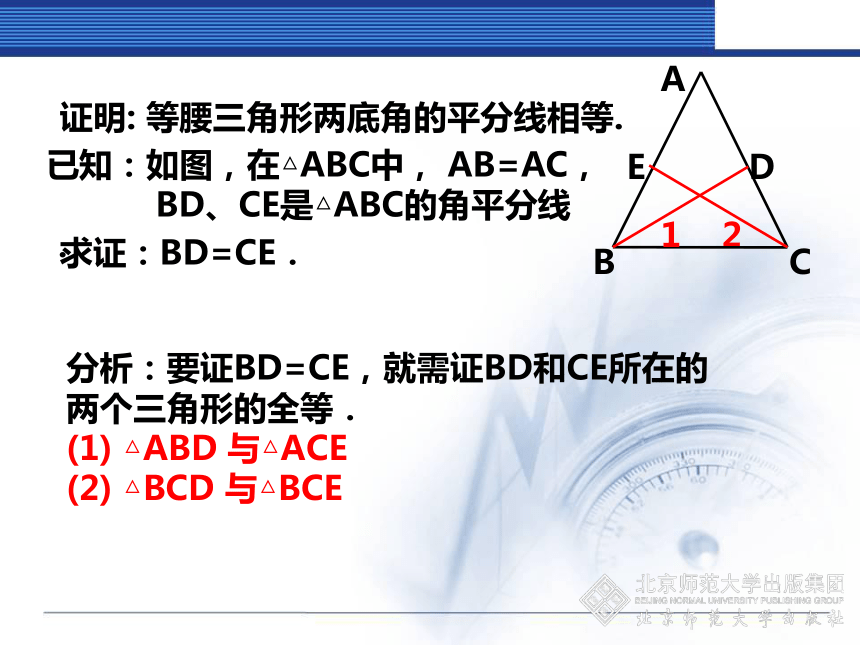
两腰上的高、中线也分别相等. 已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.
(1) △ABD 与△ACE
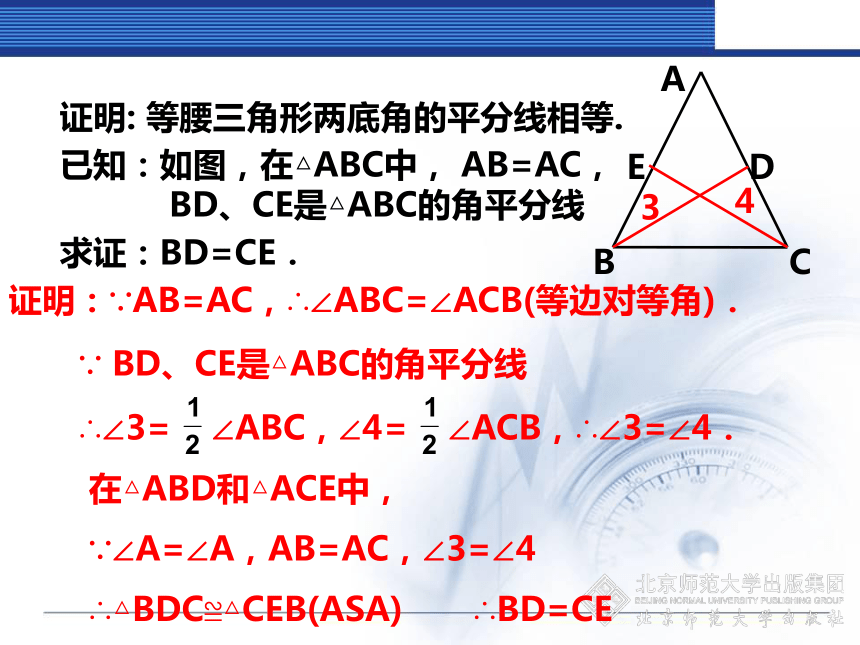
(2) △BCD 与△BCE已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵ BD、CE是△ABC的角平分线
∴∠1= ∠ABC,∠2= ∠ACB,∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2
∴△BDC≌△CEB(ASA) ∴BD=CE1已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵ BD、CE是△ABC的角平分线
∴∠3= ∠ABC,∠4= ∠ACB,∴∠3=∠4.
在△ABD和△ACE中,
∵∠A=∠A,AB=AC,∠3=∠4
∴△BDC≌△CEB(ASA) ∴BD=CE34已知:如图,在△ABC中, AB=AC,
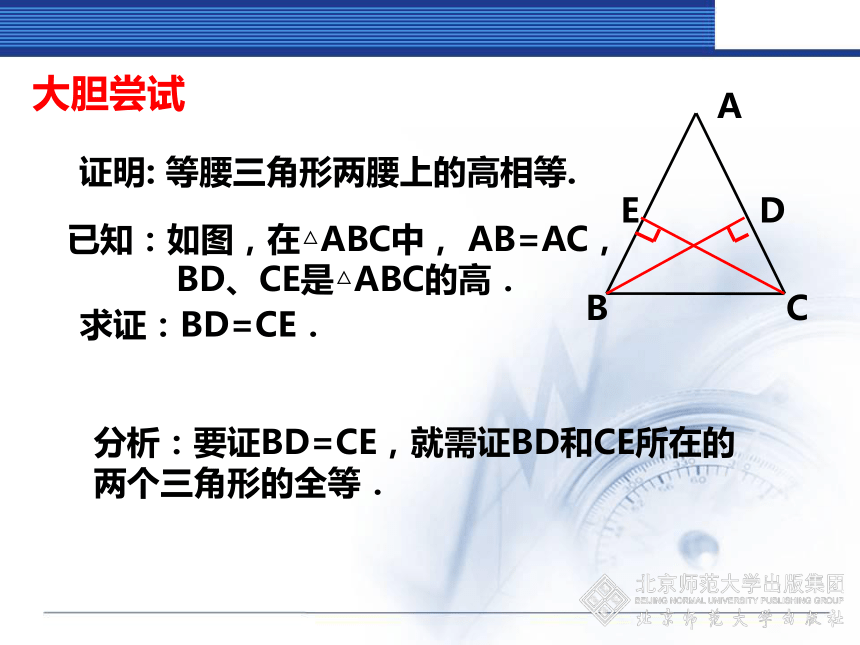
BD、CE是△ABC的高. 证明: 等腰三角形两腰上的高相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.大胆尝试已知:如图,在△ABC中, AB=AC,
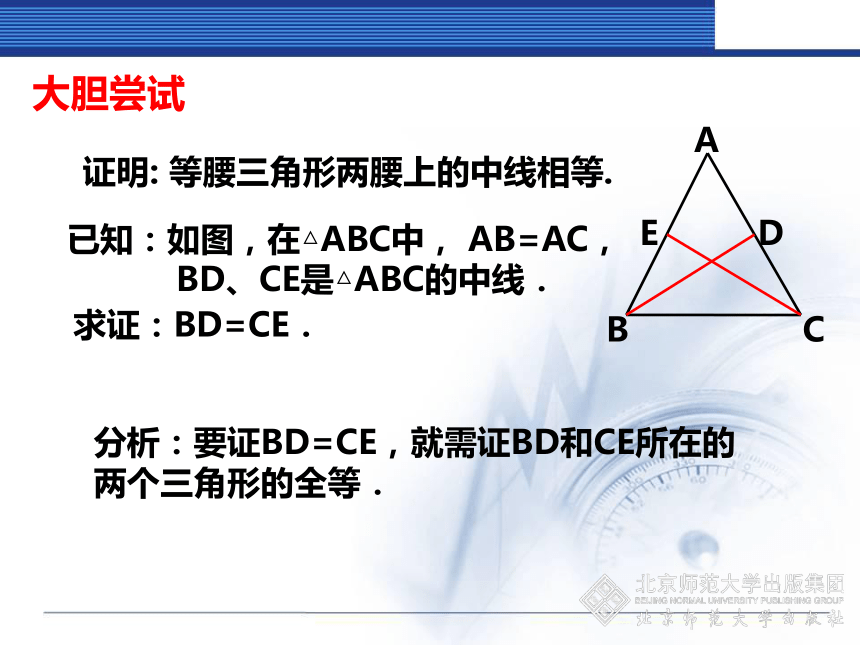
BD、CE是△ABC的中线.证明: 等腰三角形两腰上的中线相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.大胆尝试等腰三角形的性质
等腰三角形两底角的平分线相等;
两腰上的高、中线也分别相等. 思维拓展2思维拓展(1)在△ABC中,如果AB=AC,
∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE.
(2)在△ABC中,如果AB=AC,
AD= AC,AE= AB,那么BD=CE.归纳总结 简述为:
(1)在△ABC中,AB=AC,
如果∠ABD=∠ACE( ∠1=∠2 ),那么BD=CE.
(2)在△ABC中,AB=AC,如果AD=AE,那么BD=CE.归纳总结2三、知识深化等边三角形(特殊的等腰三角形)
定义:三边都相等的三角形叫等边三角形;
性质(特殊):
具有等腰三角形的一切性质
等边三角形三个内角都相等,并且每个内角都等于60°.
求证:等边三角形三个内角都相等,并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理,得∠C=∠A, ∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.四、巩固练习1.求等边三角形两条中线相交所成锐角的度数。
如图,BD、CE是等边三角△ABC的两条中线,
BD与CE相较于点O,求BOE的大小。
2.已知:如图,P、Q是△ABC的边BC上的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.四、巩固练习3.如图,在△ ABC中,AB=AC,点D为BC的中点,点E、F分别在AB和AC上,并且AE=AF。
求证:DE=DF。4.如图,已知△ ABC和△BDE都是等边三角形
求证:AE=CD
证明:∵ △ABC和△BDE都是等边三角形∴ AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD(SAS)∴ AE=CD四、巩固练习5.如图,已知△ABC是等边三角形,AE=CD,
(1)求证:∠CAD= ∠ABE;
(2)求∠BFD的度数; 1.等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等;
2.等边三角形的三个内角都相等,并且每个角都等于600。
3.等边三角形是特殊的等腰三角形,具有等腰三角形的一切性质。
4.本节课探索问题的方法:
—证需要证的线段所在的两个三角形的全等.
五、课堂小结六、布置作业1.完成课本习题1.2中第1、2、3、4、5、6题
2.拓展作业:
将不全等的两个等边三角形△ABC和△DEF任意摆放,请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的一条直线上有且只有三个顶点(重合的顶点算一个),并说明理由.ABCFE谢谢聆听!
(1)等腰三角形的两个底角相等. (等边对等角)
(2)等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)
一、复习导入 在等腰三角形中作出一些线段—底角的角平分线、腰上的中线、腰上的高线等;
你能发现其中一些相等的线段吗?你能证明你的结论吗?二、探究新知BD、CE是两个底角的角平分线BD、CE是两条腰的高线BD、CE是两条腰的中线作图观察,我们可以发现:
等腰三角形两底角的平分线相等;
两腰上的高、中线也分别相等. 已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.
(1) △ABD 与△ACE
(2) △BCD 与△BCE已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵ BD、CE是△ABC的角平分线
∴∠1= ∠ABC,∠2= ∠ACB,∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2
∴△BDC≌△CEB(ASA) ∴BD=CE1已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.证明: 等腰三角形两底角的平分线相等.求证:BD=CE.证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵ BD、CE是△ABC的角平分线
∴∠3= ∠ABC,∠4= ∠ACB,∴∠3=∠4.
在△ABD和△ACE中,
∵∠A=∠A,AB=AC,∠3=∠4
∴△BDC≌△CEB(ASA) ∴BD=CE34已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高. 证明: 等腰三角形两腰上的高相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.大胆尝试已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.证明: 等腰三角形两腰上的中线相等.求证:BD=CE.分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.大胆尝试等腰三角形的性质
等腰三角形两底角的平分线相等;
两腰上的高、中线也分别相等. 思维拓展2思维拓展(1)在△ABC中,如果AB=AC,
∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE.
(2)在△ABC中,如果AB=AC,
AD= AC,AE= AB,那么BD=CE.归纳总结 简述为:
(1)在△ABC中,AB=AC,
如果∠ABD=∠ACE( ∠1=∠2 ),那么BD=CE.
(2)在△ABC中,AB=AC,如果AD=AE,那么BD=CE.归纳总结2三、知识深化等边三角形(特殊的等腰三角形)
定义:三边都相等的三角形叫等边三角形;
性质(特殊):
具有等腰三角形的一切性质
等边三角形三个内角都相等,并且每个内角都等于60°.
求证:等边三角形三个内角都相等,并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理,得∠C=∠A, ∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.四、巩固练习1.求等边三角形两条中线相交所成锐角的度数。
如图,BD、CE是等边三角△ABC的两条中线,
BD与CE相较于点O,求BOE的大小。
2.已知:如图,P、Q是△ABC的边BC上的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.四、巩固练习3.如图,在△ ABC中,AB=AC,点D为BC的中点,点E、F分别在AB和AC上,并且AE=AF。
求证:DE=DF。4.如图,已知△ ABC和△BDE都是等边三角形
求证:AE=CD
证明:∵ △ABC和△BDE都是等边三角形∴ AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD(SAS)∴ AE=CD四、巩固练习5.如图,已知△ABC是等边三角形,AE=CD,
(1)求证:∠CAD= ∠ABE;
(2)求∠BFD的度数; 1.等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等;
2.等边三角形的三个内角都相等,并且每个角都等于600。
3.等边三角形是特殊的等腰三角形,具有等腰三角形的一切性质。
4.本节课探索问题的方法:
—证需要证的线段所在的两个三角形的全等.
五、课堂小结六、布置作业1.完成课本习题1.2中第1、2、3、4、5、6题
2.拓展作业:
将不全等的两个等边三角形△ABC和△DEF任意摆放,请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的一条直线上有且只有三个顶点(重合的顶点算一个),并说明理由.ABCFE谢谢聆听!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
