北师大版八年级数学下册同步课件1.1.1等腰三角形(21张)
文档属性
| 名称 | 北师大版八年级数学下册同步课件1.1.1等腰三角形(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 513.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览





文档简介
课件21张PPT。第一节 等腰三角形(一)第一章 三角形的证明北师大版 八年级上册基本事实:
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边及其夹角对应相等的两个三角形全等; (SAS)
4.两角及其夹边对应相等的两个三角形全等; (ASA)
5.三边对应相等的两个三角形全等; (SSS)一、复习导入你能证明下面的推论吗?
推论:两角及其中一角的对边对应相等的两个三角形全等.(AAS)证明文字命题的步骤:
(1)画图;
(2)写“已知”、“求证”;
(3)证明命题.(根据公理或定理证明)
证明:两角及其中一角的对边对应相等的两个三角形全等.已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知) ∴∠C=∠F(等量代换)
∵ 在△ABC和△DEF中,∠B=∠E , BC=EF ,∠C=∠F
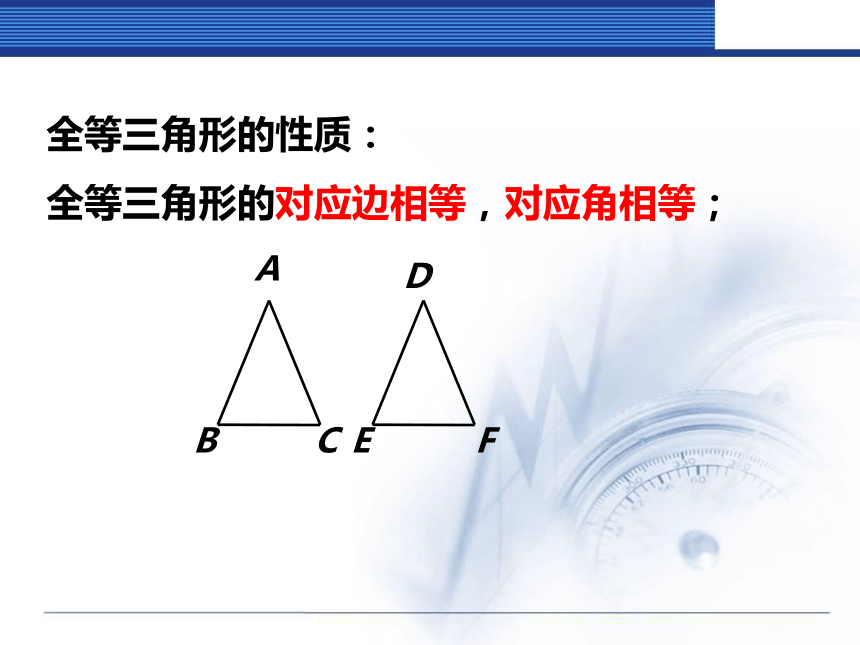
∴△ABC≌△DEF(ASA)全等三角形的性质:
全等三角形的对应边相等,对应角相等;二、探究新知等腰三角形
1.定义:有两条边相等的的三角形叫等腰三角形
2.还记得我们探索过的等腰三角形的性质吗?
3.你能利用已有的公理和定理证明这些结论吗?(1)等腰三角形的两底角相等;
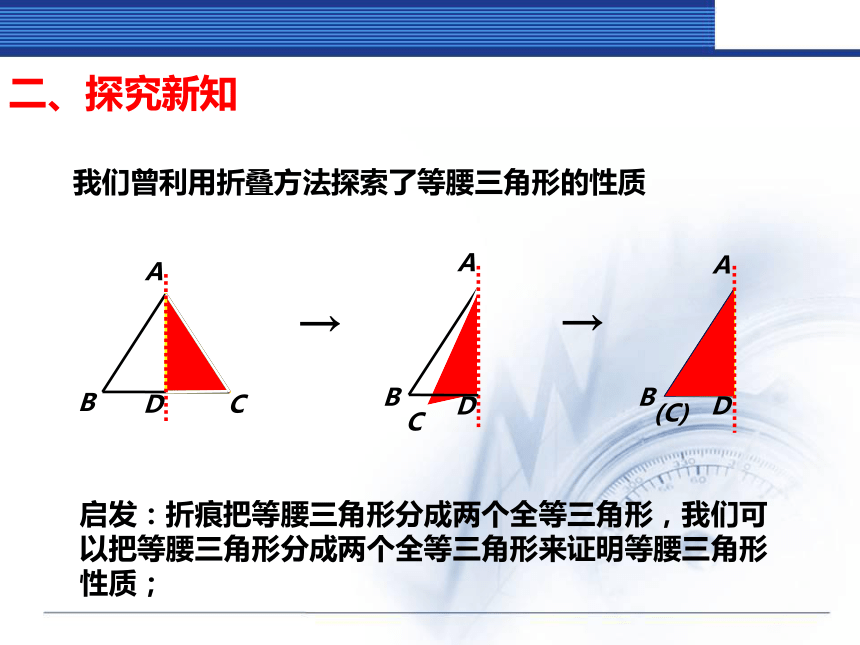
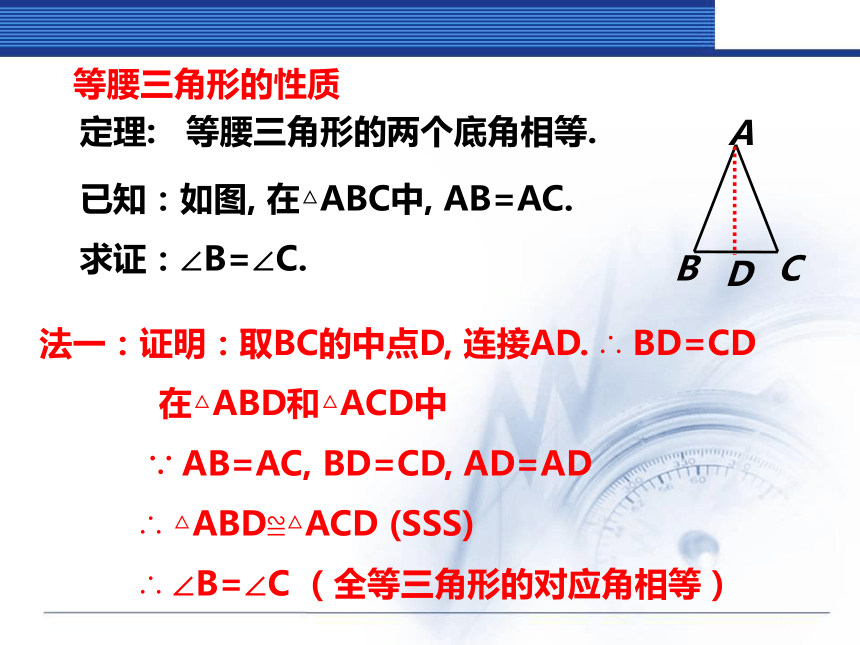
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”二、探究新知我们曾利用折叠方法探索了等腰三角形的性质启发:折痕把等腰三角形分成两个全等三角形,我们可以把等腰三角形分成两个全等三角形来证明等腰三角形性质;定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法一:证明:取BC的中点D, 连接AD. ∴ BD=CD
在△ABD和△ACD中
∵ AB=AC, BD=CD, AD=AD
∴ △ABD≌△ACD (SSS)
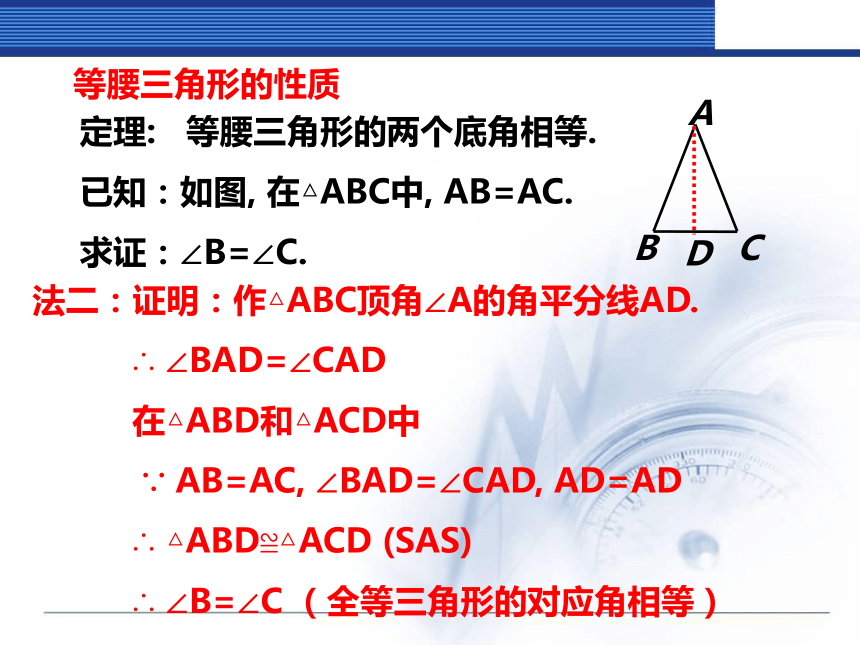
∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法二:证明:作△ABC顶角∠A的角平分线AD.
∴ ∠BAD=∠CAD
在△ABD和△ACD中
∵ AB=AC, ∠BAD=∠CAD, AD=AD
∴ △ABD≌△ACD (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法三:证明:过点A作BC的垂线交BC于点D,
∴ ∠ADB= ∠ADC=90°
在Rt△ABD和Rt △ACD中,由勾股定理,得
∴ BD 2 =AB 2 -AD 2,CD 2 =AC 2 -AD 2,
∵ AC=AB,AD=AD, ∴ BD=CD
∴ BD=CD , AD=AD, ∴ ∠ADB= ∠ADC=90°
∴ △ABD≌△ACD (SAS) ∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质点拨:在上面的图形中,线段AD还具有怎样的性质?为什么?由此你能得到什么结论?(1)定理: 等腰三角形的两个底角相等. 等腰三角形的性质AB=AC ∠B=∠C定理简述为:等边对等角 (2)推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)三、巩固练习1.已知等腰三形的一个顶角为36°,则它的两个底角分别 为 。
3.已知等腰三角形的一个外角为70°,则这个三角形的
三个内角分别为 。72° 、72°70° 、70° 或 40°、100°110° 、35° 、35°2.已知等腰三角形的一个角为40°,则其它两个角分别为 。3.等腰三角形一个角为110°,则它的另外两个角分别
为___ ___ _.35 °,35 °三、巩固练习5.等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;10 cm6.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;10 cm 或 11 cm7.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。19 cm数学思想——分类讨论
(1) 给出一条角的大小,要分顶角和底角的情景讨论,还要注意底角小于90°;
(2) 给出一条边的长短,要分腰和底边的情况讨论,同时还要注意三边能组成三角形;2.如图,厂房屋顶钢架外框△ABC,AB=AC,立柱AD⊥BC.
已知∠B=30°, BC=6m,
∠BAC= , BD= . 120°3m1.在 △ABC 中,AB = AC.
(1)若 ∠ A = 40°,则 ∠ C 等于 度.
(2)若 ∠ B = 72°,则 ∠ A 等于 度.70363.将下面证明中每一步的理由写在括号内:已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )已知已知公共边SSS全等三角形的对应角相等4.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD,
(1)求证: △ABD是等腰三角形;
(2)求∠BAD的度数.四、课堂小结小结:通过本节课的学习,谈谈收获及疑惑1、本节主要学习了等腰三角形的两个性质等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 顶角平分线、底边上的中线、底边上的高互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、数学思想:
分类讨论—注意等腰三角形的特殊性
(1) 给出一条角的大小,要分顶角和底角的情景讨论,还要注意底角小于90°;
(2) 给出一条边的长短,要分腰和底边的情况讨论,同时还要注意三边能组成三角形;四、课堂小结五、布置作业完成课本习题1.1中第2、3、4、5、6题
拓展作业:在△ABC,AB=AC,BD⊥AC,探索∠DBC与∠A之间关系?教师寄语:
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯谢谢聆听!
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边及其夹角对应相等的两个三角形全等; (SAS)
4.两角及其夹边对应相等的两个三角形全等; (ASA)
5.三边对应相等的两个三角形全等; (SSS)一、复习导入你能证明下面的推论吗?
推论:两角及其中一角的对边对应相等的两个三角形全等.(AAS)证明文字命题的步骤:
(1)画图;
(2)写“已知”、“求证”;
(3)证明命题.(根据公理或定理证明)
证明:两角及其中一角的对边对应相等的两个三角形全等.已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知) ∴∠C=∠F(等量代换)
∵ 在△ABC和△DEF中,∠B=∠E , BC=EF ,∠C=∠F
∴△ABC≌△DEF(ASA)全等三角形的性质:
全等三角形的对应边相等,对应角相等;二、探究新知等腰三角形
1.定义:有两条边相等的的三角形叫等腰三角形
2.还记得我们探索过的等腰三角形的性质吗?
3.你能利用已有的公理和定理证明这些结论吗?(1)等腰三角形的两底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”二、探究新知我们曾利用折叠方法探索了等腰三角形的性质启发:折痕把等腰三角形分成两个全等三角形,我们可以把等腰三角形分成两个全等三角形来证明等腰三角形性质;定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法一:证明:取BC的中点D, 连接AD. ∴ BD=CD
在△ABD和△ACD中
∵ AB=AC, BD=CD, AD=AD
∴ △ABD≌△ACD (SSS)
∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法二:证明:作△ABC顶角∠A的角平分线AD.
∴ ∠BAD=∠CAD
在△ABD和△ACD中
∵ AB=AC, ∠BAD=∠CAD, AD=AD
∴ △ABD≌△ACD (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质定理: 等腰三角形的两个底角相等. 已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.法三:证明:过点A作BC的垂线交BC于点D,
∴ ∠ADB= ∠ADC=90°
在Rt△ABD和Rt △ACD中,由勾股定理,得
∴ BD 2 =AB 2 -AD 2,CD 2 =AC 2 -AD 2,
∵ AC=AB,AD=AD, ∴ BD=CD
∴ BD=CD , AD=AD, ∴ ∠ADB= ∠ADC=90°
∴ △ABD≌△ACD (SAS) ∴ ∠B=∠C (全等三角形的对应角相等)等腰三角形的性质点拨:在上面的图形中,线段AD还具有怎样的性质?为什么?由此你能得到什么结论?(1)定理: 等腰三角形的两个底角相等. 等腰三角形的性质AB=AC ∠B=∠C定理简述为:等边对等角 (2)推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)三、巩固练习1.已知等腰三形的一个顶角为36°,则它的两个底角分别 为 。
3.已知等腰三角形的一个外角为70°,则这个三角形的
三个内角分别为 。72° 、72°70° 、70° 或 40°、100°110° 、35° 、35°2.已知等腰三角形的一个角为40°,则其它两个角分别为 。3.等腰三角形一个角为110°,则它的另外两个角分别
为___ ___ _.35 °,35 °三、巩固练习5.等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;10 cm6.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;10 cm 或 11 cm7.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。19 cm数学思想——分类讨论
(1) 给出一条角的大小,要分顶角和底角的情景讨论,还要注意底角小于90°;
(2) 给出一条边的长短,要分腰和底边的情况讨论,同时还要注意三边能组成三角形;2.如图,厂房屋顶钢架外框△ABC,AB=AC,立柱AD⊥BC.
已知∠B=30°, BC=6m,
∠BAC= , BD= . 120°3m1.在 △ABC 中,AB = AC.
(1)若 ∠ A = 40°,则 ∠ C 等于 度.
(2)若 ∠ B = 72°,则 ∠ A 等于 度.70363.将下面证明中每一步的理由写在括号内:已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )已知已知公共边SSS全等三角形的对应角相等4.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD,
(1)求证: △ABD是等腰三角形;
(2)求∠BAD的度数.四、课堂小结小结:通过本节课的学习,谈谈收获及疑惑1、本节主要学习了等腰三角形的两个性质等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 顶角平分线、底边上的中线、底边上的高互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、数学思想:
分类讨论—注意等腰三角形的特殊性
(1) 给出一条角的大小,要分顶角和底角的情景讨论,还要注意底角小于90°;
(2) 给出一条边的长短,要分腰和底边的情况讨论,同时还要注意三边能组成三角形;四、课堂小结五、布置作业完成课本习题1.1中第2、3、4、5、6题
拓展作业:在△ABC,AB=AC,BD⊥AC,探索∠DBC与∠A之间关系?教师寄语:
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯谢谢聆听!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
