人教A版高中数学必修四:1.2.3三角函数线 课件(共19张PPT)
文档属性
| 名称 | 人教A版高中数学必修四:1.2.3三角函数线 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 866.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
1.2.1任意角的三角函数------ 三角函数线
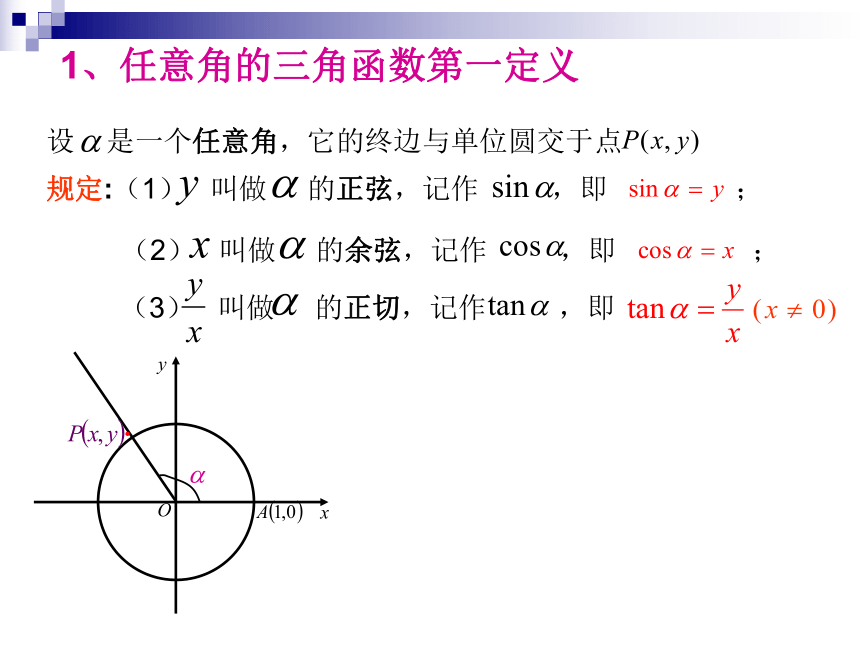
1、任意角的三角函数第一定义
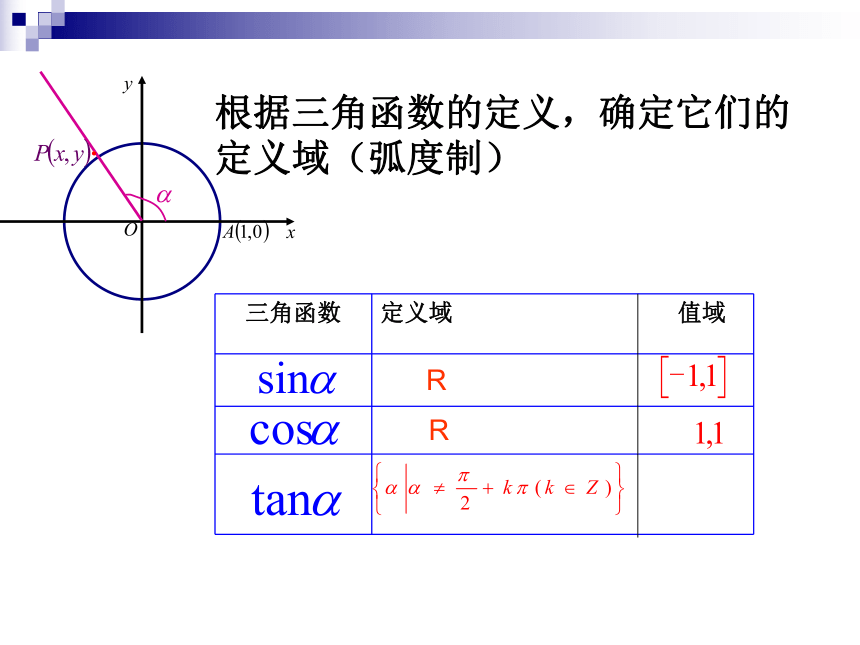
根据三角函数的定义,确定它们的定义域(弧度制)
R
R
三角函数 定义域 值域
2、任意角的三角函数第二定义:
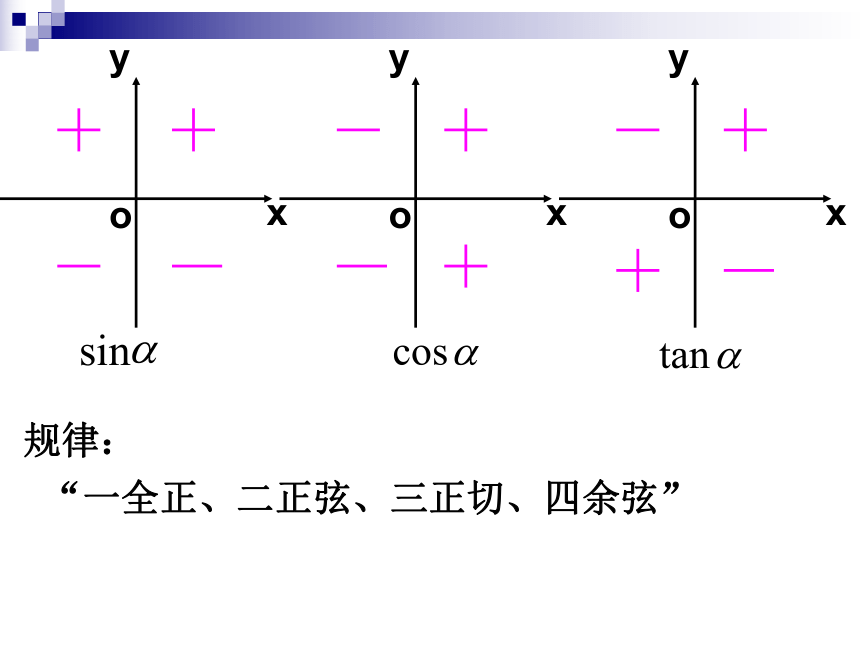
规律:
“一全正、二正弦、三正切、四余弦”
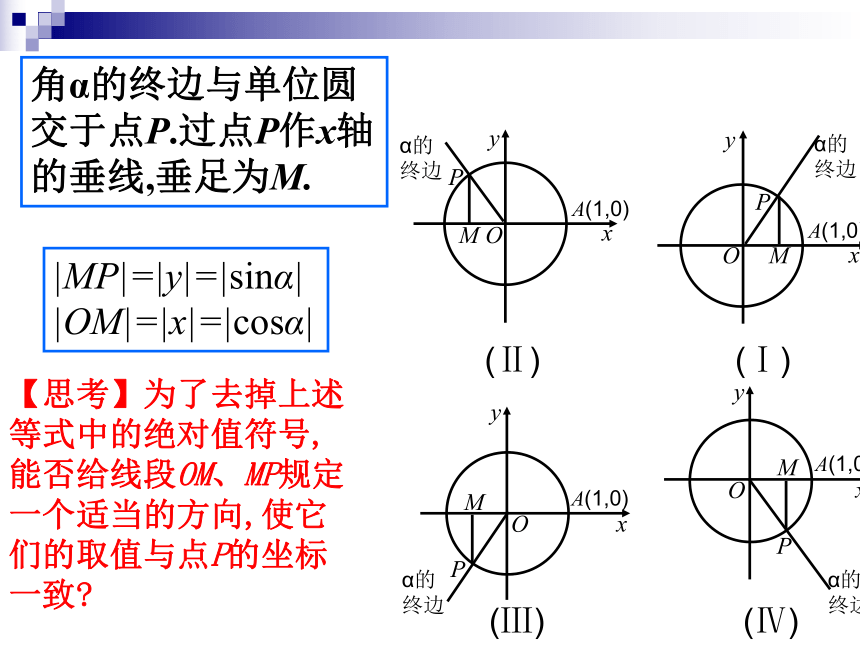
角α的终边与单位圆交于点P.过点P作x轴的垂线,垂足为M.
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
【思考】为了去掉上述等式中的绝对值符号,能否给线段OM、MP规定一个适当的方向,使它们的取值与点P的坐标一致?
【定义】有向线段
* 带有方向的线段叫有向线段.
*有向线段的大小称为它的数量.
在坐标系中,规定:
有向线段的方向与坐标系的方向相同.即同向时,数量为正;反向时,数量为负.
当角α的终边不在坐标轴上时,以M为始点、P为终点,
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
MP=y=sinα
有向线段MP叫角α的正弦线
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
OM=x=cosα
有向线段OM叫角α的余弦线
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.以A为始点、T为终点,
有向线段AT叫角α的正切线
这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线
---------任意角的三角函数第三定义
sinα =MP
cosα=OM
当角α的终边与x轴重合时,正弦线、正切线,分别变成一个点,此时角α的正弦值和正切值都为0;
当角α的终边与y轴重合时,余 弦线变成一个点,正切线不存 在,此时角α的正切值不存在.
sinα =MP=0
cosα=OM=1或-1
sinα =MP=1或-1
cosα=OM=0
例1 画出角 的三角函数线
P
M
T
例2 在单位圆中作出符合下列条件的角的终边:
例3.利用单位圆中的三角函数线,确定下列各角及取值范围:
sinα=cosα;
(2)sinα(3)tanα<1;
P
P
M
M
利用三角函数线求满足sinα= 角的集合
利用三角函数线求满足 角的集合
对于不等式
(其中α为锐角),你能用数形结合思想证明吗?
1.2.1任意角的三角函数------ 三角函数线
1、任意角的三角函数第一定义
根据三角函数的定义,确定它们的定义域(弧度制)
R
R
三角函数 定义域 值域
2、任意角的三角函数第二定义:
规律:
“一全正、二正弦、三正切、四余弦”
角α的终边与单位圆交于点P.过点P作x轴的垂线,垂足为M.
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
【思考】为了去掉上述等式中的绝对值符号,能否给线段OM、MP规定一个适当的方向,使它们的取值与点P的坐标一致?
【定义】有向线段
* 带有方向的线段叫有向线段.
*有向线段的大小称为它的数量.
在坐标系中,规定:
有向线段的方向与坐标系的方向相同.即同向时,数量为正;反向时,数量为负.
当角α的终边不在坐标轴上时,以M为始点、P为终点,
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
MP=y=sinα
有向线段MP叫角α的正弦线
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
OM=x=cosα
有向线段OM叫角α的余弦线
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.以A为始点、T为终点,
有向线段AT叫角α的正切线
这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线
---------任意角的三角函数第三定义
sinα =MP
cosα=OM
当角α的终边与x轴重合时,正弦线、正切线,分别变成一个点,此时角α的正弦值和正切值都为0;
当角α的终边与y轴重合时,余 弦线变成一个点,正切线不存 在,此时角α的正切值不存在.
sinα =MP=0
cosα=OM=1或-1
sinα =MP=1或-1
cosα=OM=0
例1 画出角 的三角函数线
P
M
T
例2 在单位圆中作出符合下列条件的角的终边:
例3.利用单位圆中的三角函数线,确定下列各角及取值范围:
sinα=cosα;
(2)sinα
P
P
M
M
利用三角函数线求满足sinα= 角的集合
利用三角函数线求满足 角的集合
对于不等式
(其中α为锐角),你能用数形结合思想证明吗?
