人教版九年级数学下册27.2.2:相似三角形的性质 课件 (共26张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.2:相似三角形的性质 课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 665.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 13:25:55 | ||
图片预览







文档简介
(共26张PPT)
27.2 相似三角形
27.2.2 相似三角形的性质
人教版数学九年级下册
甘肃省永昌县第六中学教师 勾延天
相似三角形的判定方法有哪些?
1、(简称:平行法)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
2、(简称:三边法):三边成比例的两个三角形相似.
3、(简称:两边夹角法):两边成比例且夹角相等的两个三 角形相似.
4、(简称:两角法):两角分别相等的两个三角形相似.√
复习回顾
5、(简称:斜边直角边法):斜边和一条直角边成比例的两个直角三角形相似。
根据条件,灵活选用
1.什么叫做相似三角形的相似比?
相似三角形对应边的比叫做相似比。
复习回顾
由相似三角形的定义可知:
相似三角形的性质1 相似三角形的对应角相等,对应边成比例。
符号语言 如果△ABC∽△A'B'C',相似比为k,那么
,∠A=∠A',∠B=∠B',∠C=∠C'.
2.你知道相似三角形都有那些性质?
相似三角形的性质和判定之间有什么联系?
相似三角形的判定:研究符合什么条件,两个三角形相似?
相似三角形的性质:研究两个三角形相似,可以得出什么结论?
思考
三角形中有各种各样的几何量,除边、角之外,还有高、中线、角平分线的长度以及周长与面积等,如果两个三角形相似,那么这些几何量之间有什么关系呢?这就是我们这节课要探究的问题.
导入新课
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
思考
A′
C′
B′
A
C
B
D
D′
A′
C′
B′
A
C
B
D
D′
A′
C′
B′
A
C
B
D
D′
A
C
B
A′
B′
C′
∽
(1)
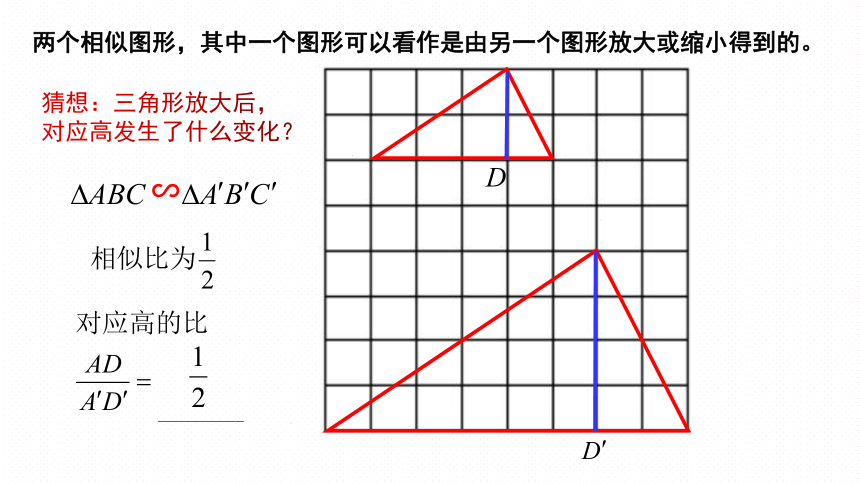
两个相似图形,其中一个图形可以看作是由另一个图形放大或缩小得到的。
猜想:三角形放大后,对应高发生了什么变化?
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应高AD和A'D'.
求证:
A′
C′
B′
A
C
B
D
D′
探究一
相似三角形对应高的比等于相似比
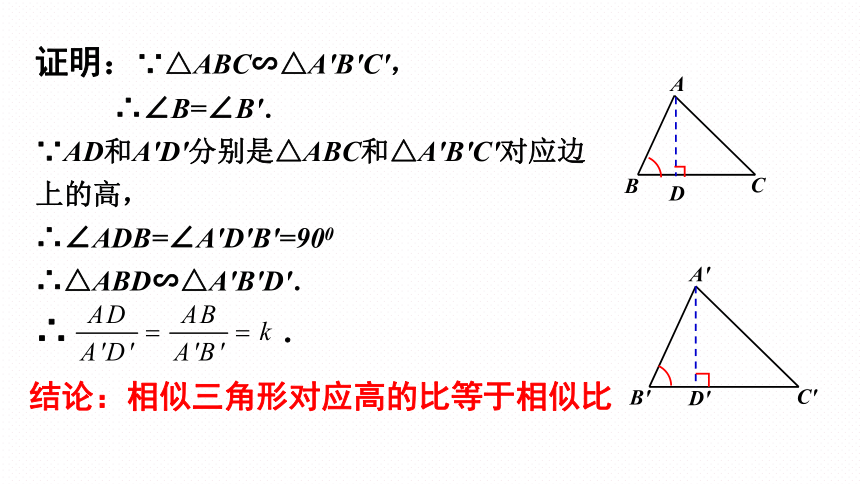
证明:∵△ABC∽△A'B'C',
∴∠B=∠B'.
∵AD和A'D'分别是△ABC和△A'B'C'对应边上的高,
∴∠ADB=∠A'D'B'=900
∴△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
结论:相似三角形对应高的比等于相似比
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应中线AD和A'D'.
求证:
A′
C′
B′
A
C
B
D
D′
探究二
相似三角形对应中线的比等于相似比
证明:∵△ABC∽△A'B'C',
∴∠B=∠B',
∴在△ABD与△A'B'D'中,
△ABD∽△A'B'D'.
∴ .
A
C
B
D
A′
C′
B′
D′
∵AD和A'D'分别是△ABC和△A'B'C'对应边上的中线,
结论:相似三角形对应中线的比等于相似比
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应角平分线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
探究三
相似三角形对应角平分线的比等于相似比
求证:
∴∠BAD= ∠BAC,
∴在△ABD与△A'B'D'中,
△ABD∽△A'B'D'.
∴
证明:∵△ABC∽△A'B'C',
∴∠B=∠B',∠BAC=∠B'A'C'.
∵AD和A'D'分别是∠BAC和∠B'A'C'的平分线,
A′
C′
B′
A
C
B
D′
D
结论:相似三角形对应角平分线的比等于相似比
null
新知归纳
这样我们得到
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有
相似三角形对应线段的比等于相似比.
null
新知归纳
几何语言
∵△ABC∽△AB'C',
AD和A'D'分别是它们的高.
D
D′
∴
相似三角形对应线段的比等于相似比
null
解:设△ABC和△A'B'C'的相似比为k,则
∴AB= kA′B′,BC= kB′C′,AC= kA′C′,
如果△ABC∽△A'B'C',相似比为k,那么△ABC与△A'B'C'的周长比是多少?
结论:相似三角形周长的比等于相似比.
探究四 相似三角形的周长比等于相似比
如图,△ABC∽△A′B′C′,相似比为k,△ABC与△A′B′C′的面积比是多少?
解:
结论:相似三角形面积的比等于相似比的平方.
A′
C′
B′
A
C
B
D
D′
探究五
相似三角形面积的比等于相似比的平方.
(1)已知ΔABC与ΔA'B'C' 的相似比为2:3,
则周长比为 ,对应边上中线之比为 ,
面积之比为 。
(2)已知ΔABC∽ΔA'B'C',且面积之比为9:4,
则周长之比为 ,相似比为 ,
对应边上的高线之比 。
2:3
4:9
3:2
3: 2
3:2
2:3
运用新知
1.判断题(正确的画“√”,错误的画“Χ”)
(1)一个三角形各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍;( )
(2)一个三角形各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.( )
√
Χ
《教材》P39 练习:
解:∵ △ABC ∽△DEF,
D
E
F
H
例1 已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG= 4.8 cm. 求 EH 的长.
∴ (相似三角形对应角平分线的比等于相似比),
∴ ,解得 EH = 3.2.
A
G
B
C
典例精析
∴ EH 的长为 3.2 cm.
null
相似三角形的面积比等于相似比的平方
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
例2 如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
挑战自我
如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN的边长为xcm。
∵PN∥BC,∴△APN∽ △ABC
∴
AE
AD
=
PN
BC
即
得 x=48cm。
答:正方形零件的边长为48cm。
80–x
80
=
x
120
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
课堂小结
相似三角形的性质有哪些?
布置作业
课堂作业
课本第58页第11题
同学们,再见!
27.2 相似三角形
27.2.2 相似三角形的性质
人教版数学九年级下册
甘肃省永昌县第六中学教师 勾延天
相似三角形的判定方法有哪些?
1、(简称:平行法)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
2、(简称:三边法):三边成比例的两个三角形相似.
3、(简称:两边夹角法):两边成比例且夹角相等的两个三 角形相似.
4、(简称:两角法):两角分别相等的两个三角形相似.√
复习回顾
5、(简称:斜边直角边法):斜边和一条直角边成比例的两个直角三角形相似。
根据条件,灵活选用
1.什么叫做相似三角形的相似比?
相似三角形对应边的比叫做相似比。
复习回顾
由相似三角形的定义可知:
相似三角形的性质1 相似三角形的对应角相等,对应边成比例。
符号语言 如果△ABC∽△A'B'C',相似比为k,那么
,∠A=∠A',∠B=∠B',∠C=∠C'.
2.你知道相似三角形都有那些性质?
相似三角形的性质和判定之间有什么联系?
相似三角形的判定:研究符合什么条件,两个三角形相似?
相似三角形的性质:研究两个三角形相似,可以得出什么结论?
思考
三角形中有各种各样的几何量,除边、角之外,还有高、中线、角平分线的长度以及周长与面积等,如果两个三角形相似,那么这些几何量之间有什么关系呢?这就是我们这节课要探究的问题.
导入新课
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
思考
A′
C′
B′
A
C
B
D
D′
A′
C′
B′
A
C
B
D
D′
A′
C′
B′
A
C
B
D
D′
A
C
B
A′
B′
C′
∽
(1)
两个相似图形,其中一个图形可以看作是由另一个图形放大或缩小得到的。
猜想:三角形放大后,对应高发生了什么变化?
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应高AD和A'D'.
求证:
A′
C′
B′
A
C
B
D
D′
探究一
相似三角形对应高的比等于相似比
证明:∵△ABC∽△A'B'C',
∴∠B=∠B'.
∵AD和A'D'分别是△ABC和△A'B'C'对应边上的高,
∴∠ADB=∠A'D'B'=900
∴△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
结论:相似三角形对应高的比等于相似比
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应中线AD和A'D'.
求证:
A′
C′
B′
A
C
B
D
D′
探究二
相似三角形对应中线的比等于相似比
证明:∵△ABC∽△A'B'C',
∴∠B=∠B',
∴在△ABD与△A'B'D'中,
△ABD∽△A'B'D'.
∴ .
A
C
B
D
A′
C′
B′
D′
∵AD和A'D'分别是△ABC和△A'B'C'对应边上的中线,
结论:相似三角形对应中线的比等于相似比
已知:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应角平分线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
探究三
相似三角形对应角平分线的比等于相似比
求证:
∴∠BAD= ∠BAC,
∴在△ABD与△A'B'D'中,
△ABD∽△A'B'D'.
∴
证明:∵△ABC∽△A'B'C',
∴∠B=∠B',∠BAC=∠B'A'C'.
∵AD和A'D'分别是∠BAC和∠B'A'C'的平分线,
A′
C′
B′
A
C
B
D′
D
结论:相似三角形对应角平分线的比等于相似比
null
新知归纳
这样我们得到
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有
相似三角形对应线段的比等于相似比.
null
新知归纳
几何语言
∵△ABC∽△AB'C',
AD和A'D'分别是它们的高.
D
D′
∴
相似三角形对应线段的比等于相似比
null
解:设△ABC和△A'B'C'的相似比为k,则
∴AB= kA′B′,BC= kB′C′,AC= kA′C′,
如果△ABC∽△A'B'C',相似比为k,那么△ABC与△A'B'C'的周长比是多少?
结论:相似三角形周长的比等于相似比.
探究四 相似三角形的周长比等于相似比
如图,△ABC∽△A′B′C′,相似比为k,△ABC与△A′B′C′的面积比是多少?
解:
结论:相似三角形面积的比等于相似比的平方.
A′
C′
B′
A
C
B
D
D′
探究五
相似三角形面积的比等于相似比的平方.
(1)已知ΔABC与ΔA'B'C' 的相似比为2:3,
则周长比为 ,对应边上中线之比为 ,
面积之比为 。
(2)已知ΔABC∽ΔA'B'C',且面积之比为9:4,
则周长之比为 ,相似比为 ,
对应边上的高线之比 。
2:3
4:9
3:2
3: 2
3:2
2:3
运用新知
1.判断题(正确的画“√”,错误的画“Χ”)
(1)一个三角形各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍;( )
(2)一个三角形各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.( )
√
Χ
《教材》P39 练习:
解:∵ △ABC ∽△DEF,
D
E
F
H
例1 已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG= 4.8 cm. 求 EH 的长.
∴ (相似三角形对应角平分线的比等于相似比),
∴ ,解得 EH = 3.2.
A
G
B
C
典例精析
∴ EH 的长为 3.2 cm.
null
相似三角形的面积比等于相似比的平方
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
例2 如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
挑战自我
如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN的边长为xcm。
∵PN∥BC,∴△APN∽ △ABC
∴
AE
AD
=
PN
BC
即
得 x=48cm。
答:正方形零件的边长为48cm。
80–x
80
=
x
120
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
课堂小结
相似三角形的性质有哪些?
布置作业
课堂作业
课本第58页第11题
同学们,再见!
