人教版七年级数学下册 5.3 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.3 平行线的性质 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览





文档简介
平行线的性质 同步练习
一、选择题
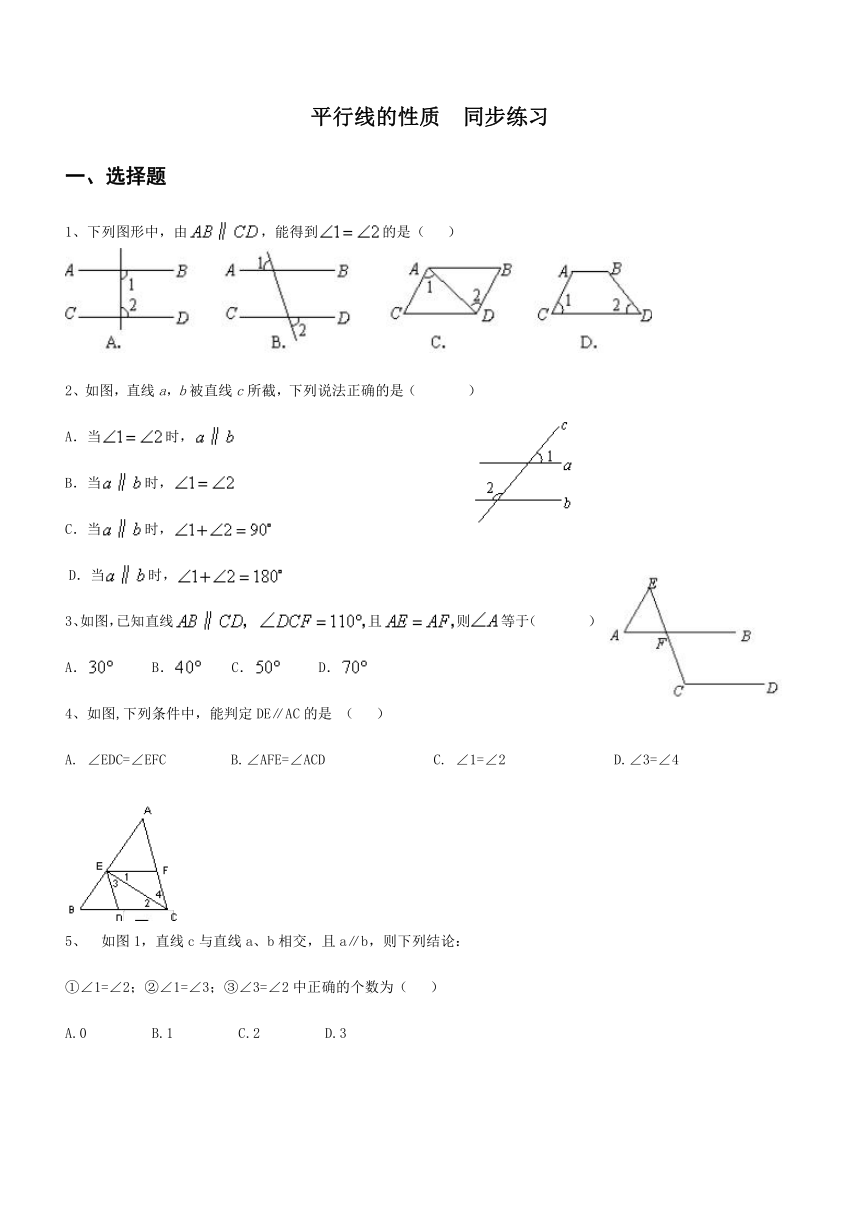
1、下列图形中,由,能得到的是(? )
2、如图,直线a,b被直线c所截,下列说法正确的是(??? )
A.当时,???
B.当时,
C.当时,?
D.当时,
3、如图,已知直线且则等于(??? )
A. B. C.?? D.
4、如图,下列条件中,能判定DE∥AC的是 (? )
A. ∠EDC=∠EFC???? B.∠AFE=∠ACD??????? C. ∠1=∠2??????? D.∠3=∠4
5、?如图1,直线c与直线a、b相交,且a∥b,则下列结论:
①∠1=∠2;②∠1=∠3;③∠3=∠2中正确的个数为(? )
A.0???? B.1???? C.2???? D.3
6、如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于
A.30°??? B.40°??? C.60°?? D.70°
7、如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是( )
A.40°?? B.60°???? C.70°?????? D.80°???? ?????
8、如图,周董从A处出发沿北偏东60°方向行走至B处,又沿北偏西方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是(??? ).
A.右转80°????? B.左转80°? ??? C.右转100°??????? D.左转100°?
9、如图,AB∥CD.若∠2是∠1的两倍,则∠2等于( )
A.60°?? B.90°?? C.120°?? D.150°
10、 和相交于点,则(??? )
A.? ? ??????B.???? C. ???????? D.
11、,于交于,已知,则(??? )
A.20°???? B.60°???? C.30°??? D.45°
12、如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于?( )
???
A. 70°????? B. 65°??? ???? C. 50°??? ?? D. 25°? ?????????
二、填空题
13、如图,直线DE交∠ABC的边BA于点D,若DE∥BC,∠B=70°,则∠ADE的度数是 .?
14、如图,AD//BC,BD平分∠ABC,∠A :∠ABC=2:1,则∠ADB=???? °
15、如图,直线a∥b,l与a、b交于E、F点,PF平分∠EFD交a于P点,若∠1 = 70°,则∠2 =??? .
16、如图,a//b,∠1=(3x+20)0,∠2=(2x+10)0,那么∠3=????? 0.
?
17、如图,若AD∥CE,,则的度数为????? 。
?
18、如图AB∥CD,直线EF分别交AB、CD于E、F,且EG平分∠AEF,∠1=34?则∠2=? ?????.
19、如图,O是△ABC内一点,OD∥AB,OE∥BC,OF∥AC,∠B=45°,∠C=75°,则∠DOE=????? ,∠EOF=????? ,∠FOD=????? .
三、简答题
20、已知,如图,∠1=∠2,∠3=∠4,试说明的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由。
∵∠1=∠2(已知),
=∠1 (?????????? ),
∴=∠2 (等量代换),
∴ (?????????? ),
∴= (???????? ),
∵∠3=∠4(已知)
∴-∠4=-∠3 (等式的基本性质),
即∠=
∴ (?????????? ).
21、如图,已知∠BAP与∠APD互补,∠1=∠2,证明:∠E=∠F.
22、将一副直角三角板如图放置,已知AE∥BC,求∠AFD的度数.
23、如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
(1)求证:AE∥CD;????????????? ????????
(2)求∠B的度数.
24、已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图).
(1)CE∥BF这一结论对吗?为什么?
(2)你能得∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
25、?“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN= ?? °;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
参考答案
一、选择题
1、B;2、D;3、B;4、D;5、D;6、A;7、C;8、A;9、D.;10、B;11、C;12、C
二、填空题
13、70°
14、30°
15、35°
16、70°;??
17、??????? ?
18、112° ???
19、35°,105°,120°.
三、简答题
20、
;
;
;
.
?
21、解:∵∠BAP与∠APD互补(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠BAP=∠APC(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠BAP﹣∠1=∠APC﹣∠2(等式的性质1)
即∠3=∠4
∴AE∥PF(内错角相等,两直线平行 )
∴∠E=∠F(两直线平行,内错角相等).
?22、解∵ AE‖BC,所以∠EAD=∠ADB=45°
∴∠FDC=90°-45°=45°
∴∠DFC=180°-∠FDC-∠FCD
???????? =180°-45°-30°=105°
∴ ∠AFD=180°-∠DFC=75°(方法不唯一)
23、(1)证明:∵AD∥BC,
∴∠D+∠C=180°,
∵∠EAD=∠C,
∴∠EAD+∠D=180°,
∴AE∥CD;?????????
(2)∵AE∥CD,
∴∠AEB=∠C,
∵∠FEC=∠BAE,
∴∠B=∠EFC=50°.………………(8分)
24、(1)正确.
∵∠1=∠4,∠1=∠2,
∴∠2=∠4,
∴CE∥BF;
(2)∠B=∠3,∠A=∠D成立.
∵由(1)得,CE∥BF,
∴∠3=∠C.
∵∠B=∠C,
∴∠B=∠3,
∴AB∥CD,
∴∠A=∠D.
25、?解:(1)60°
(2)设A灯转动t秒,两灯的光束互相平行,
①当0<t<90时,如图1,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD
∴2t=1?(30+t),
解得 t=30;
②当90<t<150时,如图2,
∵PQ∥MN,
∴∠PBD+∠BDA=180°,
∵AC∥BD,
∴∠CAN=∠BDA
∴∠PBD+∠CAN=180°
∴1?(30+t)+(2t﹣180)=180,
解得? t=110,
综上所述,当t=30秒或110秒时,两灯的光束互相平行;
(3)∠BAC和∠BCD关系不会变化.
理由:设灯A射线转动时间为t秒,
∵∠CAN=180°﹣2t,
∴∠BAC=60°﹣(180°﹣2t)=2t﹣120°,
又∵∠ABC=120°﹣t,
∴∠BCA=180°﹣∠ABC﹣∠BAC=180°﹣t,而∠ACD=120°,
∴∠BCD=120°﹣∠BCD=120°﹣(180°﹣t)=t﹣60°,
∴∠BAC:∠BCD=2:1,
即∠BAC=2∠BCD,
∴∠BAC和∠BCD关系不会变化
