人教版七年级数学下册 5.2 平行线及其判定 同步练习(含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.2 平行线及其判定 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览


文档简介
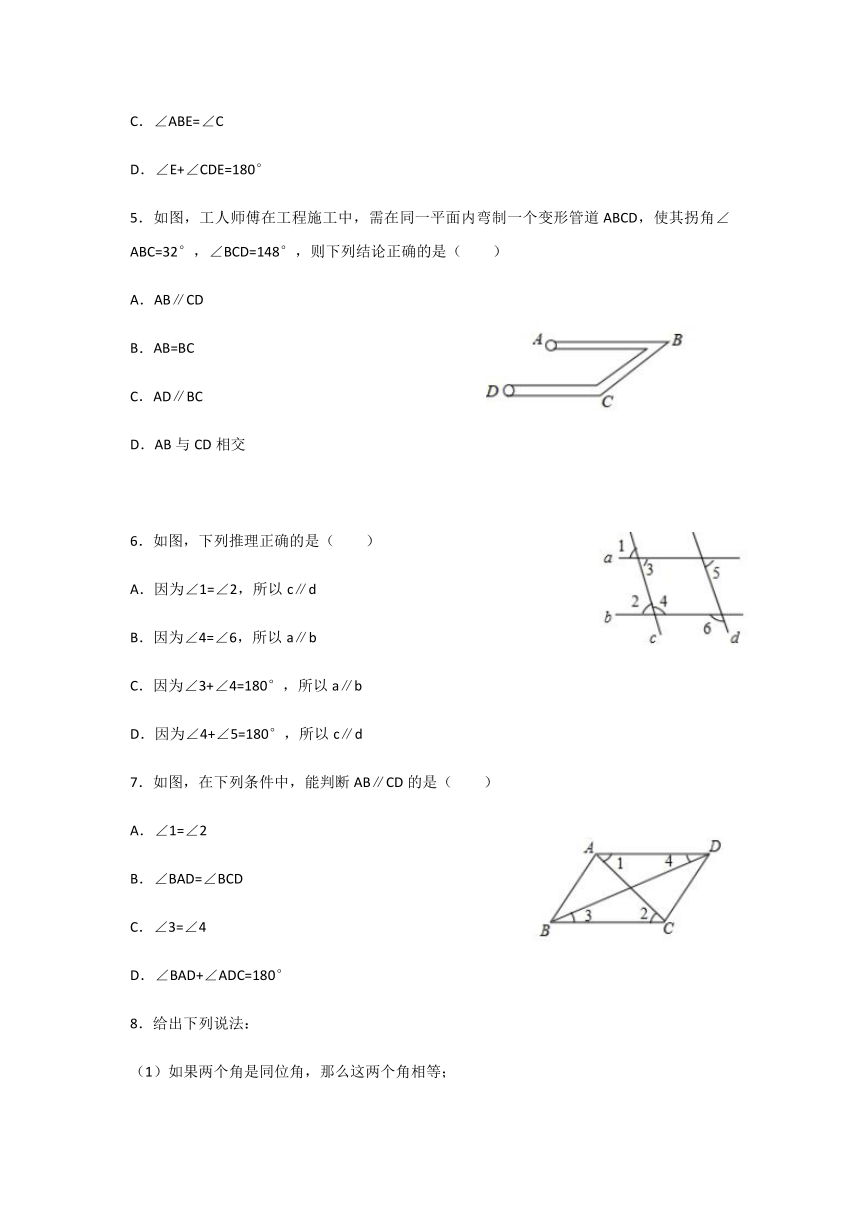
平行线及其判定 同步练习
一.选择题(共12小题)
1.下列语句中,正确的有( )
(1)两点之间直线最短 (2)同位角相等
(3)不相交的两条直线互相平行 (4)垂直于同一条直线的两直线互相平行
(5)同一平面内,过一点有且仅有一条直线平行于已知直线
A.0个 B.1个 C.2个 D.3个
2.如图,能判定AB∥CD的条件是( )
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.∠2=∠4
3.如图,已知点B在射线DE上,若∠ABE=∠CDE,则AB与CD之间的位置关系是( )
A.平行
B.相交
C.平行或相交
D.无法判断
4.如图,能判定AB∥DE的条件是( )
A.∠A=∠ADE
B.∠AFB=∠ADC
C.∠ABE=∠C
D.∠E+∠CDE=180°
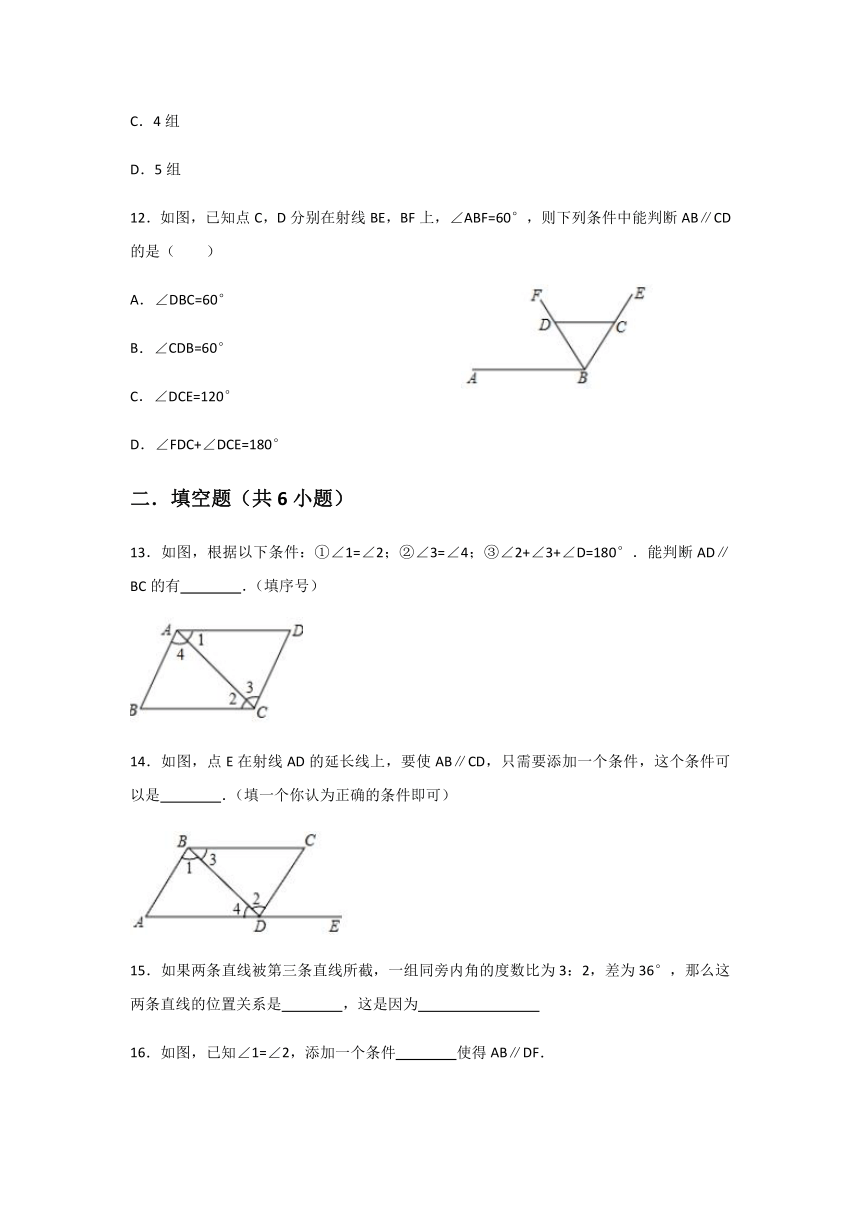
5.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=32°,∠BCD=148°,则下列结论正确的是( )
A.AB∥CD
B.AB=BC
C.AD∥BC
D.AB与CD相交
6.如图,下列推理正确的是( )
A.因为∠1=∠2,所以c∥d
B.因为∠4=∠6,所以a∥b
C.因为∠3+∠4=180°,所以a∥b
D.因为∠4+∠5=180°,所以c∥d
7.如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2
B.∠BAD=∠BCD
C.∠3=∠4
D.∠BAD+∠ADC=180°
8.给出下列说法:
(1)如果两个角是同位角,那么这两个角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)直线外一点与直线上各点的连接的所有线段中,垂线段最短.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
9.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.②③④
B.②③⑤
C.②④⑤
D.②④
10.如图,下列四个条件中,能判断DE∥AC的是( )
A.∠2=∠4
B.∠3=∠4
C.∠AFE=∠ACB
D.∠BED=∠C
11.如图,已知∠1=∠2=∠3=∠4,则图中平行的线有( )
A.2组
B.3组
C.4组
D.5组
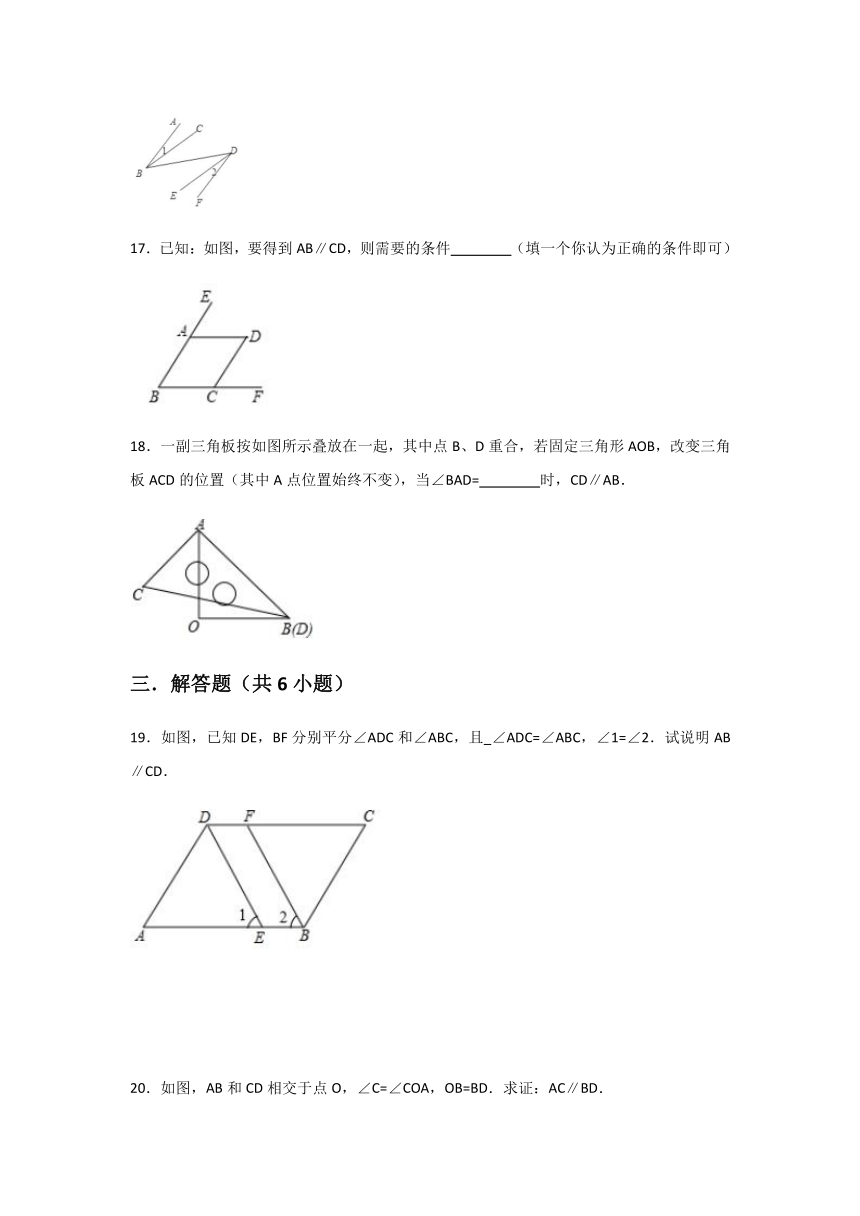
12.如图,已知点C,D分别在射线BE,BF上,∠ABF=60°,则下列条件中能判断AB∥CD的是( )
A.∠DBC=60°
B.∠CDB=60°
C.∠DCE=120°
D.∠FDC+∠DCE=180°
二.填空题(共6小题)
13.如图,根据以下条件:①∠1=∠2;②∠3=∠4;③∠2+∠3+∠D=180°.能判断AD∥BC的有 .(填序号)
14.如图,点E在射线AD的延长线上,要使AB∥CD,只需要添加一个条件,这个条件可以是 .(填一个你认为正确的条件即可)
15.如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是 ,这是因为
16.如图,已知∠1=∠2,添加一个条件 使得AB∥DF.
17.已知:如图,要得到AB∥CD,则需要的条件 (填一个你认为正确的条件即可)
18.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD= 时,CD∥AB.
三.解答题(共6小题)
19.如图,已知DE,BF分别平分∠ADC和∠ABC,且_∠ADC=∠ABC,∠1=∠2.试说明AB∥CD.
20.如图,AB和CD相交于点O,∠C=∠COA,OB=BD.求证:AC∥BD.
21.如图,BE平分∠ABD,DE平分∠CDB相交于AC上一点E,∠BED=90°,求证:AB∥CD.
22.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED,试说明:(1)AB∥CD (2)DE∥BF.
23.如图,∠ADE=∠DEF,∠EFC+∠C=180°,试问AD与BC平行吗?为什么?
24.如图,∠DAC+∠ACB=180°,CE平分∠BCF,∠FEC=∠FCE,∠DAC=3∠BCF,∠ACF=20°.
(1)求证:AD∥EF;
(2)求∠DAC、∠FEC的度数.
参考答案
1-5:ADAAA 6-10:CDCCB 11-12:CB
13、①③
14、∠l=∠2或∠A=∠CDE或∠C+∠ABC=180°等
15、平行;同旁内角互补
16、∠CBD=∠BDE
17、∠EAD=∠ADC(答案不唯一)
18、30°或150°
19、:∵DE,BF分别平分∠ADC和∠ABC,
∴∠FDE=0.5∠ADC,∠2=0.5∠ABC,
∵∠ADC=∠ABC,
∴∠FDE=∠2,
∵∠1=∠2,
∴∠1=∠FDE,
∴AB∥CD.
20、:∵OB=BD,
∴∠D=∠BOD,
∵∠C=∠COA,∠COA=∠BOD(对顶角相等),
∴∠C=∠D.
∴AC∥BD(内错角相等,两直线平行).
21、:在△BDE中,∵∠BED=90°,∠BED+∠EBD+∠EDB=180°,
∴∠EBD+∠EDB=180°-∠BED=180°-90°=90°.
又∵BE平分∠ABD,DE平分∠CDB,
∴∠ABD=2∠EBD,∠CDB=2∠EDB,
∴∠ABD+∠CDB=2(∠EBD+∠EDB)=2×90°=180°,
∴AB∥CD.
22、:(1)∵DE平分∠CDA,
∴∠ADE=∠EDC,
而∠ADE=∠AED,
∴∠EDC=∠AED,
∴AB∥CD;
(2)∵BF平分∠CBA,
∴∠ABF=∠ABC,
∵∠AED=∠ADE=∠ADC,
而∠CDA=∠CBA,
∴∠AED=∠ABF,
∴DE∥BF.
23、结论:AD∥BC.
理由:如图,∵∠ADE=∠DEF(已知),
∴AD∥EF(内错角相等,两直线平行),
∵∠EFC+∠C=180°(已知),
∴EF∥BC(同旁内角互补,两直线平行),
∴AD∥BC(平行于同一条直线的两条直线平行)
24、1)证明:∵∠DAC+∠ACB=180°,
∴BC∥AD,
∵CE平分∠BCF,
∴∠ECB=∠FCE,
∵∠FEC=∠FCE,
∴∠FEC=∠BCE,
∴BC∥EF,
∴AD∥EF;
(2)设∠BCE=∠ECF=0.5∠BCF=x.由∠DAC=3∠BCF可得出∠DAC=6x,则
6x+x+x+20°=180°,
解得x=20°,
则∠DAC的度数为120°,∠FEC的度数为20°.
