华东师大版数学七年级下册 8.1认识不等式 课件(23张ppt)
文档属性
| 名称 | 华东师大版数学七年级下册 8.1认识不等式 课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览








文档简介
(共69张PPT)
8.1 认识不等式
学习目标
1、知道什么叫做不等式,并会举例。
2、理解不等式的解的意义,能列举和验证不等式的解。
3、能根据题义列出不等式。
4、能够利用不等式建立模型并解决实际问题
学习重点:让学生理解不等式和不等式的解的意义,能正确列出不等式;
学习难点:准
确应用不等号,正确理解不等式的解;
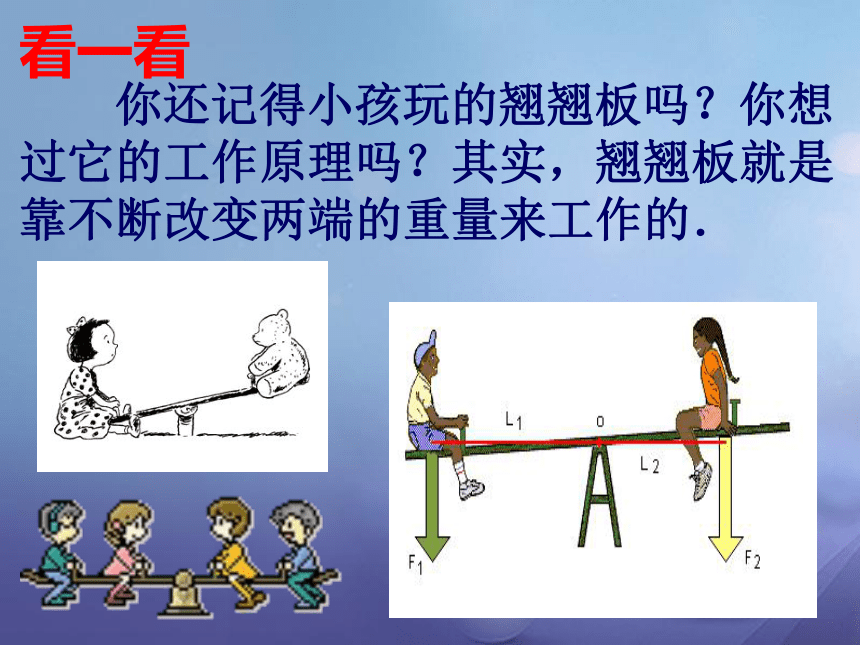
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?其实,翘翘板就是靠不断改变两端的重量来工作的.
看一看
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:不等式.
世纪公园的票价是:每人5元,一次购票满30张可少收1元.某班有27名少先队员去世公园进行活动.当领队王小华准备好了零钱到售票处买了27张票时,爱动脑的李敏同纪学喊住了王小华,提议买30张票.但有的同学不明白.明明只有27个人,买30张票,岂不浪费吗?
那么,究竟李敏的提议对不对呢?是不是真的浪费呢
问题1:小华和小敏两人的建议,到底谁的比较合算呢?为什么?
探索过程如下:
小华:买27张票,付款: ;
小敏:买30张票,付款: _________
显然 < ____________
问题2: 我们只用120元就买了30张票,
买30张票,我们不仅省钱,而且多
买了票,那么剩下的3张票如何处理呢?
问题3:买30张票比买27张票付的款还要少,这是不是说任何情况下都是多买票反而花钱少?
问题4:至少要有多少人去参观,多买票反而合算呢?能否用数学知识来解决?
假设有x人要去公园游园.
(1)如果x≥30,则按实际人数买票,每张票只付4元,需花 元。
(2)如果x<30,那么:按实际人数买票x张,要付款 元;
买30张票,要付款4×30=120(元).如果买30张票合算,则120<5x.
问题5:如果买30张票合算,x取哪些数值时,120<5x成立?(填课本P51图表)
填一填
由上表可见,当x=_______时,不等式120<5x成立.也就是说,少于30人时,至少要有____人进公园,买30张票反而合算.
110
120>5x
不成立
115
120>5x
不成立
120
120=5x
120<5x
120<5x
120<5x
120<5x
不成立
成立
成立
成 立
成 立
125
130
130
130
25
25
x 5x 比较120与5x的大小 120<5x成立吗?
21 105 120>5x 不成立
22
23
24
25
26
27 135 120<5x 成 立
28
29
注: “不大于” 指的是 “ ”,
通常用 符号 “ ≤” 表示。
类似地,“不小于”指的是“等于或大于”。
通常用符号“≥”表示。(读作:“大于或等于”)。
等于或小于
例如,x 不大于10 可以表示为:x≤10(读作:“x小于或等于10”)。
概括:
1、像120<135、x<30、120<5x,这些叫做不等式。
2、常用的不等号有:
自学检测:
1、判断下列各式中哪些是不等式,哪些不是。(是打“√”不是打“×”)
⑴ x+1=2 ( ) ⑵ 5x-3>1 ( ) ⑶ x-6 ( )
⑷ 11x-4≤6( ) ⑸ 7>4 ( ) ⑹2x-y≥0 ( )
2、用“<”或“>”号填空:
(1) -7____-5; (2) (-3) ×4____34;
(3) (-4) × 2____(-3) × 2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
3、用适当的不等式符号表示下列关系:
(1) a是负数; (2) a是非负数;
(3) a与b的和小于5; (4) x与2的差大于-1 (5) x的4倍不大于7; (6) y的一半不小于3.
4、判断下列各数,哪些是不等式x+2>4的解。
(是打“√”不是打“×”)
⑴ -1;( ) ⑵ -3;( ) ⑶ -2.5;( )
⑷ 0;( ) ⑸ 1;( ) ⑹ 2;( )
⑺ 3;( ) ⑻ 3.5;( ) ⑼ 4;( )
能力提升
例1:用不等式表示下列关系,并写出两个满足不等式的数: (1)x的一半不大于-2 (2)y与3的差大于0.5 (3)a是负数; (4)b是非负数;
能力巩固
选择题
1、绝对值大于1且小于3的整数是( ) A、2 B、-2 C、±2 D、不能确定
2、无论x取何值,下列不等式总成立的是( ) A、x+1>x+3 B 、(x-3)2≥0 C、3x>1 D、3x+2>x+1
3、有理数在数轴上的位置如图所示,则下列各式中成立的是
( )
A、a+b>0 B、b-c<0
C、ab> 0 D、a/b>0
二、填空题:
1.用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
2.表述下列不等式的意义:
若x<0,则表示______________.
若x≥0,则表示______________.
若x-y>0,则表示_____________.
若x≥y,则表示_____________.
3.请你用不等式表示下列关系
x与y同号______________. x与y异号______________.
4.下列各式哪些是不等式?(是的打“√”不是打“×”)。
8<9.( )a+b=0.( )4-2x。( )x2-y2≥0( )
5.下列各数:0,-3,3,4,-0.5,-20,-4中, ________ __是
方程x+3=0的解; __________是不等式x+3>0的解;
__________是不等式2x+3
6.写出不等式x-5>0的三个解______ _
7.冬天到了,小华准备用自己平时节约的30元钱为乡下的
爷爷奶奶和自己买手套与袜子.已知一副手套5元钱,一双
袜子4元钱,他先买了3双袜子.如果设他还能买x副手套,那
么根据题意,可得到不等式_______________.
三、用不等式表示:
(1) 与1的和是正数;
(2) 的2倍与1的和大于3;
(3) 的一半与4的差的绝对值不小于 ;
(4) 的2倍减去1不小于 与3的和;
(5) 与 的平方和是非负数;
(6) 的2倍加上3的和大于-2且小于4;
四、能力拓展
学校组织学生观看电影,某电影院票价每张12元,
50人以上(含50人)的团体票可享受8折优惠,现
有45名学生一起到电影院看电影,为享受8折优惠,
必须按50人购团体票。
⑴请问他们购买团体票是否比不打折而按45人购票
便宜;
⑵若学生到该电影院人数不足50人,应至少有多少
人买团体票比不打折而按实际人数购票便宜。
解:⑴按实际45人购票需付钱_________ 元,如果按50人购买团体票则需付钱50×12×80%=480元,所以购买
票便宜。
⑵设有x人到电影院观看电影,当x_____时,按实际人数买票______张,需付款_______元,而按团体票购票需付款________元,
如果买团体票合算,那么应有不等式________________,
由①得,当x=45时,上式成立,让我们再取一些数据试一试,将结果填入下表:
由上表可见,至少要__________人时进电影院,购团体票才合算。
x 12x 比较480与12x的大小 48<12x成立吗?
30
40
41
42
想想这节课你有哪些收获?
小结:
1。生活中处处存在不等关系,我们可以用
不等式来解决生活中的实际问题
2。检验一个数是不是不等式的解,应代入
不等式中检验
3。注意:不等式的解与一元一次方程的解
是有区别的.不等式的解是不确定的,是
一个范围,而一元一次方程的解则是一个
具体的数值.
8.1 认识不等式
学习目标
1、知道什么叫做不等式,并会举例。
2、理解不等式的解的意义,能列举和验证不等式的解。
3、能根据题义列出不等式。
4、能够利用不等式建立模型并解决实际问题
学习重点:让学生理解不等式和不等式的解的意义,能正确列出不等式;
学习难点:准
确应用不等号,正确理解不等式的解;
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?其实,翘翘板就是靠不断改变两端的重量来工作的.
看一看
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:不等式.
世纪公园的票价是:每人5元,一次购票满30张可少收1元.某班有27名少先队员去世公园进行活动.当领队王小华准备好了零钱到售票处买了27张票时,爱动脑的李敏同纪学喊住了王小华,提议买30张票.但有的同学不明白.明明只有27个人,买30张票,岂不浪费吗?
那么,究竟李敏的提议对不对呢?是不是真的浪费呢
问题1:小华和小敏两人的建议,到底谁的比较合算呢?为什么?
探索过程如下:
小华:买27张票,付款: ;
小敏:买30张票,付款: _________
显然 < ____________
问题2: 我们只用120元就买了30张票,
买30张票,我们不仅省钱,而且多
买了票,那么剩下的3张票如何处理呢?
问题3:买30张票比买27张票付的款还要少,这是不是说任何情况下都是多买票反而花钱少?
问题4:至少要有多少人去参观,多买票反而合算呢?能否用数学知识来解决?
假设有x人要去公园游园.
(1)如果x≥30,则按实际人数买票,每张票只付4元,需花 元。
(2)如果x<30,那么:按实际人数买票x张,要付款 元;
买30张票,要付款4×30=120(元).如果买30张票合算,则120<5x.
问题5:如果买30张票合算,x取哪些数值时,120<5x成立?(填课本P51图表)
填一填
由上表可见,当x=_______时,不等式120<5x成立.也就是说,少于30人时,至少要有____人进公园,买30张票反而合算.
110
120>5x
不成立
115
120>5x
不成立
120
120=5x
120<5x
120<5x
120<5x
120<5x
不成立
成立
成立
成 立
成 立
125
130
130
130
25
25
x 5x 比较120与5x的大小 120<5x成立吗?
21 105 120>5x 不成立
22
23
24
25
26
27 135 120<5x 成 立
28
29
注: “不大于” 指的是 “ ”,
通常用 符号 “ ≤” 表示。
类似地,“不小于”指的是“等于或大于”。
通常用符号“≥”表示。(读作:“大于或等于”)。
等于或小于
例如,x 不大于10 可以表示为:x≤10(读作:“x小于或等于10”)。
概括:
1、像120<135、x<30、120<5x,这些叫做不等式。
2、常用的不等号有:
自学检测:
1、判断下列各式中哪些是不等式,哪些不是。(是打“√”不是打“×”)
⑴ x+1=2 ( ) ⑵ 5x-3>1 ( ) ⑶ x-6 ( )
⑷ 11x-4≤6( ) ⑸ 7>4 ( ) ⑹2x-y≥0 ( )
2、用“<”或“>”号填空:
(1) -7____-5; (2) (-3) ×4____34;
(3) (-4) × 2____(-3) × 2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
3、用适当的不等式符号表示下列关系:
(1) a是负数; (2) a是非负数;
(3) a与b的和小于5; (4) x与2的差大于-1 (5) x的4倍不大于7; (6) y的一半不小于3.
4、判断下列各数,哪些是不等式x+2>4的解。
(是打“√”不是打“×”)
⑴ -1;( ) ⑵ -3;( ) ⑶ -2.5;( )
⑷ 0;( ) ⑸ 1;( ) ⑹ 2;( )
⑺ 3;( ) ⑻ 3.5;( ) ⑼ 4;( )
能力提升
例1:用不等式表示下列关系,并写出两个满足不等式的数: (1)x的一半不大于-2 (2)y与3的差大于0.5 (3)a是负数; (4)b是非负数;
能力巩固
选择题
1、绝对值大于1且小于3的整数是( ) A、2 B、-2 C、±2 D、不能确定
2、无论x取何值,下列不等式总成立的是( ) A、x+1>x+3 B 、(x-3)2≥0 C、3x>1 D、3x+2>x+1
3、有理数在数轴上的位置如图所示,则下列各式中成立的是
( )
A、a+b>0 B、b-c<0
C、ab> 0 D、a/b>0
二、填空题:
1.用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
2.表述下列不等式的意义:
若x<0,则表示______________.
若x≥0,则表示______________.
若x-y>0,则表示_____________.
若x≥y,则表示_____________.
3.请你用不等式表示下列关系
x与y同号______________. x与y异号______________.
4.下列各式哪些是不等式?(是的打“√”不是打“×”)。
8<9.( )a+b=0.( )4-2x。( )x2-y2≥0( )
5.下列各数:0,-3,3,4,-0.5,-20,-4中, ________ __是
方程x+3=0的解; __________是不等式x+3>0的解;
__________是不等式2x+3
6.写出不等式x-5>0的三个解______ _
7.冬天到了,小华准备用自己平时节约的30元钱为乡下的
爷爷奶奶和自己买手套与袜子.已知一副手套5元钱,一双
袜子4元钱,他先买了3双袜子.如果设他还能买x副手套,那
么根据题意,可得到不等式_______________.
三、用不等式表示:
(1) 与1的和是正数;
(2) 的2倍与1的和大于3;
(3) 的一半与4的差的绝对值不小于 ;
(4) 的2倍减去1不小于 与3的和;
(5) 与 的平方和是非负数;
(6) 的2倍加上3的和大于-2且小于4;
四、能力拓展
学校组织学生观看电影,某电影院票价每张12元,
50人以上(含50人)的团体票可享受8折优惠,现
有45名学生一起到电影院看电影,为享受8折优惠,
必须按50人购团体票。
⑴请问他们购买团体票是否比不打折而按45人购票
便宜;
⑵若学生到该电影院人数不足50人,应至少有多少
人买团体票比不打折而按实际人数购票便宜。
解:⑴按实际45人购票需付钱_________ 元,如果按50人购买团体票则需付钱50×12×80%=480元,所以购买
票便宜。
⑵设有x人到电影院观看电影,当x_____时,按实际人数买票______张,需付款_______元,而按团体票购票需付款________元,
如果买团体票合算,那么应有不等式________________,
由①得,当x=45时,上式成立,让我们再取一些数据试一试,将结果填入下表:
由上表可见,至少要__________人时进电影院,购团体票才合算。
x 12x 比较480与12x的大小 48<12x成立吗?
30
40
41
42
想想这节课你有哪些收获?
小结:
1。生活中处处存在不等关系,我们可以用
不等式来解决生活中的实际问题
2。检验一个数是不是不等式的解,应代入
不等式中检验
3。注意:不等式的解与一元一次方程的解
是有区别的.不等式的解是不确定的,是
一个范围,而一元一次方程的解则是一个
具体的数值.
