北师大版八年级物理下册 9.5探究——使用机械是否省功 达标作业(解析版)
文档属性
| 名称 | 北师大版八年级物理下册 9.5探究——使用机械是否省功 达标作业(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 503.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-09 18:55:38 | ||
图片预览



文档简介
9.5探究——使用机械是否省
功达标作业(解析版)
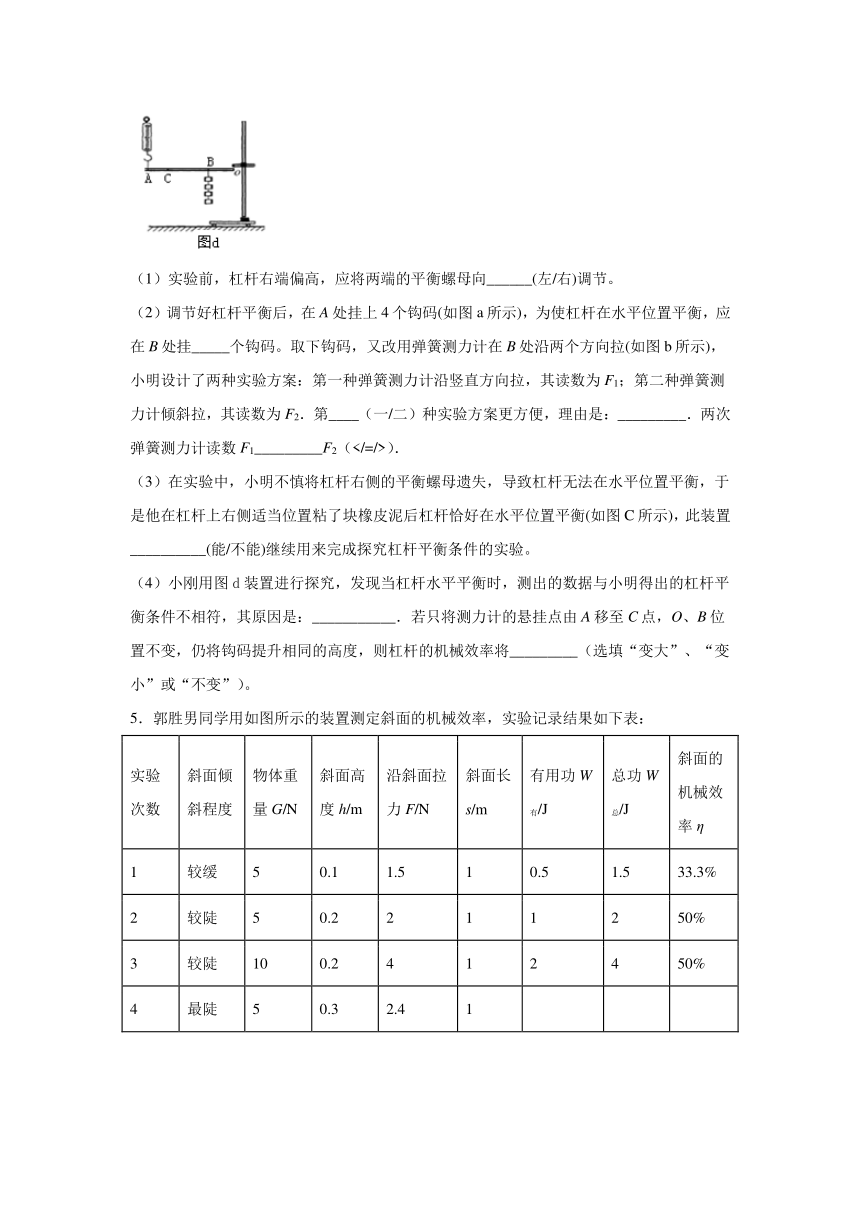
1.如图所示,斜面长3m,高为1m,工人用400N的力沿斜面方向将重为840N的箱子推到车上,则有用功为________J,总功为________J,斜面的机械效率为________.如果斜面摩擦不计,则斜面的机械效率为________,沿斜面的推力大小为________.
2.装卸工人用如图所示的滑轮组气提升重为1000N的货物,所用的拉力为600N,绳子自由端在50s内被拉下2m,在此过程中拉力所做的有用功为_____J,拉力做功的功率为_____W,滑轮组的机械效率是_____%。若测量拉力时弹簧测力计保持静止,则测出的机械效率与真实值相比_____(选填“偏大"、“偏小”或“相同")。
3.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端,斜面高1m,长2m,物体重500N,平行于斜面的拉力200N,所用时间10s.在此过程中,物体动能_______(选填“增大”、“减小”或“不变”).重力势能_______(选填“增大”、“减小”或“不变”).拉力的功率为_______W,把物体直接提高到斜面顶端做的功为有用功,则这个装置的机械效率为_______.
4.利用带有刻度的均匀杠杆探究“杠杆平衡条件”,实验所用钩码质量均相等.
(1)实验前,杠杆右端偏高,应将两端的平衡螺母向______(左/右)调节。
(2)调节好杠杆平衡后,在A处挂上4个钩码(如图a所示),为使杠杆在水平位置平衡,应在B处挂_____个钩码。取下钩码,又改用弹簧测力计在B处沿两个方向拉(如图b所示),小明设计了两种实验方案:第一种弹簧测力计沿竖直方向拉,其读数为F1;第二种弹簧测力计倾斜拉,其读数为F2.第____(一/二)种实验方案更方便,理由是:_________.两次弹簧测力计读数F1_________F2().
(3)在实验中,小明不慎将杠杆右侧的平衡螺母遗失,导致杠杆无法在水平位置平衡,于是他在杠杆上右侧适当位置粘了块橡皮泥后杠杆恰好在水平位置平衡(如图C所示),此装置__________(能/不能)继续用来完成探究杠杆平衡条件的实验。
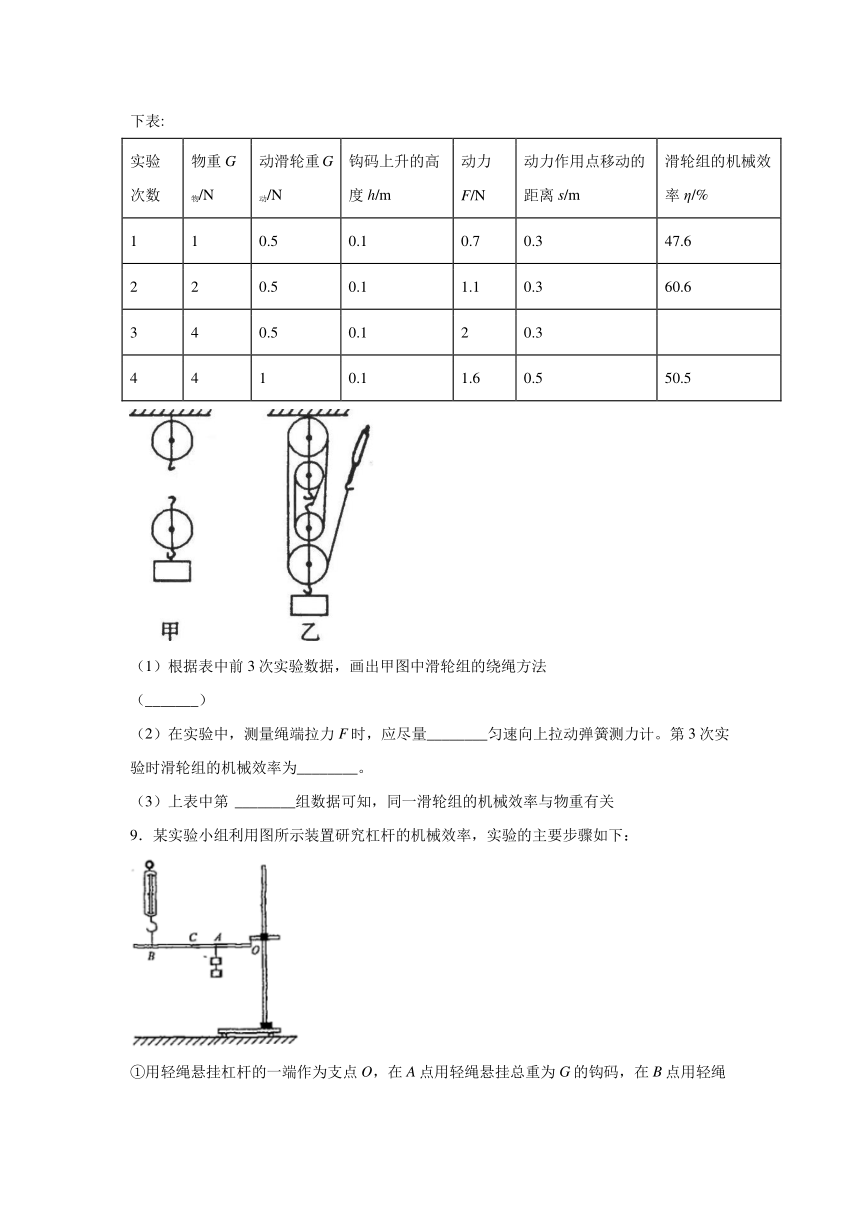
(4)小刚用图d装置进行探究,发现当杠杆水平平衡时,测出的数据与小明得出的杠杆平衡条件不相符,其原因是:___________.若只将测力计的悬挂点由A移至C点,O、B位置不变,仍将钩码提升相同的高度,则杠杆的机械效率将_________(选填“变大”、“变小”或“不变”)。
5.郭胜男同学用如图所示的装置测定斜面的机械效率,实验记录结果如下表:
实验次数
斜面倾斜程度
物体重量G/N
斜面高度h/m
沿斜面拉力F/N
斜面长s/m
有用功W有/J
总功W总/J
斜面的机械效率η
1
较缓
5
0.1
1.5
1
0.5
1.5
33.3%
2
较陡
5
0.2
2
1
1
2
50%
3
较陡
10
0.2
4
1
2
4
50%
4
最陡
5
0.3
2.4
1
(1)根据表格中数据,第四次(最陡)实验的有用功是______J,总功是________J,机械效率是______;
(2)分析数据可知,斜面越陡,机械效率________(选填“越高”、“越低”或“不变”);
(3)分析实验数据还可知道,斜面越陡越___________(选填“省力”或“费力”);
(4)分析实验数据还可知道,斜面的机械效率与物重_______ (填“有关”或“无关”)
(5)第一次实验中,若拉力作用时间是5s,则拉力的功率是___________W。
6.学校升旗仪式上,当升旗手缓缓向下拉绳子时,旗子就会徐徐上升,这是由于旗杆顶部有一个_______滑轮,它能_____________(选填“改变力的方向”或“省力”).如下图是某风景区的一段盘山公路,之所以要把上山的公路修成这般模样,是因为盘山公路相当于简单机械中的__________,使用它可以__________(选填“改变力的方向”或“省力”).
7.如图所示为测定动滑轮机械效率的示意图.用弹簧测力计拉动绳子自由端,将质量为200g的钩码从A位置匀速提升至B位置,同时弹簧测力计从图中的A’位置匀速竖直上升至B’位置,在此过程中,弹簧测力计对绳的拉力为F,弹簧测力计的示数如图所示.请根据所做实验进行分析(g=10N/kg):
(1)弹簧测力计的示数为_____N,拉力F所做的功为____J.
(2)动滑轮的机械效率约为____.(结果保留一位小数)
8.在探究“滑轮组机械效率”时,爱米用图甲测得前3组数据,用图乙测得第4组数据,如下表:
实验次数
物重G物/N
动滑轮重G动/N
钩码上升的高度h/m
动力F/N
动力作用点移动的距离s/m
滑轮组的机械效率η/%
1
1
0.5
0.1
0.7
0.3
47.6
2
2
0.5
0.1
1.1
0.3
60.6
3
4
0.5
0.1
2
0.3
4
4
1
0.1
1.6
0.5
50.5
(1)根据表中前3次实验数据,画出甲图中滑轮组的绕绳方法
(_______)
(2)在实验中,测量绳端拉力F时,应尽量________匀速向上拉动弹簧测力计。第3次实验时滑轮组的机械效率为________。
(3)上表中第 ________组数据可知,同一滑轮组的机械效率与物重有关
9.某实验小组利用图所示装置研究杠杆的机械效率,实验的主要步骤如下:
①用轻绳悬挂杠杆的一端作为支点O,在A点用轻绳悬挂总重为G的钩码,在B点用轻绳竖直悬挂一个弹簧测力计,使杠杆'保持水平,此时弹簧测力计的读数为F0。
②拉动弹簧测力计缓慢上升(保持O点位置不变),在此过程中弹簧测力计的读数为F,利用刻度尺分别测出A、B两点上升的高度为h1、h2,请回答以下问题:
(1)在实验步骤①中,杠杆保持水平平衡,F0×OB=G×___________。
(2)在实验步骤②中,杠杆机械效率的表达式为η=___________。(用题中已知或测量的物理量符号表示)
(3)本次实验中,若提升的钩码重一定,则影响杠杆机械效率的主要因素是_________________。
(4)若只将钩码的悬挂点由A移至C,O、B位置不变,仍将钩码提升相同的高度,则杠杆的机械效率将______(选填“变大”、“变小”或“不变”)。
10.丽丽用一个高度可调节的斜面来探究斜面的省力情况、斜面的机械效率与斜面的倾斜程度之间的关系,如下图所示。她首先测出小车重,然后用弹簧测力计沿斜面拉动小车,调节斜面倾斜角θ的大小多次测量,得到下表所示的数据:
斜面
倾斜角θ
小车重G/N
斜面高
h/m
斜面长
S/m
拉力
F/N
有用功
W有/J
总功
W总/J
机械效率η
12°
5
0.2
1
2.1
1
2.1
48%
30°
5
0.5
1
3.6
2.5
3.6
69%
45°
5
0.7
1
4.3
3.5
4.3
(1) 请你替丽丽在上表中的空格处填上适当的数据______。
(2) 分析上表中的数据,可以得出的探究结论是:斜面倾斜角θ越_______,斜面越省力,斜面的机械效率越_______。
(3) 实验过程中拉力的方向应与斜面__________。
(4) 若想探究斜面的机械效率与物重的关系,则要保持__________不变,斜面的光滑程度不变,,这种研究问题的方法我们称之为____________法。
11.小红和爸爸散步时,看见小区内的一种健身器械坐拉器,如图甲所示,为了对它进行研宄,小红简化了它的结构,画出了它的模型图,如图乙所示。她发现坐在坐拉器座椅上的人,用力向下拉动手柄A时,操作杆AB会绕着转轴O转动,连杆BD拉动杆OC绕转轴O转动,将座椅向上抬起,(g取10N/kg)
(1)小红让爸爸静止坐在坐拉器的座椅上,小红竖直向下拉动手柄,将爸爸抬起经过测量,手柄竖直向下移动30cm,座椅竖直升高9cm,用时5s
①小红利用坐拉器抬起爸爸时,以下说法正确的是____
A.可以省功
B.一定定费力
C.爸爸越重,坐拉器的机械效率越高
D.爸爸被抬得越高,坐拉蕃的机槭效率越高
②若爸爸的质量为60kg,利用坐拉器抬起爸爸的机械效率为90%,则小红抬起爸爸所做功的功率为多少____?
(2)小红想通过图乙的模型,估算自己坐在坐拉器上抬起自己的拉力。图乙中OA:OB=6:1,O′C:O’D=2:1,此时AB杆处于水平位置,BD杆垂直于杆AB和O′′C,BD杆对AB和OC杆的拉力均沿着BD,且大小相等。若手臂对手柄A的拉力方向和人的重力方向视作同一直线,物体间相互作用力的大小相等、方向相反,忽略坐拉器的自重、转动是的摩擦和座椅的尺度,若小红的质量为40kg,则此时小红让自己保持图乙的状态,需要对手柄A施加竖直向下的拉力为多大____?
参考答案
1.840 1200 70% 100% 280
【解析】
人对物体所做的有用功为:
W有=Gh=840N×1m=840J;
人对物体所做的总功:
W总=FL=400N×3m=1200J;
则机械效率:
η=×100%=×100%=70%;
额外功:
W额=W总?W有=1200J?840J=360J;
则摩擦力:
f==120N;
如果斜面摩擦不计,则斜面的机械效率为100%,并且W总=W有,即FL=Gh,则拉力:
F′= ==280N。
【点睛】
根据W有用=Gh求出有用功;根据W总=Fs求出总功;根据η=求出斜面的机械效率。如果斜面摩擦不计,则W总=W有用,即FL=Gh,由此即可求出推力。
2.1000 24 83.3 偏大
【解析】
由图可知滑轮组绳子的有效股数,根据求出货物上升的高度,根据求出拉力所做的有用功,根据求出拉力做的总功,利用求出拉力做功的功率,再利用求出滑轮组的机械效率;若保持静止读数,不用克服摩擦,所测拉力偏小,总功偏小,据此分析。
【详解】
[1]由图可知,n=2,根据可得,货物上升的高度:
,
拉力所做的有用功:
,
[2]拉力做的总功:
,
拉力做功的功率:
,
[3]滑轮组的机械效率:
;
[4]若保持静止读数,不用克服摩擦,所测拉力偏小,总功偏小,测出的机械效率偏大。
3.不变 增大 80 62.5%
【解析】
影响动能的因素为:质量、速度.而影响重力势能的因素为:质量、高度.运用公式,求出总功,再运用,可求功率.运用公式,求出有用功,再运用机械效率的公式,可求出η.
(1)将物体从斜面底端匀速拉到顶端,质量不变,速度不变,则物体的动能不变.
(2)物体沿斜面升高,质量不变,高度变大,所以其重力势能增大.
(3)图中滑轮是动滑轮,则绳端通过的距离为:
;
拉力做功为:
;
拉力的功率为:
(4)此过程的有用功为:
;
这个装置的机械效率为:
;
4.右 3 一 能从杠杆上直接读力臂 < 能 杠杆存在自重 不变
【解析】
(1)[1]实验前,由于杠杆右端偏高,所以,为了使杠杆在水平位置平衡,应将两端的平衡螺母向右调节;
(2)[2]设杠杆上一个小格长度为L,一个钩码重为G,由杠杆平衡条件知道,
4G×3L=nG×4L,
解得n=3,即应在B处挂3个钩码;
[3]力臂等于支点到力的作用线的距离,当杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂可以从杠杆标尺刻度上直接读出来,所以,第一种实验方案更方便;
[4]当杠杆在水平位置平衡时,弹簧测力计的拉力与杠杆垂直,能从杠杆上直接读力臂;
[5]因为第一方案的动力臂要大于第二种方案的动力臂,根据杠杆的平衡条件知道,在阻力和阻力臂都相同的情况下,动力臂越大的越省力,所以,F1 <F2;
(3)[6]根据题意知道,当平衡螺母遗失,粘了橡皮泥后杠杆恰好在水平位置平衡时,则说明测量前杠杆能平衡,故此装置能继续用来完成探究杠杆平衡条件的实验;
(4)[7]小刚用图d装置进行探究,发现当杠杆水平平衡时,测出的数据与小明得出的杠杆平衡条件不相符,其原因是:杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响;
[8]杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,且
W有+W额=W总,
设杠杆重心升高的距离为h,所以,
Gh2 +G杠 h=Fh1 ,
若只将测力计的悬挂点由A移至C点,钩码还升高相同的高度,杠杆上旋的角度不变,杠杆升高的距离h不变,所以,Gh2 +G杠h不变,即Fh1不变。由知道,分母不变,分子不变,所以η不变。
5.1.5 2.4 62.5% 越高 费力 无关 0.3
【解析】
(1)[1]由表格第四次实验数据得到有用功:
W有=Gh=5N×0.3m=1.5J;
[2]总功:
W总=Fs=2.4N×1m=2.4J;
[3]机械效率:
η==62.5%;
(2)[4]分析斜面效率与倾斜程度关系时,应选择斜面倾斜程度不同,其它都相同的实验分析比较。由表中实验序号为1、2、4的数据可知:在物重、斜面粗糙程度相同的情况下,斜面倾斜程度越大斜面机械效率越高;
(3)[5]由表中实验序号为1、2、4的数据可知,斜面倾斜程度越大,需要的拉力越大,即:斜面越陡越费力;
(4)[6]由表中实验序号为2、3的数据可知,斜面的机械效率与物重无关;
(5)[7]由表中实验数据可知,在第一次实验中:W总1=1.5J,拉力功率
P==0.3W。
6.定 改变力的方向 斜面 省力
【解析】
[1]旗杆顶部滑轮的轴固定不动,属于定滑轮;
[2]只能改变力的方向,而不能省力;
[3][4]盘山公路相当于斜面,斜面可以省力。
7.1.2 0.24 83.3%
【解析】
(1)[1][2]如图弹簧测力计的分度值为0.2N,示数为1.2N;测力由25.0cm上升到45.0cm,所以拉力F所做的功为:
;
(2)[3]物体的重为:
钩码由0.0cm上升到10.0cm,所以对钩码做的功为:
;
动滑轮的机械效率约为:
.
8. 竖直 66.7 1、2、3
【解析】
第一空.由前3组实验数据可知s=3h,所以滑轮组由3段绳子承担物重,因此应从动滑轮上面挂钩开始绕起,如图所示:
;
第二空.为能正确在实验中测得绳子自由端的拉力应沿竖直方向匀速拉动弹簧测力计,这样才能准确测出拉力的值;
第三空.第3次实验时滑轮组的机械效率:
;
第四空.根据题意可知,前3组数据是用同一滑轮组做的实验,且物重越大,机械效率越高,所以由表中第1、2、3组数据可知,同一滑轮组的机械效率与物重有关。
9.OA 杠杆的自重 变大
【解析】
第一空.钩码的悬挂点在A点,保持水平平衡时,由杠杠的平衡条件知道, F0×OB=G×OA;
第二空.拉动弹簧测力计缓慢上升过程中,钩码的重力做的是有用功,大小是: W有 =Gh1, 拉力做的是总功,大小是: W总 =Fh2, 所以杠杆的机械效率的表达式是:
第三空.有用功是提升钩码所做的功,额外功主要是克服杠杆重力做的功,影响机械效率的因素主要是有用功和总功所占的比例;提升的钩码重一定,重物升高的距离一定,则说明有用功一定,所以,影响杠杆机械效率的主要因素是杠杆自身的重力;
第四空.杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且 W有 +W额=W总 ; 设杠杆重心升高的距离为h,则有 Gh1 +G杠 h=Fh2 , 由于G、h1 、G杠 都不变,当钩码从A点到C点时,钩码还升高相同的高度,杠杆上旋的角度减小,杠杆升高的距离h变小,则Gh1 +G杠 h变小,所以Fh2 也变小;由知道,杠杆的机械效率变大。
10.81% 小 低 平行 倾斜程度与光滑程度 控制变量
【解析】
(1)=3.5J;=4.3J;η=×100%=×100%=81%.
(2)分析表中的相关数据可以得出:物重和斜面的光滑程度相同时,斜面的倾斜角越小,机械效率越低;斜面的倾斜角越小,越省力。
(3)拉力要克服摩擦力做功,摩擦力方向沿斜面向下,所以拉力方向必须平行斜面,拉力的方向与摩擦力的方向保持在同一条直线上;
(4)若想探究斜面的机械效率与物重的关系,必须控制其它因素不变,只改变物体的重力。本题中根据实验要求,应保持斜面的倾斜角、光滑程度均不变。这里用到的研究方法是控制变量法。
11.(1)①C; ②12W; (2)100N。
【解析】
(1)使用任何机械都不能省功;费力的机械一定省距离;根据机械效率的定义和影响其大小的因素即可判断; 先求出爸爸的体重,然后根据W=Gh求出有用功,再利用效率的公式求出小红抬起爸爸所做的总功,最后根据功率的公式求出小红抬起爸爸所做功的功率: (2)根据杠杆平衡条件得,对于杠杆AOB来说有:FA×OA=FB×OB,对于杠杆O′CD来说有:(G′-FA′)×O′C=FD×O′D,结合题意二者联立即可得出答案。
【详解】
(1)①A、根据功的原理可知,使用任何机械都不能省功,故A错误; B、由题意知,当手柄竖直向下移动30cm,座椅竖直升高9cm,该装置费距离,一定省力,故B错误; C、爸爸越重,有用功占总功的比值越大,则坐拉器的机械效率越高,故C正确; D、手柄竖直向下移动30cm,座椅竖直升高9cm,即二者的比值不变,根据知,坐拉器的机械效率与爸爸的被抬的高度无关,故D错误。
②爸爸的体重:G=mg=60kg×10N/kg=600N,有用功:W有=Gh=600N×0.09m=54J,
小红抬起爸爸所做的总功:,
则小红抬起爸爸所做功的功率:;
(3)小红的重力G′=mg=40kg×10N/kg=400N,
由杠杆平衡条件得,对于杠杆AOB来说:FA×OA=FB×OB,即:---①
对于杠杆O′CD来说有:(G′-FA′)×O′C=FD×O′D,即:---②
由题意知,FB=FD,由于物体间相互作用力的大小相等,即FA=FA′,由①和②得,解得:FA=100N。
功达标作业(解析版)
1.如图所示,斜面长3m,高为1m,工人用400N的力沿斜面方向将重为840N的箱子推到车上,则有用功为________J,总功为________J,斜面的机械效率为________.如果斜面摩擦不计,则斜面的机械效率为________,沿斜面的推力大小为________.
2.装卸工人用如图所示的滑轮组气提升重为1000N的货物,所用的拉力为600N,绳子自由端在50s内被拉下2m,在此过程中拉力所做的有用功为_____J,拉力做功的功率为_____W,滑轮组的机械效率是_____%。若测量拉力时弹簧测力计保持静止,则测出的机械效率与真实值相比_____(选填“偏大"、“偏小”或“相同")。
3.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端,斜面高1m,长2m,物体重500N,平行于斜面的拉力200N,所用时间10s.在此过程中,物体动能_______(选填“增大”、“减小”或“不变”).重力势能_______(选填“增大”、“减小”或“不变”).拉力的功率为_______W,把物体直接提高到斜面顶端做的功为有用功,则这个装置的机械效率为_______.
4.利用带有刻度的均匀杠杆探究“杠杆平衡条件”,实验所用钩码质量均相等.
(1)实验前,杠杆右端偏高,应将两端的平衡螺母向______(左/右)调节。
(2)调节好杠杆平衡后,在A处挂上4个钩码(如图a所示),为使杠杆在水平位置平衡,应在B处挂_____个钩码。取下钩码,又改用弹簧测力计在B处沿两个方向拉(如图b所示),小明设计了两种实验方案:第一种弹簧测力计沿竖直方向拉,其读数为F1;第二种弹簧测力计倾斜拉,其读数为F2.第____(一/二)种实验方案更方便,理由是:_________.两次弹簧测力计读数F1_________F2().
(3)在实验中,小明不慎将杠杆右侧的平衡螺母遗失,导致杠杆无法在水平位置平衡,于是他在杠杆上右侧适当位置粘了块橡皮泥后杠杆恰好在水平位置平衡(如图C所示),此装置__________(能/不能)继续用来完成探究杠杆平衡条件的实验。
(4)小刚用图d装置进行探究,发现当杠杆水平平衡时,测出的数据与小明得出的杠杆平衡条件不相符,其原因是:___________.若只将测力计的悬挂点由A移至C点,O、B位置不变,仍将钩码提升相同的高度,则杠杆的机械效率将_________(选填“变大”、“变小”或“不变”)。
5.郭胜男同学用如图所示的装置测定斜面的机械效率,实验记录结果如下表:
实验次数
斜面倾斜程度
物体重量G/N
斜面高度h/m
沿斜面拉力F/N
斜面长s/m
有用功W有/J
总功W总/J
斜面的机械效率η
1
较缓
5
0.1
1.5
1
0.5
1.5
33.3%
2
较陡
5
0.2
2
1
1
2
50%
3
较陡
10
0.2
4
1
2
4
50%
4
最陡
5
0.3
2.4
1
(1)根据表格中数据,第四次(最陡)实验的有用功是______J,总功是________J,机械效率是______;
(2)分析数据可知,斜面越陡,机械效率________(选填“越高”、“越低”或“不变”);
(3)分析实验数据还可知道,斜面越陡越___________(选填“省力”或“费力”);
(4)分析实验数据还可知道,斜面的机械效率与物重_______ (填“有关”或“无关”)
(5)第一次实验中,若拉力作用时间是5s,则拉力的功率是___________W。
6.学校升旗仪式上,当升旗手缓缓向下拉绳子时,旗子就会徐徐上升,这是由于旗杆顶部有一个_______滑轮,它能_____________(选填“改变力的方向”或“省力”).如下图是某风景区的一段盘山公路,之所以要把上山的公路修成这般模样,是因为盘山公路相当于简单机械中的__________,使用它可以__________(选填“改变力的方向”或“省力”).
7.如图所示为测定动滑轮机械效率的示意图.用弹簧测力计拉动绳子自由端,将质量为200g的钩码从A位置匀速提升至B位置,同时弹簧测力计从图中的A’位置匀速竖直上升至B’位置,在此过程中,弹簧测力计对绳的拉力为F,弹簧测力计的示数如图所示.请根据所做实验进行分析(g=10N/kg):
(1)弹簧测力计的示数为_____N,拉力F所做的功为____J.
(2)动滑轮的机械效率约为____.(结果保留一位小数)
8.在探究“滑轮组机械效率”时,爱米用图甲测得前3组数据,用图乙测得第4组数据,如下表:
实验次数
物重G物/N
动滑轮重G动/N
钩码上升的高度h/m
动力F/N
动力作用点移动的距离s/m
滑轮组的机械效率η/%
1
1
0.5
0.1
0.7
0.3
47.6
2
2
0.5
0.1
1.1
0.3
60.6
3
4
0.5
0.1
2
0.3
4
4
1
0.1
1.6
0.5
50.5
(1)根据表中前3次实验数据,画出甲图中滑轮组的绕绳方法
(_______)
(2)在实验中,测量绳端拉力F时,应尽量________匀速向上拉动弹簧测力计。第3次实验时滑轮组的机械效率为________。
(3)上表中第 ________组数据可知,同一滑轮组的机械效率与物重有关
9.某实验小组利用图所示装置研究杠杆的机械效率,实验的主要步骤如下:
①用轻绳悬挂杠杆的一端作为支点O,在A点用轻绳悬挂总重为G的钩码,在B点用轻绳竖直悬挂一个弹簧测力计,使杠杆'保持水平,此时弹簧测力计的读数为F0。
②拉动弹簧测力计缓慢上升(保持O点位置不变),在此过程中弹簧测力计的读数为F,利用刻度尺分别测出A、B两点上升的高度为h1、h2,请回答以下问题:
(1)在实验步骤①中,杠杆保持水平平衡,F0×OB=G×___________。
(2)在实验步骤②中,杠杆机械效率的表达式为η=___________。(用题中已知或测量的物理量符号表示)
(3)本次实验中,若提升的钩码重一定,则影响杠杆机械效率的主要因素是_________________。
(4)若只将钩码的悬挂点由A移至C,O、B位置不变,仍将钩码提升相同的高度,则杠杆的机械效率将______(选填“变大”、“变小”或“不变”)。
10.丽丽用一个高度可调节的斜面来探究斜面的省力情况、斜面的机械效率与斜面的倾斜程度之间的关系,如下图所示。她首先测出小车重,然后用弹簧测力计沿斜面拉动小车,调节斜面倾斜角θ的大小多次测量,得到下表所示的数据:
斜面
倾斜角θ
小车重G/N
斜面高
h/m
斜面长
S/m
拉力
F/N
有用功
W有/J
总功
W总/J
机械效率η
12°
5
0.2
1
2.1
1
2.1
48%
30°
5
0.5
1
3.6
2.5
3.6
69%
45°
5
0.7
1
4.3
3.5
4.3
(1) 请你替丽丽在上表中的空格处填上适当的数据______。
(2) 分析上表中的数据,可以得出的探究结论是:斜面倾斜角θ越_______,斜面越省力,斜面的机械效率越_______。
(3) 实验过程中拉力的方向应与斜面__________。
(4) 若想探究斜面的机械效率与物重的关系,则要保持__________不变,斜面的光滑程度不变,,这种研究问题的方法我们称之为____________法。
11.小红和爸爸散步时,看见小区内的一种健身器械坐拉器,如图甲所示,为了对它进行研宄,小红简化了它的结构,画出了它的模型图,如图乙所示。她发现坐在坐拉器座椅上的人,用力向下拉动手柄A时,操作杆AB会绕着转轴O转动,连杆BD拉动杆OC绕转轴O转动,将座椅向上抬起,(g取10N/kg)
(1)小红让爸爸静止坐在坐拉器的座椅上,小红竖直向下拉动手柄,将爸爸抬起经过测量,手柄竖直向下移动30cm,座椅竖直升高9cm,用时5s
①小红利用坐拉器抬起爸爸时,以下说法正确的是____
A.可以省功
B.一定定费力
C.爸爸越重,坐拉器的机械效率越高
D.爸爸被抬得越高,坐拉蕃的机槭效率越高
②若爸爸的质量为60kg,利用坐拉器抬起爸爸的机械效率为90%,则小红抬起爸爸所做功的功率为多少____?
(2)小红想通过图乙的模型,估算自己坐在坐拉器上抬起自己的拉力。图乙中OA:OB=6:1,O′C:O’D=2:1,此时AB杆处于水平位置,BD杆垂直于杆AB和O′′C,BD杆对AB和OC杆的拉力均沿着BD,且大小相等。若手臂对手柄A的拉力方向和人的重力方向视作同一直线,物体间相互作用力的大小相等、方向相反,忽略坐拉器的自重、转动是的摩擦和座椅的尺度,若小红的质量为40kg,则此时小红让自己保持图乙的状态,需要对手柄A施加竖直向下的拉力为多大____?
参考答案
1.840 1200 70% 100% 280
【解析】
人对物体所做的有用功为:
W有=Gh=840N×1m=840J;
人对物体所做的总功:
W总=FL=400N×3m=1200J;
则机械效率:
η=×100%=×100%=70%;
额外功:
W额=W总?W有=1200J?840J=360J;
则摩擦力:
f==120N;
如果斜面摩擦不计,则斜面的机械效率为100%,并且W总=W有,即FL=Gh,则拉力:
F′= ==280N。
【点睛】
根据W有用=Gh求出有用功;根据W总=Fs求出总功;根据η=求出斜面的机械效率。如果斜面摩擦不计,则W总=W有用,即FL=Gh,由此即可求出推力。
2.1000 24 83.3 偏大
【解析】
由图可知滑轮组绳子的有效股数,根据求出货物上升的高度,根据求出拉力所做的有用功,根据求出拉力做的总功,利用求出拉力做功的功率,再利用求出滑轮组的机械效率;若保持静止读数,不用克服摩擦,所测拉力偏小,总功偏小,据此分析。
【详解】
[1]由图可知,n=2,根据可得,货物上升的高度:
,
拉力所做的有用功:
,
[2]拉力做的总功:
,
拉力做功的功率:
,
[3]滑轮组的机械效率:
;
[4]若保持静止读数,不用克服摩擦,所测拉力偏小,总功偏小,测出的机械效率偏大。
3.不变 增大 80 62.5%
【解析】
影响动能的因素为:质量、速度.而影响重力势能的因素为:质量、高度.运用公式,求出总功,再运用,可求功率.运用公式,求出有用功,再运用机械效率的公式,可求出η.
(1)将物体从斜面底端匀速拉到顶端,质量不变,速度不变,则物体的动能不变.
(2)物体沿斜面升高,质量不变,高度变大,所以其重力势能增大.
(3)图中滑轮是动滑轮,则绳端通过的距离为:
;
拉力做功为:
;
拉力的功率为:
(4)此过程的有用功为:
;
这个装置的机械效率为:
;
4.右 3 一 能从杠杆上直接读力臂 < 能 杠杆存在自重 不变
【解析】
(1)[1]实验前,由于杠杆右端偏高,所以,为了使杠杆在水平位置平衡,应将两端的平衡螺母向右调节;
(2)[2]设杠杆上一个小格长度为L,一个钩码重为G,由杠杆平衡条件知道,
4G×3L=nG×4L,
解得n=3,即应在B处挂3个钩码;
[3]力臂等于支点到力的作用线的距离,当杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂可以从杠杆标尺刻度上直接读出来,所以,第一种实验方案更方便;
[4]当杠杆在水平位置平衡时,弹簧测力计的拉力与杠杆垂直,能从杠杆上直接读力臂;
[5]因为第一方案的动力臂要大于第二种方案的动力臂,根据杠杆的平衡条件知道,在阻力和阻力臂都相同的情况下,动力臂越大的越省力,所以,F1 <F2;
(3)[6]根据题意知道,当平衡螺母遗失,粘了橡皮泥后杠杆恰好在水平位置平衡时,则说明测量前杠杆能平衡,故此装置能继续用来完成探究杠杆平衡条件的实验;
(4)[7]小刚用图d装置进行探究,发现当杠杆水平平衡时,测出的数据与小明得出的杠杆平衡条件不相符,其原因是:杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响;
[8]杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,且
W有+W额=W总,
设杠杆重心升高的距离为h,所以,
Gh2 +G杠 h=Fh1 ,
若只将测力计的悬挂点由A移至C点,钩码还升高相同的高度,杠杆上旋的角度不变,杠杆升高的距离h不变,所以,Gh2 +G杠h不变,即Fh1不变。由知道,分母不变,分子不变,所以η不变。
5.1.5 2.4 62.5% 越高 费力 无关 0.3
【解析】
(1)[1]由表格第四次实验数据得到有用功:
W有=Gh=5N×0.3m=1.5J;
[2]总功:
W总=Fs=2.4N×1m=2.4J;
[3]机械效率:
η==62.5%;
(2)[4]分析斜面效率与倾斜程度关系时,应选择斜面倾斜程度不同,其它都相同的实验分析比较。由表中实验序号为1、2、4的数据可知:在物重、斜面粗糙程度相同的情况下,斜面倾斜程度越大斜面机械效率越高;
(3)[5]由表中实验序号为1、2、4的数据可知,斜面倾斜程度越大,需要的拉力越大,即:斜面越陡越费力;
(4)[6]由表中实验序号为2、3的数据可知,斜面的机械效率与物重无关;
(5)[7]由表中实验数据可知,在第一次实验中:W总1=1.5J,拉力功率
P==0.3W。
6.定 改变力的方向 斜面 省力
【解析】
[1]旗杆顶部滑轮的轴固定不动,属于定滑轮;
[2]只能改变力的方向,而不能省力;
[3][4]盘山公路相当于斜面,斜面可以省力。
7.1.2 0.24 83.3%
【解析】
(1)[1][2]如图弹簧测力计的分度值为0.2N,示数为1.2N;测力由25.0cm上升到45.0cm,所以拉力F所做的功为:
;
(2)[3]物体的重为:
钩码由0.0cm上升到10.0cm,所以对钩码做的功为:
;
动滑轮的机械效率约为:
.
8. 竖直 66.7 1、2、3
【解析】
第一空.由前3组实验数据可知s=3h,所以滑轮组由3段绳子承担物重,因此应从动滑轮上面挂钩开始绕起,如图所示:
;
第二空.为能正确在实验中测得绳子自由端的拉力应沿竖直方向匀速拉动弹簧测力计,这样才能准确测出拉力的值;
第三空.第3次实验时滑轮组的机械效率:
;
第四空.根据题意可知,前3组数据是用同一滑轮组做的实验,且物重越大,机械效率越高,所以由表中第1、2、3组数据可知,同一滑轮组的机械效率与物重有关。
9.OA 杠杆的自重 变大
【解析】
第一空.钩码的悬挂点在A点,保持水平平衡时,由杠杠的平衡条件知道, F0×OB=G×OA;
第二空.拉动弹簧测力计缓慢上升过程中,钩码的重力做的是有用功,大小是: W有 =Gh1, 拉力做的是总功,大小是: W总 =Fh2, 所以杠杆的机械效率的表达式是:
第三空.有用功是提升钩码所做的功,额外功主要是克服杠杆重力做的功,影响机械效率的因素主要是有用功和总功所占的比例;提升的钩码重一定,重物升高的距离一定,则说明有用功一定,所以,影响杠杆机械效率的主要因素是杠杆自身的重力;
第四空.杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且 W有 +W额=W总 ; 设杠杆重心升高的距离为h,则有 Gh1 +G杠 h=Fh2 , 由于G、h1 、G杠 都不变,当钩码从A点到C点时,钩码还升高相同的高度,杠杆上旋的角度减小,杠杆升高的距离h变小,则Gh1 +G杠 h变小,所以Fh2 也变小;由知道,杠杆的机械效率变大。
10.81% 小 低 平行 倾斜程度与光滑程度 控制变量
【解析】
(1)=3.5J;=4.3J;η=×100%=×100%=81%.
(2)分析表中的相关数据可以得出:物重和斜面的光滑程度相同时,斜面的倾斜角越小,机械效率越低;斜面的倾斜角越小,越省力。
(3)拉力要克服摩擦力做功,摩擦力方向沿斜面向下,所以拉力方向必须平行斜面,拉力的方向与摩擦力的方向保持在同一条直线上;
(4)若想探究斜面的机械效率与物重的关系,必须控制其它因素不变,只改变物体的重力。本题中根据实验要求,应保持斜面的倾斜角、光滑程度均不变。这里用到的研究方法是控制变量法。
11.(1)①C; ②12W; (2)100N。
【解析】
(1)使用任何机械都不能省功;费力的机械一定省距离;根据机械效率的定义和影响其大小的因素即可判断; 先求出爸爸的体重,然后根据W=Gh求出有用功,再利用效率的公式求出小红抬起爸爸所做的总功,最后根据功率的公式求出小红抬起爸爸所做功的功率: (2)根据杠杆平衡条件得,对于杠杆AOB来说有:FA×OA=FB×OB,对于杠杆O′CD来说有:(G′-FA′)×O′C=FD×O′D,结合题意二者联立即可得出答案。
【详解】
(1)①A、根据功的原理可知,使用任何机械都不能省功,故A错误; B、由题意知,当手柄竖直向下移动30cm,座椅竖直升高9cm,该装置费距离,一定省力,故B错误; C、爸爸越重,有用功占总功的比值越大,则坐拉器的机械效率越高,故C正确; D、手柄竖直向下移动30cm,座椅竖直升高9cm,即二者的比值不变,根据知,坐拉器的机械效率与爸爸的被抬的高度无关,故D错误。
②爸爸的体重:G=mg=60kg×10N/kg=600N,有用功:W有=Gh=600N×0.09m=54J,
小红抬起爸爸所做的总功:,
则小红抬起爸爸所做功的功率:;
(3)小红的重力G′=mg=40kg×10N/kg=400N,
由杠杆平衡条件得,对于杠杆AOB来说:FA×OA=FB×OB,即:---①
对于杠杆O′CD来说有:(G′-FA′)×O′C=FD×O′D,即:---②
由题意知,FB=FD,由于物体间相互作用力的大小相等,即FA=FA′,由①和②得,解得:FA=100N。
