人教版七年级下数学6.1平方根课件(29张)
文档属性
| 名称 | 人教版七年级下数学6.1平方根课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
—人人学有价值的数学; —人人都能获得必需的数学; —不同的人在数学上得到不同发展;
6.1 平方根
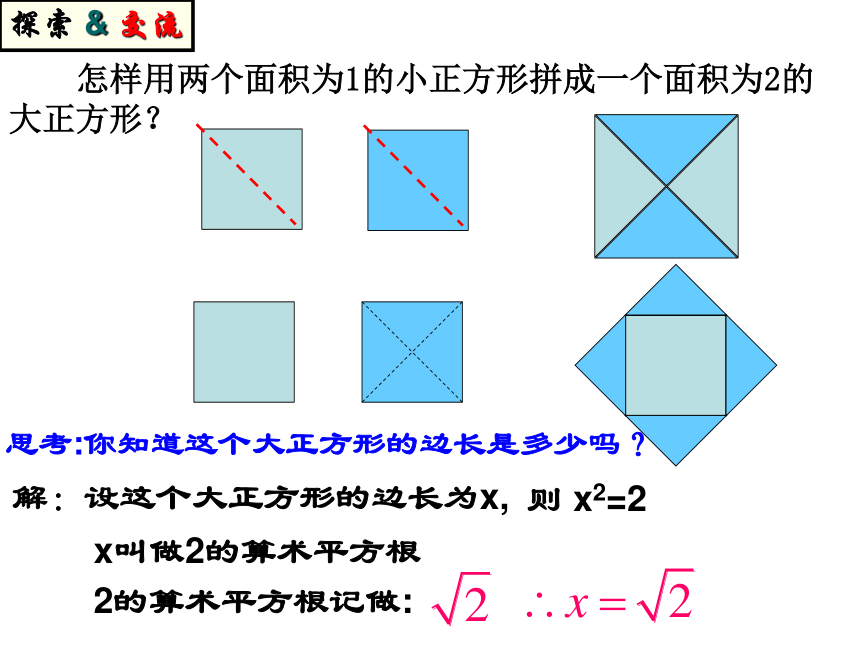
思考:你知道这个大正方形的边长是多少吗?
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
探索 & 交流
解:设这个大正方形的边长为x,
则 x2=2
x叫做2的算术平方根
2的算术平方根记做:
(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .
1.下列式子表示什么含义?你能求出它们的值吗?
规定:0的算术平方根是0.
一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为
读作: “根号a”,a 叫做被开方数.
1.双重非负性:
2.一个非负数的算数平方根的平方是它本身:
3.任何一个数的平方的算术平方根等于这个数的绝对值.
问题1、是否所有的的算术平方根都
是正数?
那么我这句话怎么改就正确了
规律一:所有的算术平方根
都是非负数
问题2、是否所有的有理数都有算术
平方根?
规律二、只有非负数才有算术平方根
问题3、被开方数都是什么数?
规律三、被开方数要求必须为非负数。
你能举出几个平方根的例子吗?
1
4
16
9
36
25
49
64
81
100
121
169
196
225
256
289
324
361
400
144
3. (1) 3的算术平方根是___.
⑶___ 算术平方根等于它本身.
3
0和1
4
6
4.已知 与 互为相反
数,求xy的算术平方根.
5.如果一个正数的算术平方根为m,则比这个数大
2的数的算术平方根是____________
判断:
(1)5是25的算术平方根; ( )
(2)-6是 36 的算术平方根; ( )
(3)0的算术平方根是0; ( )
(4)0.01是0.1的算术平方根; ( )
(5)-5是-25的算术平方根; ( )
(6)5的算术平方根是 。 ( )
筛一筛,长能耐
√
×
√
√
×
×
(1)你能否利用此折出面积为1的小正方形?
(2)你能折出面积为2的小正方形吗?
(3)折出面积为2的小正方形的边长为多少?
有多大?
<
<
因为
所以
因为
所以
… …
逼近法
无限不循环小数!
规定:0的算术平方根是0.
一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为
读作: “根号a”,a 叫做被开方数.
1.双重非负性:
2.一个非负数的算数平方根的平方是它本身:
3.任何一个数的平方的算术平方根等于这个数的绝对值.
如果一个数的平方等于9,这个数是几?
一个数的平方等于2呢?
想知道这个数的结果吗?
我们来学习——平方根
一般地,如果一个数x的平方等于a,
那么这个数叫做a的平方根或二次方根。
求一个数a的平方根的运算,叫做开平方。
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
±6
3
±2
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
a的一个平方根是3,则另一个平方根是 ,a= 。
-3
9
3a-22和2a-3是m的两个平方根,
试求m的值。
探究:
4或-2
a≤2
X≤0
补充练习;
2
13
256
≥0
-5
互为相反数
思考:
我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。
例:估计大小
小数部分=原数-整数部分
练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?
—人人学有价值的数学; —人人都能获得必需的数学; —不同的人在数学上得到不同发展;
6.1 平方根
思考:你知道这个大正方形的边长是多少吗?
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
探索 & 交流
解:设这个大正方形的边长为x,
则 x2=2
x叫做2的算术平方根
2的算术平方根记做:
(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .
1.下列式子表示什么含义?你能求出它们的值吗?
规定:0的算术平方根是0.
一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为
读作: “根号a”,a 叫做被开方数.
1.双重非负性:
2.一个非负数的算数平方根的平方是它本身:
3.任何一个数的平方的算术平方根等于这个数的绝对值.
问题1、是否所有的的算术平方根都
是正数?
那么我这句话怎么改就正确了
规律一:所有的算术平方根
都是非负数
问题2、是否所有的有理数都有算术
平方根?
规律二、只有非负数才有算术平方根
问题3、被开方数都是什么数?
规律三、被开方数要求必须为非负数。
你能举出几个平方根的例子吗?
1
4
16
9
36
25
49
64
81
100
121
169
196
225
256
289
324
361
400
144
3. (1) 3的算术平方根是___.
⑶___ 算术平方根等于它本身.
3
0和1
4
6
4.已知 与 互为相反
数,求xy的算术平方根.
5.如果一个正数的算术平方根为m,则比这个数大
2的数的算术平方根是____________
判断:
(1)5是25的算术平方根; ( )
(2)-6是 36 的算术平方根; ( )
(3)0的算术平方根是0; ( )
(4)0.01是0.1的算术平方根; ( )
(5)-5是-25的算术平方根; ( )
(6)5的算术平方根是 。 ( )
筛一筛,长能耐
√
×
√
√
×
×
(1)你能否利用此折出面积为1的小正方形?
(2)你能折出面积为2的小正方形吗?
(3)折出面积为2的小正方形的边长为多少?
有多大?
<
<
因为
所以
因为
所以
… …
逼近法
无限不循环小数!
规定:0的算术平方根是0.
一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为
读作: “根号a”,a 叫做被开方数.
1.双重非负性:
2.一个非负数的算数平方根的平方是它本身:
3.任何一个数的平方的算术平方根等于这个数的绝对值.
如果一个数的平方等于9,这个数是几?
一个数的平方等于2呢?
想知道这个数的结果吗?
我们来学习——平方根
一般地,如果一个数x的平方等于a,
那么这个数叫做a的平方根或二次方根。
求一个数a的平方根的运算,叫做开平方。
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
±6
3
±2
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
a的一个平方根是3,则另一个平方根是 ,a= 。
-3
9
3a-22和2a-3是m的两个平方根,
试求m的值。
探究:
4或-2
a≤2
X≤0
补充练习;
2
13
256
≥0
-5
互为相反数
思考:
我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。
例:估计大小
小数部分=原数-整数部分
练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?
