北师大版八年级数学下册2.5.2 一元一次不等式与一次函数课件 (共17张PPT)
文档属性
| 名称 | 北师大版八年级数学下册2.5.2 一元一次不等式与一次函数课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
初中数学八年级(下)
2.5 一元一次不等式与一次函数(第2课时)
【数学建模】
数学建模就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。
“人们对于数学产生枯燥无味、神秘难懂的印象,原因之一便是脱离实际。”
——华罗庚
【数形结合】
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休。”“数”与“形”反映了事物两个方面的属性。我们认为,数形结合,主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的。
一次函数
一元一次不等式
做一做
某电信公司有甲、乙两种手机收费业务。甲种业务规定月租费10元,每通话1min收费0.3元;乙种业务不收月租费,但每通话1min收费0.4元。你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
1、”合算”怎么理解?
思考:
2、可以用哪些学过的知识解决这个问题?
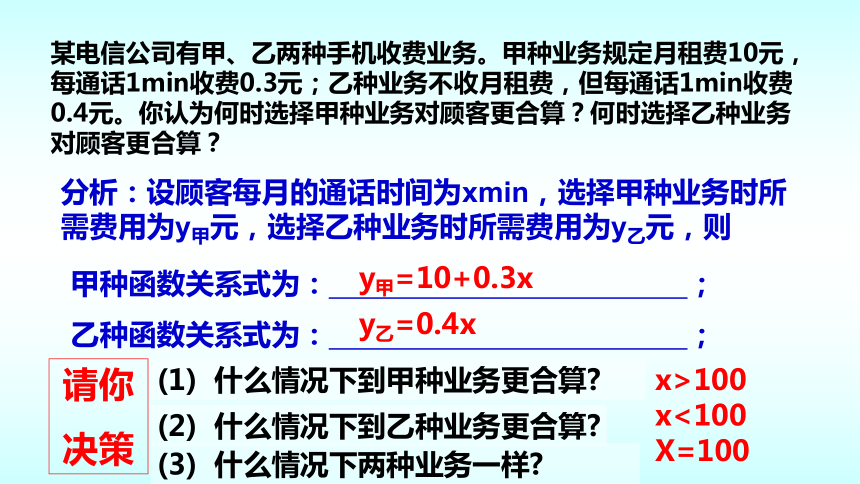
某电信公司有甲、乙两种手机收费业务。甲种业务规定月租费10元,每通话1min收费0.3元;乙种业务不收月租费,但每通话1min收费0.4元。你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
甲种函数关系式为: ;
分析:设顾客每月的通话时间为xmin,选择甲种业务时所需费用为y甲元,选择乙种业务时所需费用为y乙元,则
乙种函数关系式为: ;
y甲=10+0.3x
y乙=0.4x
请你
决策
(1) 什么情况下到甲种业务更合算?
(2) 什么情况下到乙种业务更合算?
(3) 什么情况下两种业务一样?
x>100
x<100
X=100
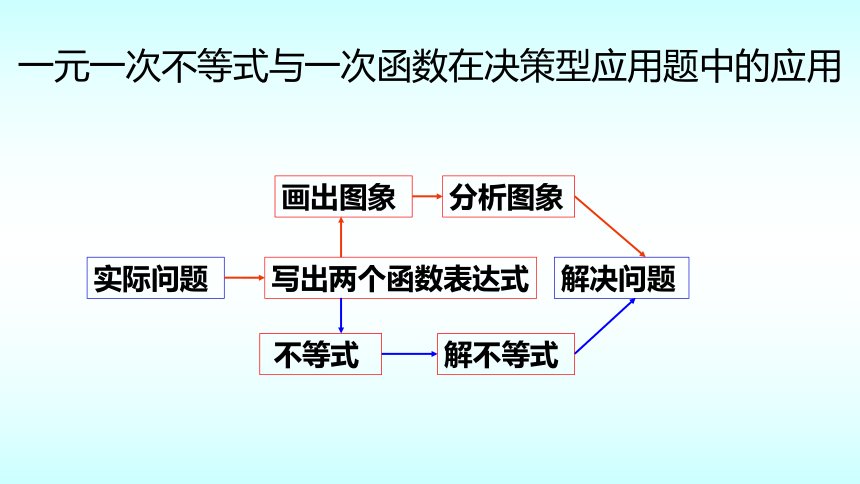
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
例题1:某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可以给予每位游客七五折优惠;乙旅行社表示可以先免去一位游客的旅游费用,其余的游客八折优惠。该单位选择哪一家旅行社支付的旅游费用较少?
“10~25人”的含义是什么?
思考:
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,则:
y1 = 200×0.75x, 即y1 = 150x
y2 = 200×0.8(x-1), 即y2= 160x-160
由y1 = y2,,得150x=160x-160,解得x=16
由y1 > y2,,得150x>160x-160,解得x<16
由y1 < y2,,得150x<160x-160,解得x>16
因为参加旅游的人数为10至25人,所以,当x=16时,甲、乙两家旅行社的收费相同;当17≤x≤25时,选择甲旅行社费用较少;当10≤x≤15时,选择乙旅行社费用较少。
应如何回答?
某公司40名员工到一景点集体参观,景点票价1元/人。该景点规定满40人可以购买团体票,票价打八折。这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠。请你帮助他们选择购票方案。
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,,得0.5x+40-x=40×0.8,解得x=16
由y1 > y2,,得0.5x+40-x>40×0.8 ,解得x<16
由y1 < y2,,得0.5x+40-x<40×0.8 ,解得x>16
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算。
一.思维主线(数形结合思想与数学建模核心素养)
实际问题——建立模型——图象和函数分析——解决问题
二.本节重点
1、掌握一元一次不等式与一次函数的关系,会运用不等式解决函数有关问题.
2、通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系.
3、感知不等式、函数、方程的不同作用与内在联系,并渗透“数形结合”思想.
4、训练大家能利用数学知识去解决问题的能力.
5、体验数、图形是有效地描述现实世界的重要手段.
整 体 建 构
作 业
P53,习题 2.7
某单位要制作一批宣传材料。甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费。
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
(1)当制作材料超过300份时,选择甲公司比较合算;
(2)当制作材料少于300份时,选择乙公司比较合算;
(3)当制作材料为300份时,两公司收费相同。
某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠。甲商场的优惠条件是:第一台按原报价收费,其余每台优惠25%。乙商场的优惠条件是:每台优惠20%。
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
(1)当买电脑超过5台时,甲商场购买更优惠
(2)当买电脑少于5台时,甲商场购买更优惠
(3)当买电脑5台时,甲商场购买更优惠
某乳品公司向某地运输一批牛奶,由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,运完这批牛奶还需其他费用600元。
(1)设该公司运输的这批牛奶为xkg,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1,y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500kg牛奶,则选用哪种运输方式所需费用较少?
(2)公路运输运送的牛奶多;铁路运费较少。
初中数学八年级(下)
2.5 一元一次不等式与一次函数(第2课时)
【数学建模】
数学建模就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。
“人们对于数学产生枯燥无味、神秘难懂的印象,原因之一便是脱离实际。”
——华罗庚
【数形结合】
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休。”“数”与“形”反映了事物两个方面的属性。我们认为,数形结合,主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的。
一次函数
一元一次不等式
做一做
某电信公司有甲、乙两种手机收费业务。甲种业务规定月租费10元,每通话1min收费0.3元;乙种业务不收月租费,但每通话1min收费0.4元。你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
1、”合算”怎么理解?
思考:
2、可以用哪些学过的知识解决这个问题?
某电信公司有甲、乙两种手机收费业务。甲种业务规定月租费10元,每通话1min收费0.3元;乙种业务不收月租费,但每通话1min收费0.4元。你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
甲种函数关系式为: ;
分析:设顾客每月的通话时间为xmin,选择甲种业务时所需费用为y甲元,选择乙种业务时所需费用为y乙元,则
乙种函数关系式为: ;
y甲=10+0.3x
y乙=0.4x
请你
决策
(1) 什么情况下到甲种业务更合算?
(2) 什么情况下到乙种业务更合算?
(3) 什么情况下两种业务一样?
x>100
x<100
X=100
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
例题1:某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可以给予每位游客七五折优惠;乙旅行社表示可以先免去一位游客的旅游费用,其余的游客八折优惠。该单位选择哪一家旅行社支付的旅游费用较少?
“10~25人”的含义是什么?
思考:
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,则:
y1 = 200×0.75x, 即y1 = 150x
y2 = 200×0.8(x-1), 即y2= 160x-160
由y1 = y2,,得150x=160x-160,解得x=16
由y1 > y2,,得150x>160x-160,解得x<16
由y1 < y2,,得150x<160x-160,解得x>16
因为参加旅游的人数为10至25人,所以,当x=16时,甲、乙两家旅行社的收费相同;当17≤x≤25时,选择甲旅行社费用较少;当10≤x≤15时,选择乙旅行社费用较少。
应如何回答?
某公司40名员工到一景点集体参观,景点票价1元/人。该景点规定满40人可以购买团体票,票价打八折。这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠。请你帮助他们选择购票方案。
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,,得0.5x+40-x=40×0.8,解得x=16
由y1 > y2,,得0.5x+40-x>40×0.8 ,解得x<16
由y1 < y2,,得0.5x+40-x<40×0.8 ,解得x>16
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算。
一.思维主线(数形结合思想与数学建模核心素养)
实际问题——建立模型——图象和函数分析——解决问题
二.本节重点
1、掌握一元一次不等式与一次函数的关系,会运用不等式解决函数有关问题.
2、通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系.
3、感知不等式、函数、方程的不同作用与内在联系,并渗透“数形结合”思想.
4、训练大家能利用数学知识去解决问题的能力.
5、体验数、图形是有效地描述现实世界的重要手段.
整 体 建 构
作 业
P53,习题 2.7
某单位要制作一批宣传材料。甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费。
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
(1)当制作材料超过300份时,选择甲公司比较合算;
(2)当制作材料少于300份时,选择乙公司比较合算;
(3)当制作材料为300份时,两公司收费相同。
某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠。甲商场的优惠条件是:第一台按原报价收费,其余每台优惠25%。乙商场的优惠条件是:每台优惠20%。
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
(1)当买电脑超过5台时,甲商场购买更优惠
(2)当买电脑少于5台时,甲商场购买更优惠
(3)当买电脑5台时,甲商场购买更优惠
某乳品公司向某地运输一批牛奶,由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,运完这批牛奶还需其他费用600元。
(1)设该公司运输的这批牛奶为xkg,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1,y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500kg牛奶,则选用哪种运输方式所需费用较少?
(2)公路运输运送的牛奶多;铁路运费较少。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
