2020年江苏数学高考模考试题中精彩解几题赏析课件(共44张PPT)
文档属性
| 名称 | 2020年江苏数学高考模考试题中精彩解几题赏析课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览






文档简介
(共44张PPT)
2020数学高考模考试题中精彩解几题赏析
图形特点
图形静止
图形特点
基本量计算——静中求值
最值与范围——动中求最
图形运动
确定性问题——动中求定
01
初读试题
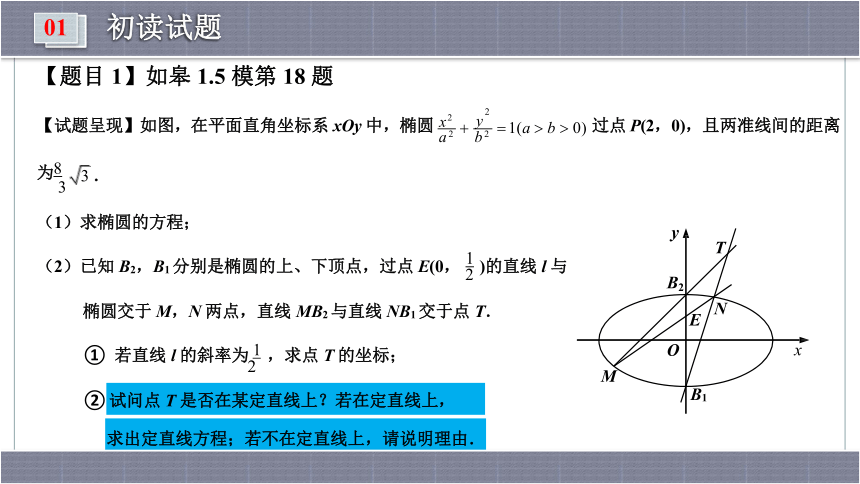
【题目 1】如皋 1.5 模第 18 题
【试题呈现】如图,在平面直角坐标系 xOy 中,椭圆 x2
a2 b2
2
? y ? 1(a ? b ? 0)
过点 P(2,0),且两准线间的距离
为 8
3
3 .
(1)求椭圆的方程;
1
(2)已知 B2,B1 分别是椭圆的上、下顶点,过点 E(0, 2 )的直线 l 与
椭圆交于 M,N 两点,直线 MB2 与直线 NB1 交于点 T.
2
① 若直线 l 的斜率为 1 ,求点 T 的坐标;
②
试问点 T 是否在某定直线上?若在定直线上,
求出定直线方程;若不在定直线上,请说明理由.
B1
M
O
x
y
T
E
N
B
2
B1
M
O
x
y
T
E
N
B2
【构图方式 3】直线 B2M 与椭圆交于 M,直线 B1N 与椭圆
交于 N,且 M,E,N 三点共线,直线 B2M 与直线 B1N 交于点 T.
解法赏析
02
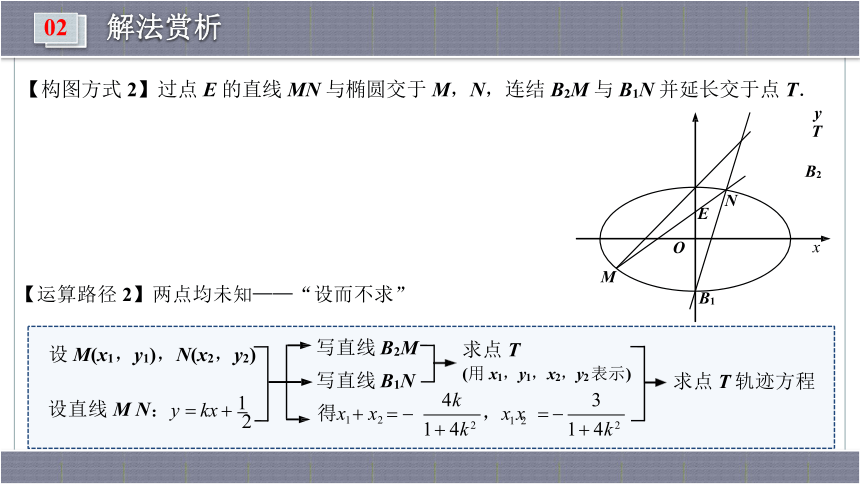
【构图方式 2】过点 E 的直线 MN 与椭圆交于 M,N,
连结 B2M 与 B1N 并延长交于点 T.
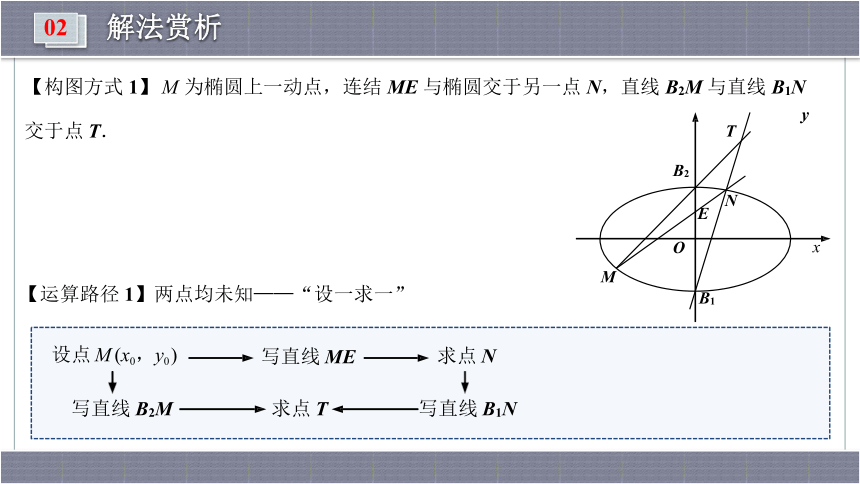
【构图方式 1】 M 为椭圆上一动点,连结 ME 与椭圆交于另一点 N,直线 B2M 与直线 B1N
交于点 T.
【构图方式 4】由点 B2 作两条动直线 B2M 和 B2N,分别交椭圆于 M 和 N,直线 MN 经过
定点 E,连结 B1N 交直线 B2M 于点 T.
B1
M
O
x
T
E
N
B2
【运算路径 1】两点均未知——“设一求一”
求点 N
设点 M (x0,y0 )
写直线 ME
求点 T
写直线 B2M
写直线 B1N
解法赏析
02
【构图方式 1】 M 为椭圆上一动点,连结 ME 与椭圆交于另一点 N,直线 B2M 与直线 B1N
y
交于点 T.
B1
O
x
y
T
E
N
B2
解法赏析
02
0 0
2
0
0
y
x
【运算过程 1】设点 M (x ,y ) ,则直线 B M 的方程为 y ?
?1 x ? 1 ①,
直线 ME 的方程为 y ? 2 y0 ?1 x ? 1 ,
2x0 2
0
x2
代入椭圆的方程,得 0 0 x2
x0
x2
? (2 y ?1)2
4 y ? 2
???0 x ? 3 ? 0 ,
0
2
2
0 N
3x2
所以 x x ??
x0 ? (2 y0 ?1)
,所以点 N 的坐标为
?
?
0
0
0 0
4 y ? 5 4 y
3x 5x ? 4
? 5
,
,M
1
0
0
3( y
x
故直线 B N 的方程为 y ?
?1) x ?1 ②,
由①②联立,求得 y ? 2 ,所以点T 在直线 y ? 2 上.
B1
M
O
x
E
N
【构图方式 2】过点 E 的直线 MN 与椭圆交于 M,N,连结 B2M 与 B1N 并延长交于点 T.
y
T
B2
【运算路径 2】两点均未知——“设而不求”
设 M(x1,y1),N(x2,y2)
2
设直线 M N:y ? kx ? 1
1 2
3
4k
1 ? 4k 2
1 ? 4k 2
得x1 ? x2 ? ?
,x x ? ?
求点 T
(用 x1,y1,x2,y2 表示)
求点 T 轨迹方程
写直线 B2M
写直线 B1N
解法赏析
02
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
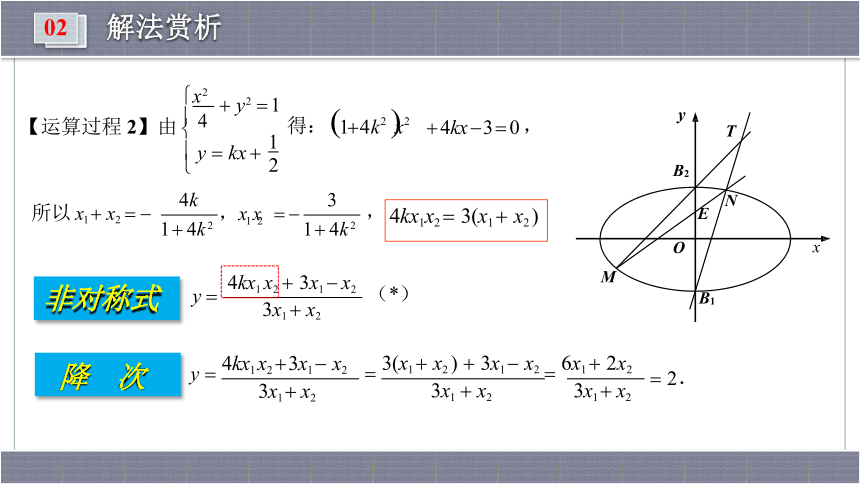
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
x1
x2
? y ? y1 ?1 x ? 1
?
由?
? y ? y2 ? 1 x ?1
??
?
得 y
?
x y ? x y ? x ? x
?
? ??x2 ? y1 ?1? ? x1 ? y2 ? 1
?
x1 y2 ? x2 y1 ? x2 ? x1
??x1 ? y2 ? 1? ? x2 ? y1 ?1???
1 2 2 1 2 1 ,
2
1 ? 2
? 2 ? 1 ?
? 2 ? 1 ?
1
2
1
2
x1 ?kx2 ?
x kx
x ? x1
?
x kx ?
x kx
? 1
2
? 1
2
? x2 ? x1
1 2 1
4kx x ? 3x ? x
?
3x1 ? x2
2 (*)
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
y ?
4kx1 x2 ? 3x1 ? x2
3x1 ? x2
(*)
y ? 4kx1 x2 ? 3x1 ? x2
3x1 ? x2
? 3(x1 ? x2 ) ? 3x1 ? x2 ? 6x1 ? 2x2 3x1 ? x2 3x1 ? x2
? 2 .
非对称式
降 次
4kx1x2 ? 3(x1 ? x2 )
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
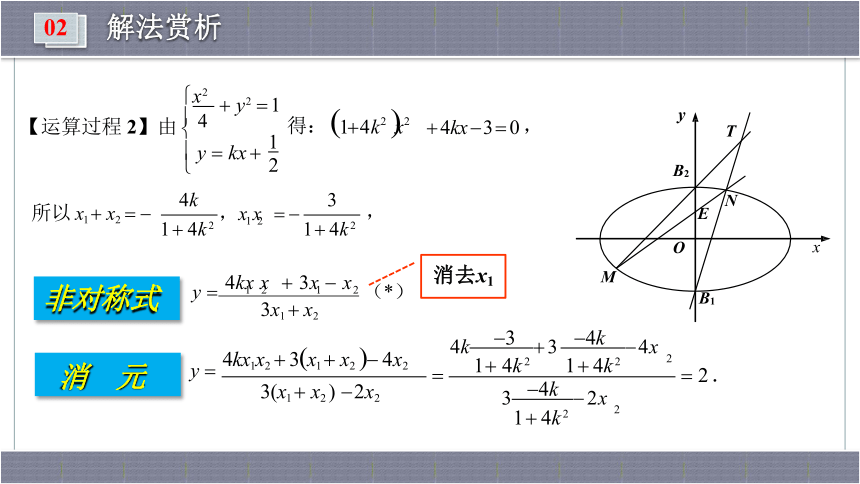
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
4kx x ? 3x ? x
3x1 ? x2
y ???1 2 1 2 (*)
2
2
4k ?3 ? 3 ?4k ? 4x
y ? 4kx1 x2 ? 3? x1 ? x2 ? ? 4x2
?
3(x1 ? x2 ) ? 2x2
1 ? 4k 2 1 ? 4k 2
3 ?4k ? 2x
1 ? 4k 2
? 2 .
非对称式
消 元
消去x1
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
4kx x ? 3x ? x
3x1 ? x2
y ???1 2 1 2 (*)
1
2x
4k ?3 ? ?4k ? 4x
1 ? 4k 2 1 ? 4k 2
y ? 4kx1 x2 ? ? x1 ? x2 ? ? 4x1 ?
2x1 ? (x1 ? x2 )
? ?4k
1 ? 4k 2
1
? 2 .
非对称式
消 元
消去x2
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
y ? 4kx1 x2 ? 3x1 ? x2
3x1 ? x2
(*)
1 2 1
2
4 x1 x2
4 ? 3 ? x1 ? x2 ? x x ? 3x ? x
3(x1 ? x2 ) ? 3x1 ? x2
y ?
?
3x1 ? x2
3x1 ? x2
? 2 .
非对称式
消 元
k ? 3 ? x1 ? x2
4 x1 x2
消去k
B1
M
O
x
T
E
N
B2
【构图方式 3】直线 B2M 与椭圆交于 M,直线 B1N 与椭圆交于 N,且 M,E,N 三点共线,
y
直线 B2M 与直线 B1N 交于点 T.
【运算路径 3】已知一交点——“知一求一”
求点 M M,E,N
求点 N 三点共线
1
设直线 B2M:y ? k x ?1
设直线 B1N:y ? k2 x ?1
求点 T(用 k1,k2 表示)
求 k1,k2 的关系
求点 T 轨迹方程
解法赏析
02
B1
M
O
x
y
T
E
N
B
2
1
? y2 ? 1
?? x2
【运算过程 3】由? 4
? y ? k x ? 1
?
得:
? ?
2 2
1
1
1? 4k x
? 8k x ? 0 ,
解法赏析
02
同理,得点 N 的坐标为
?
2
2
2 2
8k 4k 2 ?1
1 ? 4k 2 1 ? 4k 2
,
?.
1
ME
16k
12k 2 ?1
2
NE
所以直线 ME 的斜率为 k ???1 ,直线 NE 的斜率为 k
16k
4k 2 ? 3
? 2 ,
1
1
M
所以 x
?8k
?
1 ? 4k 2
,所以点 M 的坐标为
?
?
2
1
1
1
1
?8k 1 ? 4k
1 ? 4k 2
1 ? 4k 2
,
,
ME
NE
因为 M,E,N 三点共线,所以 k ? k
16k1
16k2
12k 2 ?1 4k 2 ? 3
,即 1 ? 2 ,
化简得(4k1k2 ?1)(3k1 ? k2 ) ? 0 ,又4k1k2 ?1 ? 0 ,所以 k2 ? 3k1 .
解法赏析
02
2
? y ? k x ?1
?
2 1
2k1
? y ? k x ? 1
又由 1 得: y ?
k ? k
? 1 ? 2 ,
所以点T 在直线 y ? 2 上.
B1
M
O
x
y
T
E
N
B2
1
ME
16k
12k 2 ?1
2
NE
所以直线 ME 的斜率为 k ???1 ,直线 NE 的斜率为 k
16k
4k 2 ? 3
? 2 ,
ME
NE
因为 M,E,N 三点共线,所以 k ? k
16k1 16k2
12k 2 ?1 4k 2 ? 3
,即 1 ? 2 ,
B1
M
O
x
T
E
N
B2
【运算路径 4】引入第三者——“借用结论”
证 1 设 B M:y ? kx ?1
kB2 M ? kB2 N ? ?12 2
kB N ? 3kB M 求点 T
证 1 1 2
kB1N ? kB2 N ? ? 4 设 B1N:y ? 3kx ?1
解法赏析
02
【构图方式 4】由点 B2 作两条动直线 B2M 和 B2N,分别交椭圆于 M 和 N,直线 MN 经过定点
y
E,连结 B1N 交直线 B2M 于点 T.
2
【运算过程 4】设 M(x1,y1),N(x2,y2),设直线 MN:y ? kx ? 1 ,
1
2
? x2
? y2 ? 1
由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2 ? 4kx ? 3 ? 0 ,
1 2
1 2
3
4k
所以 x ? x ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
1
2
1 2
1 2
1
2
1
2
1 2
1 2
2 2
2
12
B2 M B2 N
x
x
x x
x x
(kx ? 1)(kx ? 1)
k 2 x x ? k (x ? x ) ? 1
y ?1 y ?1
则 k ? k ?
?
?
?
4 ? ? 1 ①,
B1
M
O
x
y
T
E
N
B2
解法赏析
02
0 0
0
0
0
1
4
B1N B2 N
y2
设点 N(x ,y ) ,则k
x
x
x2
y ?1 y ?1
?1
k
? 0 ? 0 ? 0 ? ?
②,
12
B2 M B2 N
k ? k ? ? 1 ①,
解法赏析
02
0 0
0
0
0
1
4
B1N B2 N
y2
x
x
x2
y ?1 y ?1
?1
设点 N(x ,y ) ,则k ? k
? 0 ? 0 ? 0 ? ?
②,
B1
M
O
x
y
T
E
N
B
2
B1N
B2 M
①②两式相除,得k ? 3k ,
设直线 B2M 的方程为 y ? kx ?1,
则直线 B1N 的方程为 y ? 3kx ?1 ,
消去 x,求得点T 在直线 y ? 2 上.
总结提炼
03
B1
M
O
x
y
T
E
N
B2
1. 直线与椭圆相交的基本运算
已知一交点
直线与 椭圆相交
两点均未知
“知一求一”
“设而不求”
“设一求一”
“暴力求解”
2. 确定性问题的处理策略
动中求定
定点类 定值类
定轨类
直接推理 特殊先行
借用结论
背景揭示
04
y2
x2
B,右焦点为 F.设过点 T(t,m)的直线 TA,TB 与椭圆分别交于点 M (x1 ,y1 ) N(x2 ,y2 ) ,
其中 m>0,y1 ? 0,y2 ? 0 .设 t=9,求证:直线 MN 必过 x 轴上的一定点(其坐标与 m 无关).
(2010 江苏 18)在平面直角坐标系 xoy 中,如图,已知椭圆 9 + 5 ? 1 的左,右顶点为 A
M
O
x
y
T
A
N
D B
B1
M
O
x
y
T
E
N
B2
极点与极线
背景揭示
04
定义:已知圆锥曲线?:Ax2 ? Cy2 ? 2Dx ? 2Ey ? F ? 0 ,则称
点 P(x0 ,y0 ) 和直线l:Ax0 x ? Cy0 y ? D(x ? x0 ) ? E(y ? y0 ) ? F ? 0
是圆锥曲线? 的一对极点和极线.
极点与极线
P
E
F
G
H
M
N
y2
x2
a2 b2
椭圆 ?
0 0
x x y y
a2 b2
? 1 中极点 P(x ,y ) 对应的极线方程为 0 ? 0 ? 1,
m
极点Q(m ,0) 对应的极线方程为 x ? a2 .
背景揭示
04
y2
x2
a2 b2
椭圆 ?
0 0
x x y y
a2 b2
? 1 中极点 P(x ,y ) 对应的极线方程为 0 ? 0 ? 1,
m
极点Q(m ,0) 对应的极线方程为 x ? a2 .
M
O
x
y
T
N
D B
B1
M
O
E
N
y
T
B2
x2
4
x
? y2 ? 1
y2
x2
9 ? 5 ? 1
A
n
极点 R(0,n ) 对应的极线方程为 y ? b2 .
极点与极线
拓展提升
04
y2
x2
a2 b2
(1)若椭圆 E: ?
? 1(a ? b ? 0) 的左,右顶点为 A,B ,点Q(m ,t) 不在曲线 E 上,QA,
QB 分别交 E 于 C,D,直线 CD 交 x 轴于点 P(n ,0) ,则有 mn ? a2 .
x2
2
y
(2)若椭圆 E: ? 1(a ? b ? 0) 的上,下顶点为 A,B ,点Q( t ,m) 不在曲线 E 上,QA,
a2 b2
M
O
x
QB 分别交 E 于 C,D,直线 CD 交 y 轴于点 P( 0 ,n) ,则有 mn ? b2 .
y
T
A
N
D B
拓展提升
04
y2
x2
a2 b2
(3)若椭圆 E: ?
? 1(a ? b ? 0) 的左顶点为 A , P(m ,0) 为椭圆内一点,CD 为过点 P 的
一条弦,AC,AD,CD 的斜率分别为 k1,k2,k,则
① k0
k1 a ? m
? m ? a ;
1 2
a2
② k ? k
m ? a
? b2 ? m ? a ;
C
x
y
A
D
k
k1
O
2
k P
1 2
2b2
③ k(k ? k ) ? ?
a(a ? m)
;
④ k( 1 ? 1 ) ?
2a
k1 k2 a ? m
.
C
x
y
T
A
D
k1
O
k
2
0
H
k P k B
拓展提升
04
y2
x2
(4)若椭圆 E: ? ? 1(a ? b ? 0) 上一点 P(x ,y ) ,过点 P 作两条直线 PQ,PR 交椭圆
a2 b2 0 0
于 Q,R,斜率分别为 k1,k2.
1 2
a2
0
0
① k ? k ? ?(? ? b2 ) 的充要条件为直线 QR 过定点(?a2
?a2 ? b2
?a2 ? b2
? b2 x ,? ?a2
? b2 y ) ;
1 2
a2
0
x
k ? k ? b2 的充要条件为直线 QR 的斜率为? y0 ;
1 2 0
0
0 0
?
?a2
② k ? k ? ?(? ? 0) 的充要条件为直线 QR 过定点(x ? 2 y ,? 2b2 x ? y ) ;
1 2
0
b2 x
a2 y
k ? k ? 0 的充要条件为直线 QR 的斜率为 0 .
拓展提升
04
(5)A,B 是圆锥曲线上两动点,点 M 为其上一定点,MA,MB 的倾斜角分别为?,? ,
则以下条件均可得出直线 AB 过定点:
① kMAkMB ? m (常数);
② kMA ? kMB ? n (非零常数);
③ ? ? ? ? ? (0 ? ? ? π) 为定值;
④ MA ? MB 为常数.
类题展示
05
(1)求椭圆的标准方程;
(2)设直线 AC ,BD 的斜率分别为 k1,k2.
①若 k2=3k1,求证:直线 l 过定点;
②若直线 l 过椭圆的右焦点 F,试判断k1
k2
是否为定值,并说明理由.
x
x2 y2
1.(2019 通州海安上学期联考第 18 题)在平面直角坐标系 xOy 中,已知椭圆a2+b2=1
(a>b>0)的左、右顶点分别为 A、B,焦距为 2,直线 l 与椭圆交于 C,D 两点(均异于椭圆 的左、右顶点).当直线 l 过椭圆的右焦点 F 且垂直于 x 轴时,四边形 ACBD 的面积为 6.
y
A
F B
O
l C
D
k1
k
2
类题展示
05
2.(2019 如皋 2.5 模第 18 题)在平面直角坐标系 xOy 中,点 A,F 分别是椭圆 C:
x2 y2
a2 b2
F 恰为 AQ 的中点,且椭圆 C 的焦距为 2.
(1)求椭圆 C 的标准方程;
(2)过右焦点 F 的直线 l 与椭圆 C 相交于 M,N,
记直线 AM,AN 的斜率分别为 k1,k2,
若 k1+k2=-1,求直线 l 的方程.
x
? 1(a ? b ? 0) 左顶点,右焦点,椭圆 C 的右准线与 x 轴相交于点 Q,已知右焦点
y
F
A
O
l M
N
k1
k2
类题展示
05
b2
3. (2019 届百校大联考第 17 题)如图,已知椭圆 a2
x2 ? y2
6
? 1 (a>b>0)经过点( ? 2,
2
),
2
且离心率e ? 1 ,过右焦点 F 且不与坐标轴垂直的直线l 与椭圆 C 相交于 M,N 两点.
(1)求椭圆 C 的标准方程;
(2)设椭圆 C 的右顶点为 A,线段 MN 的 中点为 H,
0 1 2
记直线 OH,AM,AN 的斜率分别为k , k , k ,
k0
求证: k1 ? k2 为定值.
k1
k2
k0
类题展示
05
4. (2019 镇江一模第 18 题)已知椭圆 C:
x2 y2
a2 b2
? 1(a ? b ? 0) 的长轴长为 4,两准线间
的斜率分别为 k(k≠0),k′,求证:k·k′为定值.
距离为 4 2 .设 A 为椭圆 C 的左顶点,直线 l 过点 D(1,0),且与椭圆 C 相交于 E,F 两点.
(1)求椭圆 C 的方程;
(3)已知直线 AE,AF 分别交直线 x=3 于点 M,N,
k1
线段 MN 的中点为 Q,设直线 l 和 QD
k2
k’
k
01
初读试题
【题目 2】2019 届南京盐城二模第 18 题
y2
x2
a b
【试题呈现】在平面直角坐标系 xOy 中,已知椭圆C :
2
2
? 1(a ? b ? 0) 的离心率为 2 ,且椭圆 C 短轴
2
的一个顶点到一个焦点的距离等于 2 .
x2
2
(1)求椭圆 C 的方程; 2 +y =1.
(2)设经过点 P(2,0)的直线l 交椭圆 C 于 A,B 两点,点 Q(m,0).
①若对任意直线 l 总存在点 Q,使得 QA=QB,求实数m 的取值范围;
②设点 F 为椭圆 C 的左焦点,若点 Q 是△FAB 的外心,求实数m 的值.
B
O
x
y
Q
A
P
F
01
初读试题
(2) ①设直线的方程为 y=k(x-2),设 AB 中点为 M(x0,y0),
代入椭圆 C 的方程,消去 y,得(1+2k2)x2-8k2x+8k2-2=0.
2 2 2 2
2 2
所以△=(-8k ) -4(1+2k )( 8k -2)>0,解得- 2 <k< 2 .
8k2 8k2-2
设 A (x1,y1),B (x2,y2),则有 x1+x2=1+2k2,x1x2=1+2k2.
0
则有 x =
1 2=
x +x 4k2
0 0
2,y =k(x -2)=-
2k
2 1+2k 1+2k
2.
-
当 k≠0 时,因为 QA=QB,所以 QM⊥l,即 kQM·k=
2k
1+2k
2-0
4k2
1+2k
2-m
k=-1.解得 m=
2k2
1+2k
2.
当 k=0 时,可得 m=0,符合 m=
2k2
1+2k
2.因此 m=
2k2
1+2k
2
2.由 0≤k =
2(1-m)
m 1 1
<2,解得 0≤m<2.
P
B
O
x
因为直线 l 交椭圆 C 于两点,
y
Q
A
F
l
01
初读试题
【题目 2】2019 届南京盐城二模第 18 题
【试题呈现】在平面直角坐标系 xOy 中,已知椭圆 C:
x2
2
2 +y =1.设经过点 P(2,0)的直线l 交椭圆 C 于
P
B
O
x
A,B 两点,点 Q(m,0).设点 F 为椭圆 C 的左焦点,若点 Q 是△FAB 的外心,求实数m 的值.
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
【构图方式 1】过 A,B,F 三点作圆 Q
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
2 2 2 2
【方法一】(暴力求解)由①得(1+2k )x -8k x+8k -2
4k 2 ? 2 ? 4k 2
=0,解出以 x ?
1 ? 2k 2
1,2
,
2
2
从而得到 B(
4k 2 ? 2 ? 4k 2
?k 2 ? 4k 2 ? 2k
1 ? 2k
1 ? 2k
,
2k 2
) ,由①得Q(
1 ? 2k
,0) ,
2
2
2
2
所以由QF 2 ? QB2 ,得(
2k 2
k 2 ? 4k 2 ? 2k
?1) ? (
) ? (
1 ? 2k 2
2k 2 ? 2 ? 4k 2
1 ? 2k 2
1 ? 2k 2
) ,
化简,得(8k2 ?1)(1? 2k2 ) ? 0 ,所以 k2
1 1
=8,m=5.
圆的定义
一、从构作图形角度入手
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
【方法二】(设而不求)设 A (x1,y1),B (x2,y2),
2
1 1
由QF 2 ? QA2 得(m ?1)2 ? (m ? x )2 ? y
2
1
1
1 2
2
,又 y ? 1 ? x
,
从而得 x2 ? 4mx ? 4m ? 0 ,同理 x2 ? 4mx ? 4m ? 0 ,
1 1 2 2
所以 x1,x2 是方程 x2-4mx-4m=0 的两个根,
所以 x1+x2=4m,x1x2=-4m.
又因为 x1+x2=
1+2k
1+2k
1+2k
1+2k
1+2k
8k2 8k2-2 8k2 8k2-2 1 2k2 1
2 ,x1x2= 2 ,所以 2 =- 2 ,解得 k2=8,m= 2 =5
.
圆的定义
02
解法赏析
P
B
O
x
Q
A
F
【构图方式 1】过 A,B,F 三点作圆 Q
1 2
2 (1 ? k 2 )(2 ? 4k 2 )
【方法三】 AB ?
(x ? x )2 ? ( y ? y )2 ?
1 2 1 2
1 ? k 2 | x ? x |?
1 ? 2k 2
l
,
y
1
(1 ? k 2 )(2 ? 4k 2 )
在 Rt△AMQ 中, AM ? AB ?
2
1 ? 2k 2
,
QA ? QF ?| m ?1| ,点 Q 到 l 的距离QM ? | (m ? 2)k | ,由QA2 ? QM 2 ? AM 2 ,
1 ? k 2
2
2 2 2
(m ? 2)2 k 2 (1 ? k 2 )(2 ? 4k 2 )
得(1 ? m) ?
?
1 ? k (1 ? 2k )
,又 m=
2k2
1+2k
2
2
1
8
.解得 k = ,
1
5
m= .
圆中弦长
M
02
解法赏析
P
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
1
1
【方法四】设 A (x1,y1),B (x2,y2),则 AF 的中点为(
x ?1 y
, ) ,
2 2
圆心的确定
2
2 y1
y x ?1 x ?1
x2
? y2 ?1
x1 ? 1
B
直线 AF 的中垂线方程 y ? 1 ? ? 1 (x ? 1 ) ,令 y ? 0 ,得2x ? 1 1 ,
2
1
1
1 2
2
又 y ? 1 ? x
1
1
Q
,所以 x ?
4 x ? 1
2
1
Q
x2 x2
1 ,同理 x ?
4 x ? 1
2 ,
所以 1
1 2
x2
x2
x ? 1 x ? 1
1 2
???2 ,变形得(x x
? x1 ? x2 )(x1 ? x2 ) ? 0 ,因为 x1 ? x2 ,
1 2 1 2
所以 x x ? x ? x ? 0 ,所以
8k2
1+2k
2
?
8k2-2
1+2k
8
1 1
5
2=0,所以 k2= ,m= .
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
①由 l 与椭圆 C、l 与圆 Q 确立同解方程
【方法五】由
2
?
?
? y ? k(x ? 2),
(x ? 2) ? y2 ? (m ? 1)2,
消去 y,得?1? k2 ? x2
? (4k2 ? 2m)x ? 4k 2 ? 2m ?1 ? 0 ,
4k 2 ? 2m
所以 x1,x2 也是此方程的两个根,所以 x1 ? x2 ?
1 ? k 2
8k2
,又因为 x1+x2=1+2k2,
2
2
1 ? 2k
1 ? k
所以 , 又 m=
8k 2 ? 4k 2 ? 2m 2k2
1+2k
2
2
8
.解方程组,得 k = ,
1 1
5
m= .
02
解法赏析
P
B
O
x
y
Q
A
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
②由 l 与椭圆 C、椭圆 C 与圆 Q 确立同解方程
??(x-m)2+y2=(m+1)2,
【方法六】由?x2
2
?? 2 +y =1,
消去 y,得 x2-4mx-4m=0,F
所以 x1,x2 也是此方程的两个根,所以 x1+x2=4m,x1x2=-4m.
又因为 x1+x2=
1+2k
1+2k
2,x1x2= 2,所以
1+2k
8k2 8k2-2 8k2 8k2-2
1+2k
1
2=- 2,解得 k2=8.
所以 m=
1+2k
2k2 1
2=5.
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
③由 l 与圆 Q、椭圆 C 与圆 Q 确立同解方程
【方法七】由
2
?
?
? y ? k(x ? 2),
(x ? 2) ? y2 ? (m ? 1)2,
消去 y,
得?1? k2 ? x2
? (4k2 ? 2m)x ? 4k 2 ? 2m ?1 ? 0 ①,
?
??(x-m)2+y2=(m+1)2,
由?x2
? 2
+y2=1,
消去 y,得 x2-4mx-4m=0②,方程①②同解求得 k2
1 1
=8,m=5.
02
解法赏析
P
B
O
x
y
Q
A
F
l
二、从构作方程组角度入手
【构图方式 1】过 A,B,F 三点作圆 Q
【方法八】由题意,得 m=
2k2
1+2k
2
①,
1
2
2 y
y x ?1 x ?1
1 1
1
2
x2
? 1 ? ? 1 (m ? 1 ) ②, y ? k(x ? 2) ③, 1 ? y2 ? 1 ④,
解方程组获解.
02
解法赏析
2 2
1
2
1 1
?
? x2
? 2
【方法九】由题意,得? x2
? 2
?
? y1 ? k(x1 ? 2),
? y ? k(x ? 2),
? 1 ? y2 ? 1,
? 2 ? y2 ? 1,
?(x ? m)2 ? y2 ? 1,
??(x ? m)2 ? y2 ? 1,
2 2
解方程组获解.
二、从构作方程组角度入手
【构图方式 2】三条曲线均过点 A,B
P
B
O
x
y
Q
A
F
l
03
总结提炼
解析几何题运算求解的繁易程度受三方面影响:
构图方式
求解繁易 表达方式 消参方式
感谢聆听!欢迎指正!
“精彩试题赏析”系列
2020数学高考模考试题中精彩解几题赏析
图形特点
图形静止
图形特点
基本量计算——静中求值
最值与范围——动中求最
图形运动
确定性问题——动中求定
01
初读试题
【题目 1】如皋 1.5 模第 18 题
【试题呈现】如图,在平面直角坐标系 xOy 中,椭圆 x2
a2 b2
2
? y ? 1(a ? b ? 0)
过点 P(2,0),且两准线间的距离
为 8
3
3 .
(1)求椭圆的方程;
1
(2)已知 B2,B1 分别是椭圆的上、下顶点,过点 E(0, 2 )的直线 l 与
椭圆交于 M,N 两点,直线 MB2 与直线 NB1 交于点 T.
2
① 若直线 l 的斜率为 1 ,求点 T 的坐标;
②
试问点 T 是否在某定直线上?若在定直线上,
求出定直线方程;若不在定直线上,请说明理由.
B1
M
O
x
y
T
E
N
B
2
B1
M
O
x
y
T
E
N
B2
【构图方式 3】直线 B2M 与椭圆交于 M,直线 B1N 与椭圆
交于 N,且 M,E,N 三点共线,直线 B2M 与直线 B1N 交于点 T.
解法赏析
02
【构图方式 2】过点 E 的直线 MN 与椭圆交于 M,N,
连结 B2M 与 B1N 并延长交于点 T.
【构图方式 1】 M 为椭圆上一动点,连结 ME 与椭圆交于另一点 N,直线 B2M 与直线 B1N
交于点 T.
【构图方式 4】由点 B2 作两条动直线 B2M 和 B2N,分别交椭圆于 M 和 N,直线 MN 经过
定点 E,连结 B1N 交直线 B2M 于点 T.
B1
M
O
x
T
E
N
B2
【运算路径 1】两点均未知——“设一求一”
求点 N
设点 M (x0,y0 )
写直线 ME
求点 T
写直线 B2M
写直线 B1N
解法赏析
02
【构图方式 1】 M 为椭圆上一动点,连结 ME 与椭圆交于另一点 N,直线 B2M 与直线 B1N
y
交于点 T.
B1
O
x
y
T
E
N
B2
解法赏析
02
0 0
2
0
0
y
x
【运算过程 1】设点 M (x ,y ) ,则直线 B M 的方程为 y ?
?1 x ? 1 ①,
直线 ME 的方程为 y ? 2 y0 ?1 x ? 1 ,
2x0 2
0
x2
代入椭圆的方程,得 0 0 x2
x0
x2
? (2 y ?1)2
4 y ? 2
???0 x ? 3 ? 0 ,
0
2
2
0 N
3x2
所以 x x ??
x0 ? (2 y0 ?1)
,所以点 N 的坐标为
?
?
0
0
0 0
4 y ? 5 4 y
3x 5x ? 4
? 5
,
,M
1
0
0
3( y
x
故直线 B N 的方程为 y ?
?1) x ?1 ②,
由①②联立,求得 y ? 2 ,所以点T 在直线 y ? 2 上.
B1
M
O
x
E
N
【构图方式 2】过点 E 的直线 MN 与椭圆交于 M,N,连结 B2M 与 B1N 并延长交于点 T.
y
T
B2
【运算路径 2】两点均未知——“设而不求”
设 M(x1,y1),N(x2,y2)
2
设直线 M N:y ? kx ? 1
1 2
3
4k
1 ? 4k 2
1 ? 4k 2
得x1 ? x2 ? ?
,x x ? ?
求点 T
(用 x1,y1,x2,y2 表示)
求点 T 轨迹方程
写直线 B2M
写直线 B1N
解法赏析
02
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
x1
x2
? y ? y1 ?1 x ? 1
?
由?
? y ? y2 ? 1 x ?1
??
?
得 y
?
x y ? x y ? x ? x
?
? ??x2 ? y1 ?1? ? x1 ? y2 ? 1
?
x1 y2 ? x2 y1 ? x2 ? x1
??x1 ? y2 ? 1? ? x2 ? y1 ?1???
1 2 2 1 2 1 ,
2
1 ? 2
? 2 ? 1 ?
? 2 ? 1 ?
1
2
1
2
x1 ?kx2 ?
x kx
x ? x1
?
x kx ?
x kx
? 1
2
? 1
2
? x2 ? x1
1 2 1
4kx x ? 3x ? x
?
3x1 ? x2
2 (*)
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
y ?
4kx1 x2 ? 3x1 ? x2
3x1 ? x2
(*)
y ? 4kx1 x2 ? 3x1 ? x2
3x1 ? x2
? 3(x1 ? x2 ) ? 3x1 ? x2 ? 6x1 ? 2x2 3x1 ? x2 3x1 ? x2
? 2 .
非对称式
降 次
4kx1x2 ? 3(x1 ? x2 )
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
4kx x ? 3x ? x
3x1 ? x2
y ???1 2 1 2 (*)
2
2
4k ?3 ? 3 ?4k ? 4x
y ? 4kx1 x2 ? 3? x1 ? x2 ? ? 4x2
?
3(x1 ? x2 ) ? 2x2
1 ? 4k 2 1 ? 4k 2
3 ?4k ? 2x
1 ? 4k 2
? 2 .
非对称式
消 元
消去x1
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
4kx x ? 3x ? x
3x1 ? x2
y ???1 2 1 2 (*)
1
2x
4k ?3 ? ?4k ? 4x
1 ? 4k 2 1 ? 4k 2
y ? 4kx1 x2 ? ? x1 ? x2 ? ? 4x1 ?
2x1 ? (x1 ? x2 )
? ?4k
1 ? 4k 2
1
? 2 .
非对称式
消 元
消去x2
B1
M
O
x
y
T
E
N
B2
1
2
? x2
? y2 ? 1
【运算过程 2】由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2
? 4kx ? 3 ? 0 ,
解法赏析
02
1 2
3
4k
所以 x1 ? x2 ? ?
1 ? 4k 2 1 ? 4k 2
,x x ? ?
,
y ? 4kx1 x2 ? 3x1 ? x2
3x1 ? x2
(*)
1 2 1
2
4 x1 x2
4 ? 3 ? x1 ? x2 ? x x ? 3x ? x
3(x1 ? x2 ) ? 3x1 ? x2
y ?
?
3x1 ? x2
3x1 ? x2
? 2 .
非对称式
消 元
k ? 3 ? x1 ? x2
4 x1 x2
消去k
B1
M
O
x
T
E
N
B2
【构图方式 3】直线 B2M 与椭圆交于 M,直线 B1N 与椭圆交于 N,且 M,E,N 三点共线,
y
直线 B2M 与直线 B1N 交于点 T.
【运算路径 3】已知一交点——“知一求一”
求点 M M,E,N
求点 N 三点共线
1
设直线 B2M:y ? k x ?1
设直线 B1N:y ? k2 x ?1
求点 T(用 k1,k2 表示)
求 k1,k2 的关系
求点 T 轨迹方程
解法赏析
02
B1
M
O
x
y
T
E
N
B
2
1
? y2 ? 1
?? x2
【运算过程 3】由? 4
? y ? k x ? 1
?
得:
? ?
2 2
1
1
1? 4k x
? 8k x ? 0 ,
解法赏析
02
同理,得点 N 的坐标为
?
2
2
2 2
8k 4k 2 ?1
1 ? 4k 2 1 ? 4k 2
,
?.
1
ME
16k
12k 2 ?1
2
NE
所以直线 ME 的斜率为 k ???1 ,直线 NE 的斜率为 k
16k
4k 2 ? 3
? 2 ,
1
1
M
所以 x
?8k
?
1 ? 4k 2
,所以点 M 的坐标为
?
?
2
1
1
1
1
?8k 1 ? 4k
1 ? 4k 2
1 ? 4k 2
,
,
ME
NE
因为 M,E,N 三点共线,所以 k ? k
16k1
16k2
12k 2 ?1 4k 2 ? 3
,即 1 ? 2 ,
化简得(4k1k2 ?1)(3k1 ? k2 ) ? 0 ,又4k1k2 ?1 ? 0 ,所以 k2 ? 3k1 .
解法赏析
02
2
? y ? k x ?1
?
2 1
2k1
? y ? k x ? 1
又由 1 得: y ?
k ? k
? 1 ? 2 ,
所以点T 在直线 y ? 2 上.
B1
M
O
x
y
T
E
N
B2
1
ME
16k
12k 2 ?1
2
NE
所以直线 ME 的斜率为 k ???1 ,直线 NE 的斜率为 k
16k
4k 2 ? 3
? 2 ,
ME
NE
因为 M,E,N 三点共线,所以 k ? k
16k1 16k2
12k 2 ?1 4k 2 ? 3
,即 1 ? 2 ,
B1
M
O
x
T
E
N
B2
【运算路径 4】引入第三者——“借用结论”
证 1 设 B M:y ? kx ?1
kB2 M ? kB2 N ? ?12 2
kB N ? 3kB M 求点 T
证 1 1 2
kB1N ? kB2 N ? ? 4 设 B1N:y ? 3kx ?1
解法赏析
02
【构图方式 4】由点 B2 作两条动直线 B2M 和 B2N,分别交椭圆于 M 和 N,直线 MN 经过定点
y
E,连结 B1N 交直线 B2M 于点 T.
2
【运算过程 4】设 M(x1,y1),N(x2,y2),设直线 MN:y ? kx ? 1 ,
1
2
? x2
? y2 ? 1
由? 4
?
? y ? kx ?
?
得: ?1? 4k2 ? x2 ? 4kx ? 3 ? 0 ,
1 2
1 2
3
4k
所以 x ? x ? ?
1 ? 4k 2
1 ? 4k 2
,x x ? ?
,
1
2
1 2
1 2
1
2
1
2
1 2
1 2
2 2
2
12
B2 M B2 N
x
x
x x
x x
(kx ? 1)(kx ? 1)
k 2 x x ? k (x ? x ) ? 1
y ?1 y ?1
则 k ? k ?
?
?
?
4 ? ? 1 ①,
B1
M
O
x
y
T
E
N
B2
解法赏析
02
0 0
0
0
0
1
4
B1N B2 N
y2
设点 N(x ,y ) ,则k
x
x
x2
y ?1 y ?1
?1
k
? 0 ? 0 ? 0 ? ?
②,
12
B2 M B2 N
k ? k ? ? 1 ①,
解法赏析
02
0 0
0
0
0
1
4
B1N B2 N
y2
x
x
x2
y ?1 y ?1
?1
设点 N(x ,y ) ,则k ? k
? 0 ? 0 ? 0 ? ?
②,
B1
M
O
x
y
T
E
N
B
2
B1N
B2 M
①②两式相除,得k ? 3k ,
设直线 B2M 的方程为 y ? kx ?1,
则直线 B1N 的方程为 y ? 3kx ?1 ,
消去 x,求得点T 在直线 y ? 2 上.
总结提炼
03
B1
M
O
x
y
T
E
N
B2
1. 直线与椭圆相交的基本运算
已知一交点
直线与 椭圆相交
两点均未知
“知一求一”
“设而不求”
“设一求一”
“暴力求解”
2. 确定性问题的处理策略
动中求定
定点类 定值类
定轨类
直接推理 特殊先行
借用结论
背景揭示
04
y2
x2
B,右焦点为 F.设过点 T(t,m)的直线 TA,TB 与椭圆分别交于点 M (x1 ,y1 ) N(x2 ,y2 ) ,
其中 m>0,y1 ? 0,y2 ? 0 .设 t=9,求证:直线 MN 必过 x 轴上的一定点(其坐标与 m 无关).
(2010 江苏 18)在平面直角坐标系 xoy 中,如图,已知椭圆 9 + 5 ? 1 的左,右顶点为 A
M
O
x
y
T
A
N
D B
B1
M
O
x
y
T
E
N
B2
极点与极线
背景揭示
04
定义:已知圆锥曲线?:Ax2 ? Cy2 ? 2Dx ? 2Ey ? F ? 0 ,则称
点 P(x0 ,y0 ) 和直线l:Ax0 x ? Cy0 y ? D(x ? x0 ) ? E(y ? y0 ) ? F ? 0
是圆锥曲线? 的一对极点和极线.
极点与极线
P
E
F
G
H
M
N
y2
x2
a2 b2
椭圆 ?
0 0
x x y y
a2 b2
? 1 中极点 P(x ,y ) 对应的极线方程为 0 ? 0 ? 1,
m
极点Q(m ,0) 对应的极线方程为 x ? a2 .
背景揭示
04
y2
x2
a2 b2
椭圆 ?
0 0
x x y y
a2 b2
? 1 中极点 P(x ,y ) 对应的极线方程为 0 ? 0 ? 1,
m
极点Q(m ,0) 对应的极线方程为 x ? a2 .
M
O
x
y
T
N
D B
B1
M
O
E
N
y
T
B2
x2
4
x
? y2 ? 1
y2
x2
9 ? 5 ? 1
A
n
极点 R(0,n ) 对应的极线方程为 y ? b2 .
极点与极线
拓展提升
04
y2
x2
a2 b2
(1)若椭圆 E: ?
? 1(a ? b ? 0) 的左,右顶点为 A,B ,点Q(m ,t) 不在曲线 E 上,QA,
QB 分别交 E 于 C,D,直线 CD 交 x 轴于点 P(n ,0) ,则有 mn ? a2 .
x2
2
y
(2)若椭圆 E: ? 1(a ? b ? 0) 的上,下顶点为 A,B ,点Q( t ,m) 不在曲线 E 上,QA,
a2 b2
M
O
x
QB 分别交 E 于 C,D,直线 CD 交 y 轴于点 P( 0 ,n) ,则有 mn ? b2 .
y
T
A
N
D B
拓展提升
04
y2
x2
a2 b2
(3)若椭圆 E: ?
? 1(a ? b ? 0) 的左顶点为 A , P(m ,0) 为椭圆内一点,CD 为过点 P 的
一条弦,AC,AD,CD 的斜率分别为 k1,k2,k,则
① k0
k1 a ? m
? m ? a ;
1 2
a2
② k ? k
m ? a
? b2 ? m ? a ;
C
x
y
A
D
k
k1
O
2
k P
1 2
2b2
③ k(k ? k ) ? ?
a(a ? m)
;
④ k( 1 ? 1 ) ?
2a
k1 k2 a ? m
.
C
x
y
T
A
D
k1
O
k
2
0
H
k P k B
拓展提升
04
y2
x2
(4)若椭圆 E: ? ? 1(a ? b ? 0) 上一点 P(x ,y ) ,过点 P 作两条直线 PQ,PR 交椭圆
a2 b2 0 0
于 Q,R,斜率分别为 k1,k2.
1 2
a2
0
0
① k ? k ? ?(? ? b2 ) 的充要条件为直线 QR 过定点(?a2
?a2 ? b2
?a2 ? b2
? b2 x ,? ?a2
? b2 y ) ;
1 2
a2
0
x
k ? k ? b2 的充要条件为直线 QR 的斜率为? y0 ;
1 2 0
0
0 0
?
?a2
② k ? k ? ?(? ? 0) 的充要条件为直线 QR 过定点(x ? 2 y ,? 2b2 x ? y ) ;
1 2
0
b2 x
a2 y
k ? k ? 0 的充要条件为直线 QR 的斜率为 0 .
拓展提升
04
(5)A,B 是圆锥曲线上两动点,点 M 为其上一定点,MA,MB 的倾斜角分别为?,? ,
则以下条件均可得出直线 AB 过定点:
① kMAkMB ? m (常数);
② kMA ? kMB ? n (非零常数);
③ ? ? ? ? ? (0 ? ? ? π) 为定值;
④ MA ? MB 为常数.
类题展示
05
(1)求椭圆的标准方程;
(2)设直线 AC ,BD 的斜率分别为 k1,k2.
①若 k2=3k1,求证:直线 l 过定点;
②若直线 l 过椭圆的右焦点 F,试判断k1
k2
是否为定值,并说明理由.
x
x2 y2
1.(2019 通州海安上学期联考第 18 题)在平面直角坐标系 xOy 中,已知椭圆a2+b2=1
(a>b>0)的左、右顶点分别为 A、B,焦距为 2,直线 l 与椭圆交于 C,D 两点(均异于椭圆 的左、右顶点).当直线 l 过椭圆的右焦点 F 且垂直于 x 轴时,四边形 ACBD 的面积为 6.
y
A
F B
O
l C
D
k1
k
2
类题展示
05
2.(2019 如皋 2.5 模第 18 题)在平面直角坐标系 xOy 中,点 A,F 分别是椭圆 C:
x2 y2
a2 b2
F 恰为 AQ 的中点,且椭圆 C 的焦距为 2.
(1)求椭圆 C 的标准方程;
(2)过右焦点 F 的直线 l 与椭圆 C 相交于 M,N,
记直线 AM,AN 的斜率分别为 k1,k2,
若 k1+k2=-1,求直线 l 的方程.
x
? 1(a ? b ? 0) 左顶点,右焦点,椭圆 C 的右准线与 x 轴相交于点 Q,已知右焦点
y
F
A
O
l M
N
k1
k2
类题展示
05
b2
3. (2019 届百校大联考第 17 题)如图,已知椭圆 a2
x2 ? y2
6
? 1 (a>b>0)经过点( ? 2,
2
),
2
且离心率e ? 1 ,过右焦点 F 且不与坐标轴垂直的直线l 与椭圆 C 相交于 M,N 两点.
(1)求椭圆 C 的标准方程;
(2)设椭圆 C 的右顶点为 A,线段 MN 的 中点为 H,
0 1 2
记直线 OH,AM,AN 的斜率分别为k , k , k ,
k0
求证: k1 ? k2 为定值.
k1
k2
k0
类题展示
05
4. (2019 镇江一模第 18 题)已知椭圆 C:
x2 y2
a2 b2
? 1(a ? b ? 0) 的长轴长为 4,两准线间
的斜率分别为 k(k≠0),k′,求证:k·k′为定值.
距离为 4 2 .设 A 为椭圆 C 的左顶点,直线 l 过点 D(1,0),且与椭圆 C 相交于 E,F 两点.
(1)求椭圆 C 的方程;
(3)已知直线 AE,AF 分别交直线 x=3 于点 M,N,
k1
线段 MN 的中点为 Q,设直线 l 和 QD
k2
k’
k
01
初读试题
【题目 2】2019 届南京盐城二模第 18 题
y2
x2
a b
【试题呈现】在平面直角坐标系 xOy 中,已知椭圆C :
2
2
? 1(a ? b ? 0) 的离心率为 2 ,且椭圆 C 短轴
2
的一个顶点到一个焦点的距离等于 2 .
x2
2
(1)求椭圆 C 的方程; 2 +y =1.
(2)设经过点 P(2,0)的直线l 交椭圆 C 于 A,B 两点,点 Q(m,0).
①若对任意直线 l 总存在点 Q,使得 QA=QB,求实数m 的取值范围;
②设点 F 为椭圆 C 的左焦点,若点 Q 是△FAB 的外心,求实数m 的值.
B
O
x
y
Q
A
P
F
01
初读试题
(2) ①设直线的方程为 y=k(x-2),设 AB 中点为 M(x0,y0),
代入椭圆 C 的方程,消去 y,得(1+2k2)x2-8k2x+8k2-2=0.
2 2 2 2
2 2
所以△=(-8k ) -4(1+2k )( 8k -2)>0,解得- 2 <k< 2 .
8k2 8k2-2
设 A (x1,y1),B (x2,y2),则有 x1+x2=1+2k2,x1x2=1+2k2.
0
则有 x =
1 2=
x +x 4k2
0 0
2,y =k(x -2)=-
2k
2 1+2k 1+2k
2.
-
当 k≠0 时,因为 QA=QB,所以 QM⊥l,即 kQM·k=
2k
1+2k
2-0
4k2
1+2k
2-m
k=-1.解得 m=
2k2
1+2k
2.
当 k=0 时,可得 m=0,符合 m=
2k2
1+2k
2.因此 m=
2k2
1+2k
2
2.由 0≤k =
2(1-m)
m 1 1
<2,解得 0≤m<2.
P
B
O
x
因为直线 l 交椭圆 C 于两点,
y
Q
A
F
l
01
初读试题
【题目 2】2019 届南京盐城二模第 18 题
【试题呈现】在平面直角坐标系 xOy 中,已知椭圆 C:
x2
2
2 +y =1.设经过点 P(2,0)的直线l 交椭圆 C 于
P
B
O
x
A,B 两点,点 Q(m,0).设点 F 为椭圆 C 的左焦点,若点 Q 是△FAB 的外心,求实数m 的值.
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
【构图方式 1】过 A,B,F 三点作圆 Q
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
2 2 2 2
【方法一】(暴力求解)由①得(1+2k )x -8k x+8k -2
4k 2 ? 2 ? 4k 2
=0,解出以 x ?
1 ? 2k 2
1,2
,
2
2
从而得到 B(
4k 2 ? 2 ? 4k 2
?k 2 ? 4k 2 ? 2k
1 ? 2k
1 ? 2k
,
2k 2
) ,由①得Q(
1 ? 2k
,0) ,
2
2
2
2
所以由QF 2 ? QB2 ,得(
2k 2
k 2 ? 4k 2 ? 2k
?1) ? (
) ? (
1 ? 2k 2
2k 2 ? 2 ? 4k 2
1 ? 2k 2
1 ? 2k 2
) ,
化简,得(8k2 ?1)(1? 2k2 ) ? 0 ,所以 k2
1 1
=8,m=5.
圆的定义
一、从构作图形角度入手
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
【方法二】(设而不求)设 A (x1,y1),B (x2,y2),
2
1 1
由QF 2 ? QA2 得(m ?1)2 ? (m ? x )2 ? y
2
1
1
1 2
2
,又 y ? 1 ? x
,
从而得 x2 ? 4mx ? 4m ? 0 ,同理 x2 ? 4mx ? 4m ? 0 ,
1 1 2 2
所以 x1,x2 是方程 x2-4mx-4m=0 的两个根,
所以 x1+x2=4m,x1x2=-4m.
又因为 x1+x2=
1+2k
1+2k
1+2k
1+2k
1+2k
8k2 8k2-2 8k2 8k2-2 1 2k2 1
2 ,x1x2= 2 ,所以 2 =- 2 ,解得 k2=8,m= 2 =5
.
圆的定义
02
解法赏析
P
B
O
x
Q
A
F
【构图方式 1】过 A,B,F 三点作圆 Q
1 2
2 (1 ? k 2 )(2 ? 4k 2 )
【方法三】 AB ?
(x ? x )2 ? ( y ? y )2 ?
1 2 1 2
1 ? k 2 | x ? x |?
1 ? 2k 2
l
,
y
1
(1 ? k 2 )(2 ? 4k 2 )
在 Rt△AMQ 中, AM ? AB ?
2
1 ? 2k 2
,
QA ? QF ?| m ?1| ,点 Q 到 l 的距离QM ? | (m ? 2)k | ,由QA2 ? QM 2 ? AM 2 ,
1 ? k 2
2
2 2 2
(m ? 2)2 k 2 (1 ? k 2 )(2 ? 4k 2 )
得(1 ? m) ?
?
1 ? k (1 ? 2k )
,又 m=
2k2
1+2k
2
2
1
8
.解得 k = ,
1
5
m= .
圆中弦长
M
02
解法赏析
P
O
x
y
Q
A
F
l
【构图方式 1】过 A,B,F 三点作圆 Q
1
1
【方法四】设 A (x1,y1),B (x2,y2),则 AF 的中点为(
x ?1 y
, ) ,
2 2
圆心的确定
2
2 y1
y x ?1 x ?1
x2
? y2 ?1
x1 ? 1
B
直线 AF 的中垂线方程 y ? 1 ? ? 1 (x ? 1 ) ,令 y ? 0 ,得2x ? 1 1 ,
2
1
1
1 2
2
又 y ? 1 ? x
1
1
Q
,所以 x ?
4 x ? 1
2
1
Q
x2 x2
1 ,同理 x ?
4 x ? 1
2 ,
所以 1
1 2
x2
x2
x ? 1 x ? 1
1 2
???2 ,变形得(x x
? x1 ? x2 )(x1 ? x2 ) ? 0 ,因为 x1 ? x2 ,
1 2 1 2
所以 x x ? x ? x ? 0 ,所以
8k2
1+2k
2
?
8k2-2
1+2k
8
1 1
5
2=0,所以 k2= ,m= .
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
①由 l 与椭圆 C、l 与圆 Q 确立同解方程
【方法五】由
2
?
?
? y ? k(x ? 2),
(x ? 2) ? y2 ? (m ? 1)2,
消去 y,得?1? k2 ? x2
? (4k2 ? 2m)x ? 4k 2 ? 2m ?1 ? 0 ,
4k 2 ? 2m
所以 x1,x2 也是此方程的两个根,所以 x1 ? x2 ?
1 ? k 2
8k2
,又因为 x1+x2=1+2k2,
2
2
1 ? 2k
1 ? k
所以 , 又 m=
8k 2 ? 4k 2 ? 2m 2k2
1+2k
2
2
8
.解方程组,得 k = ,
1 1
5
m= .
02
解法赏析
P
B
O
x
y
Q
A
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
②由 l 与椭圆 C、椭圆 C 与圆 Q 确立同解方程
??(x-m)2+y2=(m+1)2,
【方法六】由?x2
2
?? 2 +y =1,
消去 y,得 x2-4mx-4m=0,F
所以 x1,x2 也是此方程的两个根,所以 x1+x2=4m,x1x2=-4m.
又因为 x1+x2=
1+2k
1+2k
2,x1x2= 2,所以
1+2k
8k2 8k2-2 8k2 8k2-2
1+2k
1
2=- 2,解得 k2=8.
所以 m=
1+2k
2k2 1
2=5.
02
解法赏析
P
B
O
x
y
Q
A
F
l
【构图方式 2】三条曲线均过点 A,B
易得圆 Q 的方程为: (x-m)2+y2=(m+1)2.
③由 l 与圆 Q、椭圆 C 与圆 Q 确立同解方程
【方法七】由
2
?
?
? y ? k(x ? 2),
(x ? 2) ? y2 ? (m ? 1)2,
消去 y,
得?1? k2 ? x2
? (4k2 ? 2m)x ? 4k 2 ? 2m ?1 ? 0 ①,
?
??(x-m)2+y2=(m+1)2,
由?x2
? 2
+y2=1,
消去 y,得 x2-4mx-4m=0②,方程①②同解求得 k2
1 1
=8,m=5.
02
解法赏析
P
B
O
x
y
Q
A
F
l
二、从构作方程组角度入手
【构图方式 1】过 A,B,F 三点作圆 Q
【方法八】由题意,得 m=
2k2
1+2k
2
①,
1
2
2 y
y x ?1 x ?1
1 1
1
2
x2
? 1 ? ? 1 (m ? 1 ) ②, y ? k(x ? 2) ③, 1 ? y2 ? 1 ④,
解方程组获解.
02
解法赏析
2 2
1
2
1 1
?
? x2
? 2
【方法九】由题意,得? x2
? 2
?
? y1 ? k(x1 ? 2),
? y ? k(x ? 2),
? 1 ? y2 ? 1,
? 2 ? y2 ? 1,
?(x ? m)2 ? y2 ? 1,
??(x ? m)2 ? y2 ? 1,
2 2
解方程组获解.
二、从构作方程组角度入手
【构图方式 2】三条曲线均过点 A,B
P
B
O
x
y
Q
A
F
l
03
总结提炼
解析几何题运算求解的繁易程度受三方面影响:
构图方式
求解繁易 表达方式 消参方式
感谢聆听!欢迎指正!
“精彩试题赏析”系列
同课章节目录
