北师大版八年级数学下册同步课件1.3.2线段的垂直平分线(20张)
文档属性
| 名称 | 北师大版八年级数学下册同步课件1.3.2线段的垂直平分线(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 08:38:24 | ||
图片预览







文档简介
课件20张PPT。第三节 线段的垂直平分线(二)第一章 三角形的证明北师大版 八年级上册一、温故知新1.线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.3.用尺规作线段的垂直平分线
已知:线段AB.求作:线段AB的垂直平分线.作法:1.分别以点A和B为圆心,以大于AB的一半长为半径画弧,两弧相交于点C和D;
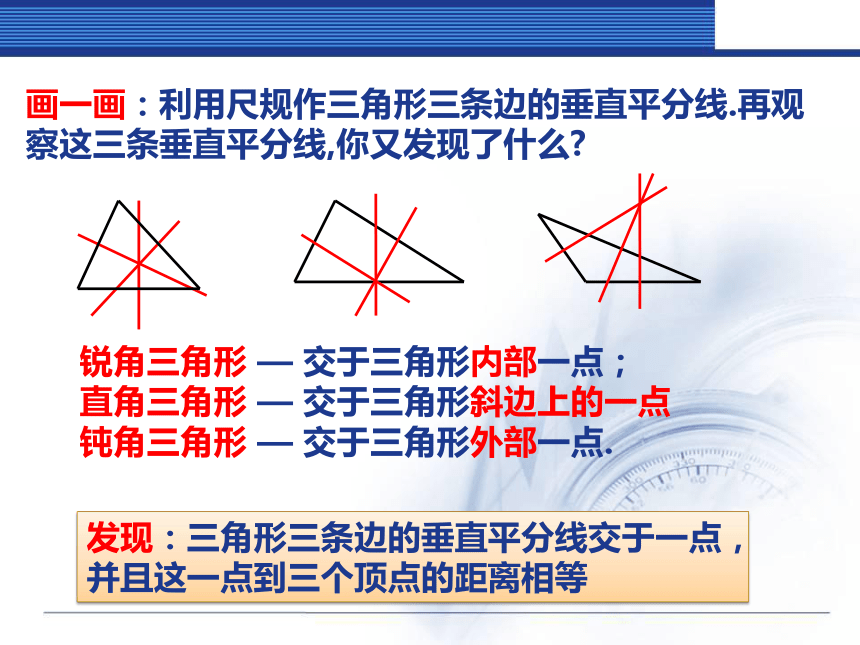
2.连接直线CD.直线CD就是线段AB的垂直平分线.操作:剪一个三角形纸片,通过折叠找出每条边的垂直平分线,观察这三条垂直平分线,你发现了什么?二、活动探究(一)发现:三角形三条边的垂直平分线交于一点,并且这一点到三个顶点的距离相等画一画:利用尺规作三角形三条边的垂直平分线.再观察这三条垂直平分线,你又发现了什么?锐角三角形 — 交于三角形内部一点;
直角三角形 — 交于三角形斜边上的一点
钝角三角形 — 交于三角形外部一点.已知:在△ABC中,边AB、BC的垂直平分线相交于点O.
求证:点O在边AC的垂直平分线上,且OA=OB=OC.证明:连接OA,OB,OC.
∵点O在线段AB的垂直平分线上,
∴OA=OB
同理OB=OC,∴OA=OC.
∴点O在线段AC的垂直平分线上
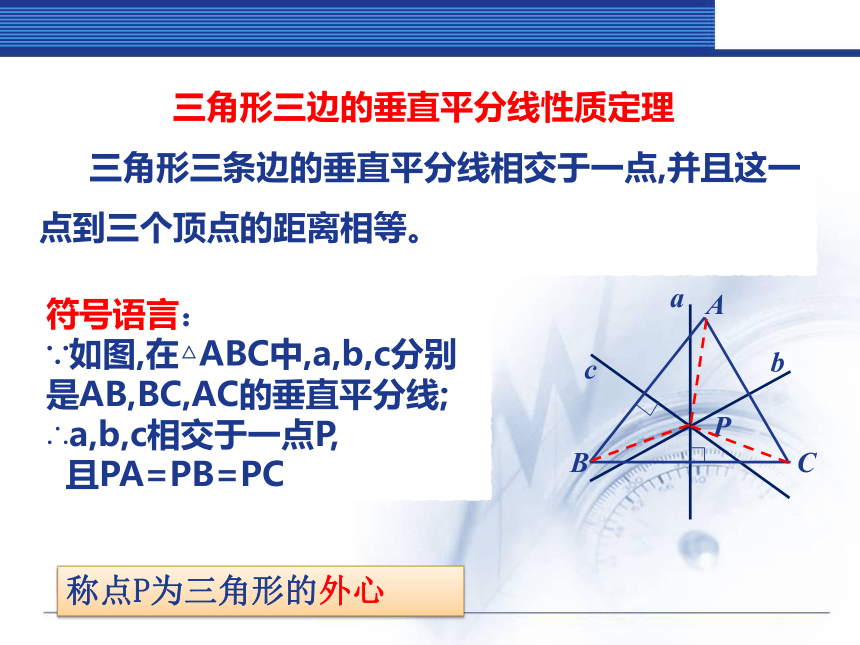
∴AB、BC、AC的垂直平分线相交于点O,且OA=OB=OC.BACO三角形三边的垂直平分线性质定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。符号语言:
∵如图,在△ABC中,a,b,c分别是AB,BC,AC的垂直平分线;
∴a,b,c相交于一点P,
且PA=PB=PC称点P为三角形的外心操作:已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能作几个?所作出的三角形都全等吗?二、活动探究(二)已知:三角形的一条边a和这条边上的高h,
求作:△ABC,使BC=a,BC边上的高为h.操作:已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能作几个?所作出的三角形都全等吗?二、活动探究(二)已知:三角形的一条边a和这条边上的高h,
求作:△ABC,使BC=a,BC边上的高为h.ah高的位置不同,所作出的三角形不都全等操作:已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?所作出的三角形都全等吗? 二、活动探究(二)这样的等腰三角形应该只有两个,分别位于底边的两侧,它们是全等的已知:线段a、h
求作:△ABC,使AB=AC,
且BC=a,高AD=hD1.作线段BC=a;2.作线段BC的垂直平分线MN交BC于D点;3.在直线MN上作线段DA,使DA=h;4.连接AB、AC.△ABC为所求的等腰三角形。作法:例:已知一个等腰三角形的底边和底边上的高,
求作这个等腰三角形。操作:
(1)已知直线l和l上一点P,利用尺规作l的垂线,使它经过点P(2)如果点P是直线l外一点,那么怎样用尺规作l的垂线,使它经过点P呢?3.作直线PC.则PC⊥直线l.情形一:点P在直线l上1.以点P为圆心,任意长为半径画弧交l于两点A和B.2.分别以点A,B为圆心,大于 AB的长为半径画弧交于点C.lABCP3.作直线PC.则PC⊥直线l.情形二:点P在直线l外1.在l的另一侧取点K,以点P为圆心,PK长为半径画弧,交l于两点A和B.2.分别以A,B为圆心,大于 AB的长为半径画弧交于点C.lABCKP三、巩固练习1.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AD
B.AB垂直平分CD
C.CD平分∠ACB
D.以上结论均不对
2.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形BC3.如图,在△ABC中,ON是AB的垂直平分线,OA=OC.
求证:点O在BC的垂直平分线4.如图,已知,在△ABC中,BC=2, ∠CAB>90°, AB的垂直平分线交BC于点E,A的垂直平分线交BC于F.
求△AEF的周长四、课堂小结1.三角形三条边的垂直平分线交于一点,且这一点到三角形三个顶点的距离相等;
2.已知等腰三角形的底边和底边上的高,用尺规作等腰三角形;用尺规过一点作已知直线的垂线.五、布置作业教材习题1.8中的第1、2、3题谢谢聆听!学习数学就像一个圆,思考的越多,半径越大,思维接触的区域就越辽阔。教师寄语
线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.3.用尺规作线段的垂直平分线
已知:线段AB.求作:线段AB的垂直平分线.作法:1.分别以点A和B为圆心,以大于AB的一半长为半径画弧,两弧相交于点C和D;
2.连接直线CD.直线CD就是线段AB的垂直平分线.操作:剪一个三角形纸片,通过折叠找出每条边的垂直平分线,观察这三条垂直平分线,你发现了什么?二、活动探究(一)发现:三角形三条边的垂直平分线交于一点,并且这一点到三个顶点的距离相等画一画:利用尺规作三角形三条边的垂直平分线.再观察这三条垂直平分线,你又发现了什么?锐角三角形 — 交于三角形内部一点;
直角三角形 — 交于三角形斜边上的一点
钝角三角形 — 交于三角形外部一点.已知:在△ABC中,边AB、BC的垂直平分线相交于点O.
求证:点O在边AC的垂直平分线上,且OA=OB=OC.证明:连接OA,OB,OC.
∵点O在线段AB的垂直平分线上,
∴OA=OB
同理OB=OC,∴OA=OC.
∴点O在线段AC的垂直平分线上
∴AB、BC、AC的垂直平分线相交于点O,且OA=OB=OC.BACO三角形三边的垂直平分线性质定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。符号语言:
∵如图,在△ABC中,a,b,c分别是AB,BC,AC的垂直平分线;
∴a,b,c相交于一点P,
且PA=PB=PC称点P为三角形的外心操作:已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能作几个?所作出的三角形都全等吗?二、活动探究(二)已知:三角形的一条边a和这条边上的高h,
求作:△ABC,使BC=a,BC边上的高为h.操作:已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能作几个?所作出的三角形都全等吗?二、活动探究(二)已知:三角形的一条边a和这条边上的高h,
求作:△ABC,使BC=a,BC边上的高为h.ah高的位置不同,所作出的三角形不都全等操作:已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?所作出的三角形都全等吗? 二、活动探究(二)这样的等腰三角形应该只有两个,分别位于底边的两侧,它们是全等的已知:线段a、h
求作:△ABC,使AB=AC,
且BC=a,高AD=hD1.作线段BC=a;2.作线段BC的垂直平分线MN交BC于D点;3.在直线MN上作线段DA,使DA=h;4.连接AB、AC.△ABC为所求的等腰三角形。作法:例:已知一个等腰三角形的底边和底边上的高,
求作这个等腰三角形。操作:
(1)已知直线l和l上一点P,利用尺规作l的垂线,使它经过点P(2)如果点P是直线l外一点,那么怎样用尺规作l的垂线,使它经过点P呢?3.作直线PC.则PC⊥直线l.情形一:点P在直线l上1.以点P为圆心,任意长为半径画弧交l于两点A和B.2.分别以点A,B为圆心,大于 AB的长为半径画弧交于点C.lABCP3.作直线PC.则PC⊥直线l.情形二:点P在直线l外1.在l的另一侧取点K,以点P为圆心,PK长为半径画弧,交l于两点A和B.2.分别以A,B为圆心,大于 AB的长为半径画弧交于点C.lABCKP三、巩固练习1.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AD
B.AB垂直平分CD
C.CD平分∠ACB
D.以上结论均不对
2.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形BC3.如图,在△ABC中,ON是AB的垂直平分线,OA=OC.
求证:点O在BC的垂直平分线4.如图,已知,在△ABC中,BC=2, ∠CAB>90°, AB的垂直平分线交BC于点E,A的垂直平分线交BC于F.
求△AEF的周长四、课堂小结1.三角形三条边的垂直平分线交于一点,且这一点到三角形三个顶点的距离相等;
2.已知等腰三角形的底边和底边上的高,用尺规作等腰三角形;用尺规过一点作已知直线的垂线.五、布置作业教材习题1.8中的第1、2、3题谢谢聆听!学习数学就像一个圆,思考的越多,半径越大,思维接触的区域就越辽阔。教师寄语
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
