初中数学中考常考几何题型必杀技---八大模型
文档属性
| 名称 | 初中数学中考常考几何题型必杀技---八大模型 |
|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览


文档简介
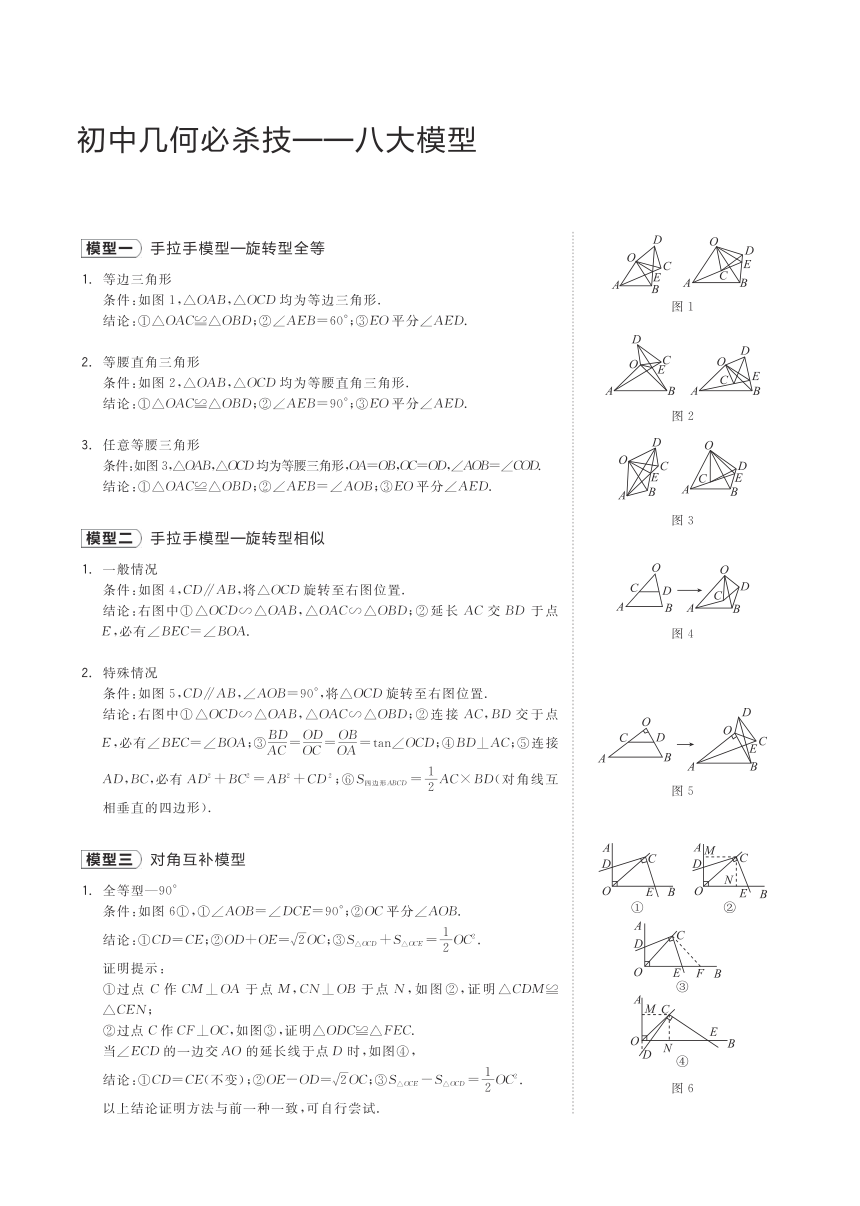
初中几何必杀技
大模型
模型一手拉手模型一旋转型全等
1.等边三角形
条件:如图1,△OAB,△OCD均为等边三角形
结论:①△OAC≌△OBD;②∠AEB=60°;③EO平分∠AED
2,
直角三角形
条件:如图2,△OAB,△OCD均为等腰直角三角形
结论:①△OAC≌△OBD;②∠AEB=90°;③EO平分∠AED
3.任意等腰三角形
条件:如图3,△OAB,△OCD均为等腰三角形,OA=OBOC=OD.∠AOB=∠COD
结论:①△OAC≌△OBD;②∠AEB=∠AOB;③EO平分∠AED.
模型二手拉手模型一旋转型相似
1.一般情况
条件:如图4,CD∥AB,将△OCD旋转至右图位置
结论:右图中①△OCD∽△OAB,△OAC∽△OBD;②延长AC交BD于点
E,必有∠BEC=∠BOA
图
2.特殊情况
条件:如图5,CD∥AB,∠AOB=90°,将△OCD旋转至右图位置
结论:右图中①△OCD∽△OAB,△OAC∽△OBD;②连接AC,BD交于点
E,必有∠BEC=∠BOA:③AC=C=OA=ta∠OCD;④BD⊥AC;⑤连接
AD,BC,必有AD2+BC=AB+CD2;⑥Sm边形MD=AC×BD(对角线互
相垂直的四边形)
模型三对角互补模型
1.全等型—90
条件:如图6①,①∠AOB=∠DCE=90°;②OC平分∠AOB
结论:①CD=CE;②OD+OE=2OC:③S△D+SxE=2OC
证明提示
①过点C作CM⊥OA于点M,CN⊥OB于点N,如图②,证明△CDM≌
△CEN;
②过点C作CF⊥OC,如图③,证明△ODC≌△FEC.
当∠ECD的一边交AO的延长线于点D时,如图④
结论:①CD=CE(不变);②OE-OD=vOC;③S△cE-Sxm=OC
以上结论证明方法与前一种一致,可自行尝试
条件:如图7①,①∠AOB=2∠DCE=120°;②OC平分∠AO
结论:①CD=CE;②OD+OE=OC;③ Sacn+S△E=OC
证明提示:
①可参考“全等型90°证明结论①;②如图②,在OB上取一点F,使OF
OC,证明△ECF≌△DCO
当∠DCE的一边交AO的延长线于点D时,如图③,结论:①CD=CE;
②OE-OD=OC;③SAa-SAa
以上结论证明方法与前一种一致
3.全等型一任意角a
条件:如图8①,①∠AOB=2a,∠DCE=180-2a;②CD=CE
结论:①OC平分∠AOB;②OD+OE=2OC·cosa;③SaD+S△g=OC
sina
当∠DCE的一边交AO的延长线于点D时(如图②)
结论:①OC平分∠AOB;②OE-OD=2OC·cosa;③S△aE-S△aD=OC
可参考上述方法进行证明
对角互补模型总结
①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边
②初始条件“角平分线”与“两边相等”的区别
③两种常见的辅助线作法
④注意OC平分∠AOB时,∠CDE=∠CED=∠COA=∠COB如何推导
模型四角含半角模型90
角含半角模型90-1
A
条件:如图10①,①正方形ABCD;②∠EAF=45
结论:①EF=DF+BE
②△CEF的周长为正方形ABCD周长的
也可以这样:
条件:①正方形ABCD;②EF=DF+BE
结论:∠EAF=45°
2.角含半角模型90-2
条件:如图11①,①正方形ABCD;②∠EAF=45
结论
辅助线如图11②所示
3.角含半角模型90°-3
条件:如图12,①R1△ABC;
②∠DAE=45°
结论:BD2+CE=DE
若∠DAE旋转到△ABC外部时,结论BD+CE=DE仍然成立
图12
大模型
模型一手拉手模型一旋转型全等
1.等边三角形
条件:如图1,△OAB,△OCD均为等边三角形
结论:①△OAC≌△OBD;②∠AEB=60°;③EO平分∠AED
2,
直角三角形
条件:如图2,△OAB,△OCD均为等腰直角三角形
结论:①△OAC≌△OBD;②∠AEB=90°;③EO平分∠AED
3.任意等腰三角形
条件:如图3,△OAB,△OCD均为等腰三角形,OA=OBOC=OD.∠AOB=∠COD
结论:①△OAC≌△OBD;②∠AEB=∠AOB;③EO平分∠AED.
模型二手拉手模型一旋转型相似
1.一般情况
条件:如图4,CD∥AB,将△OCD旋转至右图位置
结论:右图中①△OCD∽△OAB,△OAC∽△OBD;②延长AC交BD于点
E,必有∠BEC=∠BOA
图
2.特殊情况
条件:如图5,CD∥AB,∠AOB=90°,将△OCD旋转至右图位置
结论:右图中①△OCD∽△OAB,△OAC∽△OBD;②连接AC,BD交于点
E,必有∠BEC=∠BOA:③AC=C=OA=ta∠OCD;④BD⊥AC;⑤连接
AD,BC,必有AD2+BC=AB+CD2;⑥Sm边形MD=AC×BD(对角线互
相垂直的四边形)
模型三对角互补模型
1.全等型—90
条件:如图6①,①∠AOB=∠DCE=90°;②OC平分∠AOB
结论:①CD=CE;②OD+OE=2OC:③S△D+SxE=2OC
证明提示
①过点C作CM⊥OA于点M,CN⊥OB于点N,如图②,证明△CDM≌
△CEN;
②过点C作CF⊥OC,如图③,证明△ODC≌△FEC.
当∠ECD的一边交AO的延长线于点D时,如图④
结论:①CD=CE(不变);②OE-OD=vOC;③S△cE-Sxm=OC
以上结论证明方法与前一种一致,可自行尝试
条件:如图7①,①∠AOB=2∠DCE=120°;②OC平分∠AO
结论:①CD=CE;②OD+OE=OC;③ Sacn+S△E=OC
证明提示:
①可参考“全等型90°证明结论①;②如图②,在OB上取一点F,使OF
OC,证明△ECF≌△DCO
当∠DCE的一边交AO的延长线于点D时,如图③,结论:①CD=CE;
②OE-OD=OC;③SAa-SAa
以上结论证明方法与前一种一致
3.全等型一任意角a
条件:如图8①,①∠AOB=2a,∠DCE=180-2a;②CD=CE
结论:①OC平分∠AOB;②OD+OE=2OC·cosa;③SaD+S△g=OC
sina
当∠DCE的一边交AO的延长线于点D时(如图②)
结论:①OC平分∠AOB;②OE-OD=2OC·cosa;③S△aE-S△aD=OC
可参考上述方法进行证明
对角互补模型总结
①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边
②初始条件“角平分线”与“两边相等”的区别
③两种常见的辅助线作法
④注意OC平分∠AOB时,∠CDE=∠CED=∠COA=∠COB如何推导
模型四角含半角模型90
角含半角模型90-1
A
条件:如图10①,①正方形ABCD;②∠EAF=45
结论:①EF=DF+BE
②△CEF的周长为正方形ABCD周长的
也可以这样:
条件:①正方形ABCD;②EF=DF+BE
结论:∠EAF=45°
2.角含半角模型90-2
条件:如图11①,①正方形ABCD;②∠EAF=45
结论
辅助线如图11②所示
3.角含半角模型90°-3
条件:如图12,①R1△ABC;
②∠DAE=45°
结论:BD2+CE=DE
若∠DAE旋转到△ABC外部时,结论BD+CE=DE仍然成立
图12
同课章节目录
