五年级上册数学课件- 第六单元 数学百花园 复习课件|北京版 (共22张PPT)
文档属性
| 名称 | 五年级上册数学课件- 第六单元 数学百花园 复习课件|北京版 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 934.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
六 数学百花园
复习课件
数学百花园
密铺
含义
特点
应用
鸡兔同笼问题
解决方法、现代生活应用
知识框架
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片。又叫做平面图形的镶嵌。
密铺
复习旧知
平面密铺的特点
(1)用一种或几种全等图形进行拼接.
(2)拼接处不留空隙、不重叠.
(3)能连续铺成一片.
能密铺的图形在一个拼接点处的特点:
几个图形的内角拼接在一起时,其和等于360?,并使相等的边互相重合。
三角形一定可以密铺.
正六边形可以密铺.
1. 因为三角形的内角和是180°, 用几个全等三角形拼接时,每个角只需用两次,就能拼出一个周角,所以
2.任意四边形的四个内角之和是360°,而密铺时拼接点的四个角刚好能拼成一个周角,所以
任意四边形一定可以密铺.
3.正六边形的每个内角都是120°,也能拼接出周角,所以
可以用同一种正多边形密铺的图形只有正三角形,正四边形,正六边形。
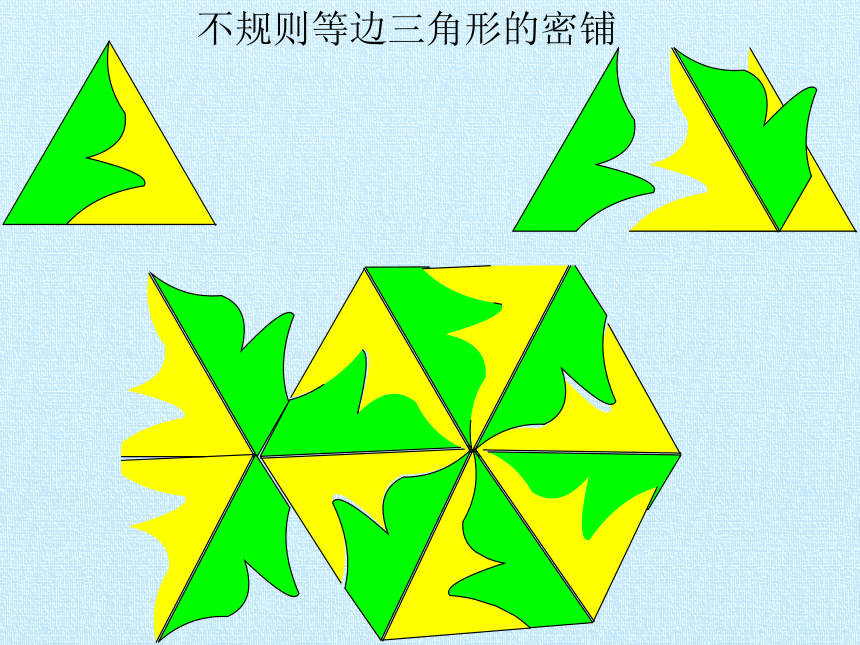
不规则等边三角形的密铺
注意:两种边长相等的正多边形也可以组合密铺。
正五边形不能单独密铺,但可以和其它图形组合密铺。
组合密铺
组合密铺
组合密铺
小结:
1.平面图形的密铺指没有空隙和不重叠的拼接;
2.用一种多边形密铺时,三角形,四边形,正六边形都能密铺。
密铺在现实生活中应用非常广泛。
复习旧知
鸡和兔分别有多少只?
我们和兔一共
有8个头。
我们和鸡一共
有26条腿
解决方法?
方法一:画图假设法。
假设全是鸡,一共8个头,
16条腿,还多出
(26-16)条腿,
即多10条腿。
把其中的鸡改成兔子,
改一只增加两条腿,
要把10条腿都分完,要
把5只鸡改成5只兔。
鸡有3只,兔有5只。
方法二:列表法。
鸡有3只,兔有5只。
鸡的只数 7 6 5 4 3 2 ……
兔的只数 1 2 3 4 5 6 ……
共有腿数 18 20 22 24 26 28 ……
方法三:古人解“鸡兔同笼”的方法。
鸡有3只,兔有5只。
26÷2=13(条)
13-8=5(只)
8-5=3(只)
假设让鸡抬起一条腿,兔子抬起
两条腿,还有(26÷2)条腿。
这时每只鸡一条腿,每只兔子两条
腿,笼子里只要有一只兔子,
则腿的总数就比头的总数多1。
这时腿的总数与头的总数之差
(13-8),也就是兔子的只数。
鸡和兔一共8只,鸡的只数=
总数-兔的只数。
鸡兔同笼问题具有独特的魅力,生活中很多事情的解决涉及这一问题。
◆自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有几辆?
鸡有2脚,怪兔有5脚,共8头,34脚。
鸡有多少只?怪兔有多少只?
◆信封里有2元和5元的钞票,共8张,34元。两种钞票各多少张?
鸡有2脚,怪兔有3脚,共10头,26脚。
鸡有多少只?怪兔有多少只?
巩固练习
1.在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形。
答案:正12边形
解析:记住要密铺的话,公共顶点内角和要为周角即360°,正方形顶角为90°,正六边形顶角为120°,所以剩下的那个角=360-90-120=1 50°,若顶角为150°,套公式,设其为正N边形,有(N-2)*180 =N*150,解得,N=12,所以要铺上一个正12边形。做这种题目,就只要记住公共顶角部分和为360°,否则不能密铺的。
2.一幅美丽的图案,在某个顶点处有四个边长相等的正多边形拼接而成,其中的3个分别是正三角形、正方形、正六边形,则另一个为_________。
答案:正四边形
解析:正三角形的一个角是60°,正四边形的一个角是90°,正六边形的一个角是( 6-2)×180°÷2=120°,360°-60°-90°-120°=90°,因此还需要一个正四边形。
3.松鼠妈妈采松子,晴天每天采20个,雨天每天可采12个,它一连采了112个,平均每天采14个,这几天中有________天是雨天。
答案:6天
解析:(112÷14×20-112)÷(20-12)=6(天)
4.某人领得工资240元,有2元,5元,10元三种人民币共50张,其中2元和5元的张数一样多,那么10元的有________张。
答案:10张
解析:(10×50-240)÷[10-(2+5)÷2]=40(张)
[240-(2+5)×(40÷2)]÷10=10(张)
六 数学百花园
复习课件
数学百花园
密铺
含义
特点
应用
鸡兔同笼问题
解决方法、现代生活应用
知识框架
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片。又叫做平面图形的镶嵌。
密铺
复习旧知
平面密铺的特点
(1)用一种或几种全等图形进行拼接.
(2)拼接处不留空隙、不重叠.
(3)能连续铺成一片.
能密铺的图形在一个拼接点处的特点:
几个图形的内角拼接在一起时,其和等于360?,并使相等的边互相重合。
三角形一定可以密铺.
正六边形可以密铺.
1. 因为三角形的内角和是180°, 用几个全等三角形拼接时,每个角只需用两次,就能拼出一个周角,所以
2.任意四边形的四个内角之和是360°,而密铺时拼接点的四个角刚好能拼成一个周角,所以
任意四边形一定可以密铺.
3.正六边形的每个内角都是120°,也能拼接出周角,所以
可以用同一种正多边形密铺的图形只有正三角形,正四边形,正六边形。
不规则等边三角形的密铺
注意:两种边长相等的正多边形也可以组合密铺。
正五边形不能单独密铺,但可以和其它图形组合密铺。
组合密铺
组合密铺
组合密铺
小结:
1.平面图形的密铺指没有空隙和不重叠的拼接;
2.用一种多边形密铺时,三角形,四边形,正六边形都能密铺。
密铺在现实生活中应用非常广泛。
复习旧知
鸡和兔分别有多少只?
我们和兔一共
有8个头。
我们和鸡一共
有26条腿
解决方法?
方法一:画图假设法。
假设全是鸡,一共8个头,
16条腿,还多出
(26-16)条腿,
即多10条腿。
把其中的鸡改成兔子,
改一只增加两条腿,
要把10条腿都分完,要
把5只鸡改成5只兔。
鸡有3只,兔有5只。
方法二:列表法。
鸡有3只,兔有5只。
鸡的只数 7 6 5 4 3 2 ……
兔的只数 1 2 3 4 5 6 ……
共有腿数 18 20 22 24 26 28 ……
方法三:古人解“鸡兔同笼”的方法。
鸡有3只,兔有5只。
26÷2=13(条)
13-8=5(只)
8-5=3(只)
假设让鸡抬起一条腿,兔子抬起
两条腿,还有(26÷2)条腿。
这时每只鸡一条腿,每只兔子两条
腿,笼子里只要有一只兔子,
则腿的总数就比头的总数多1。
这时腿的总数与头的总数之差
(13-8),也就是兔子的只数。
鸡和兔一共8只,鸡的只数=
总数-兔的只数。
鸡兔同笼问题具有独特的魅力,生活中很多事情的解决涉及这一问题。
◆自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有几辆?
鸡有2脚,怪兔有5脚,共8头,34脚。
鸡有多少只?怪兔有多少只?
◆信封里有2元和5元的钞票,共8张,34元。两种钞票各多少张?
鸡有2脚,怪兔有3脚,共10头,26脚。
鸡有多少只?怪兔有多少只?
巩固练习
1.在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形。
答案:正12边形
解析:记住要密铺的话,公共顶点内角和要为周角即360°,正方形顶角为90°,正六边形顶角为120°,所以剩下的那个角=360-90-120=1 50°,若顶角为150°,套公式,设其为正N边形,有(N-2)*180 =N*150,解得,N=12,所以要铺上一个正12边形。做这种题目,就只要记住公共顶角部分和为360°,否则不能密铺的。
2.一幅美丽的图案,在某个顶点处有四个边长相等的正多边形拼接而成,其中的3个分别是正三角形、正方形、正六边形,则另一个为_________。
答案:正四边形
解析:正三角形的一个角是60°,正四边形的一个角是90°,正六边形的一个角是( 6-2)×180°÷2=120°,360°-60°-90°-120°=90°,因此还需要一个正四边形。
3.松鼠妈妈采松子,晴天每天采20个,雨天每天可采12个,它一连采了112个,平均每天采14个,这几天中有________天是雨天。
答案:6天
解析:(112÷14×20-112)÷(20-12)=6(天)
4.某人领得工资240元,有2元,5元,10元三种人民币共50张,其中2元和5元的张数一样多,那么10元的有________张。
答案:10张
解析:(10×50-240)÷[10-(2+5)÷2]=40(张)
[240-(2+5)×(40÷2)]÷10=10(张)
