北师大版八年级数学下册3.2图形的旋转(2) 课件 (共30张PPT)
文档属性
| 名称 | 北师大版八年级数学下册3.2图形的旋转(2) 课件 (共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 18:04:26 | ||
图片预览






文档简介
(共30张PPT)
初中数学八年级(下)
3.2 图形的旋转(第2课时)
知识回顾
1、什么叫旋转?
2、旋转的基本性质是什么?
按下暂停键,自己想一想
旋转前、后的图形全等:对应线段相等,对应角相等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转的基本性质:
知识回顾
旋转定义:
在平面内,将一个图形绕定点按一定方向转动一定角度 .这样的图形运动叫做旋转,这个定点称为旋转中心,转动的角称为 旋转角 .
动手操作,自主探究
旋转画图
作 图 工 具: 刻度尺、量角器、铅笔.
基本作图技能:1.画一条线段等于已知线段;
2.画一个角等于已知角.
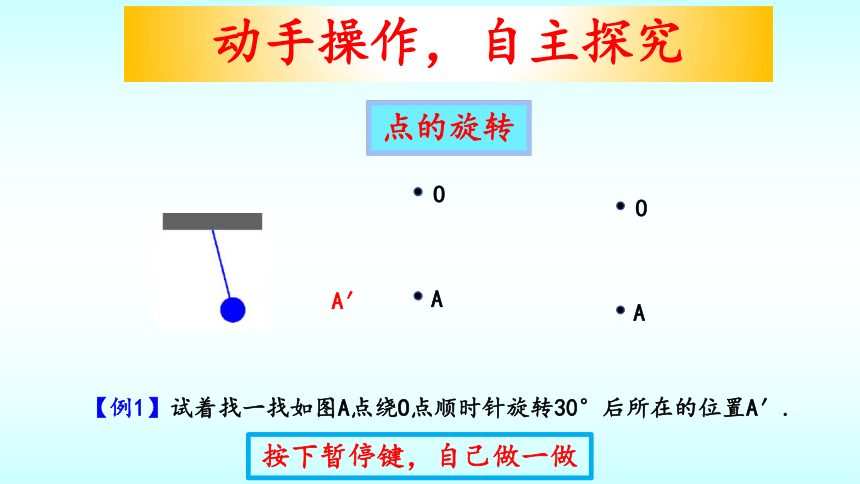
点的旋转
【例1】试着找一找如图A点绕O点顺时针旋转30°后所在的位置A′.
A
O
A′
A
O
动手操作,自主探究
按下暂停键,自己做一做
点的旋转
【例1】试着找一找如图A点绕O点顺时针旋转30°后所在的位置A′.
A
O
A′
动手操作,自主探究
解:(1)以OA为一边按顺时针方向画∠AOX,使得∠AOX=30°.
(2)在射线OX上取点A′,使得OA′=OA.
点A′就是点A绕点O按顺时针方向旋转30°后的点.
X
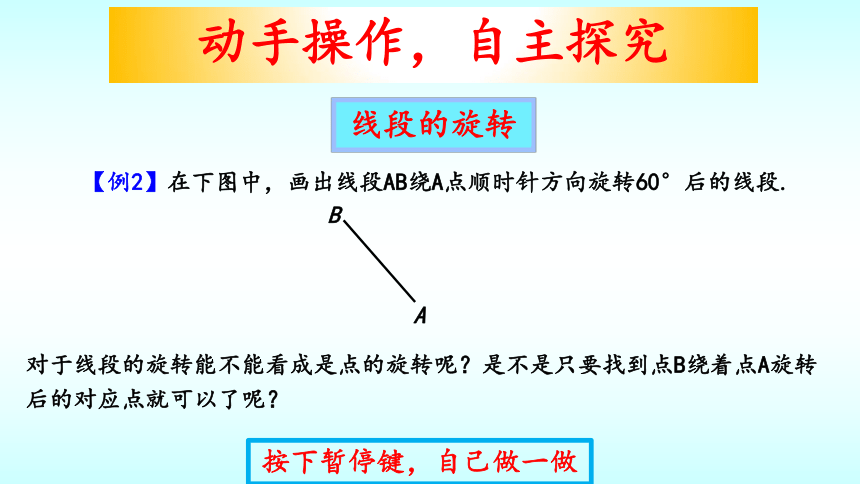
【例2】在下图中,画出线段AB绕A点顺时针方向旋转60°后的线段.
线段的旋转
B
A
对于线段的旋转能不能看成是点的旋转呢?是不是只要找到点B绕着点A旋转后的对应点就可以了呢?
动手操作,自主探究
按下暂停键,自己做一做
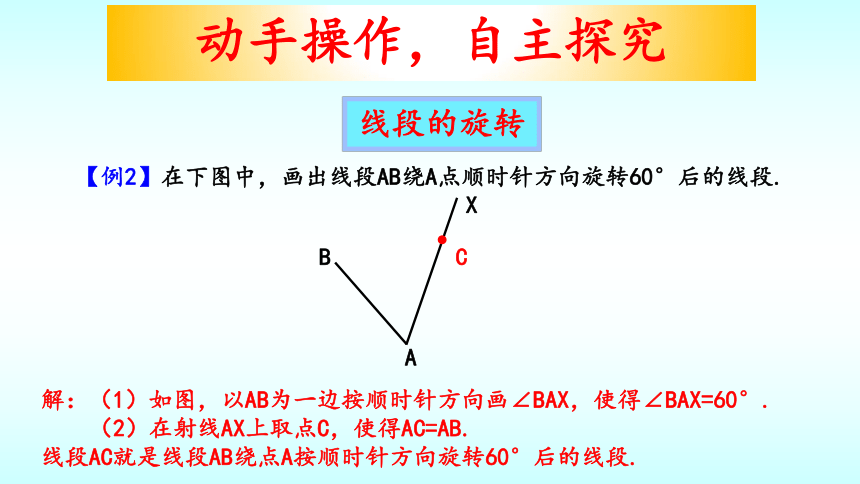
【例2】在下图中,画出线段AB绕A点顺时针方向旋转60°后的线段.
线段的旋转
解:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
B
X
C
A
动手操作,自主探究
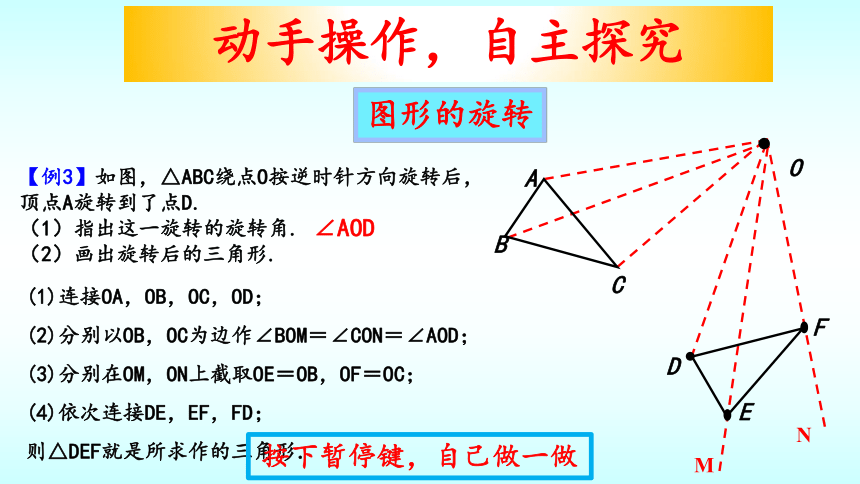
【例3】如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
图形的旋转
B
O
C
A
D
∠AOD
E
F
动手操作,自主探究
(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形.
N
M
按下暂停键,自己做一做
总结:确定一个图形旋转后的位置的条件为:
①旋转中心、②旋转方向、③旋转角度.
确定一个图形旋转后的位置,需要哪些条件?
探究总结,形成认知
按下暂停键,自己想一想
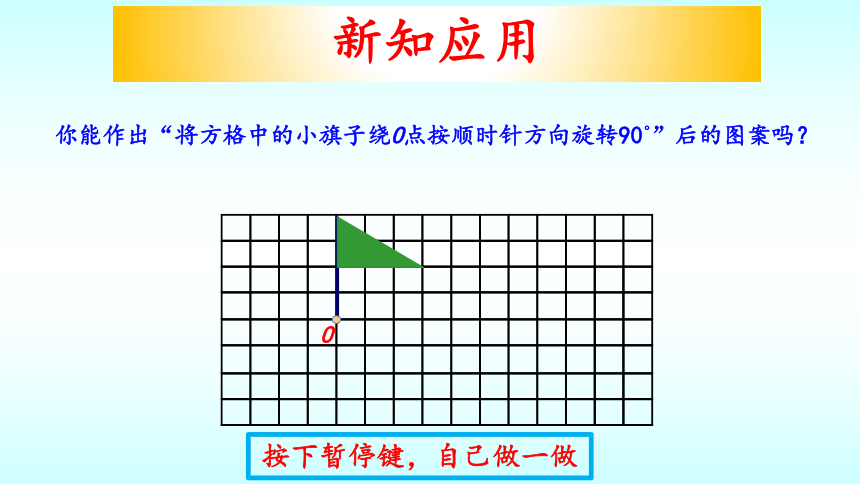
你能作出“将方格中的小旗子绕O点按顺时针方向旋转90?”后的图案吗?
O
新知应用
按下暂停键,自己做一做
A1
A
C
B
B1
C1
新知应用
【解析】
在原图上找了四个点即O点、A点、B点、C点,四个点是表示这面小旗子的关键点.
O
因为旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所组成的旋转角彼此相等,
所以根据已知:要把这面小旗绕O点按顺时针旋转90°.在方格中找到点A、B、C的对应点A1、B1、C1,然后连接,就得到了所求作的图形.
【例4】如图,△ABC绕C点旋转后,顶点A的对应点为点D.试确定旋转后的三角形位置,并叙述你的做法.
A
B
C
D
问题再探,提高升华
作图工具:尺、规、笔.
基本作图技能:
1.作一条线段等于已知线段;
2.作一个角等于已知角.
回顾已经学过的尺规作图
旋转作图
问题再探,提高升华
2.用旋转变换设计图案
甲
乙
A
B
知识运用,指导生活
怎样将甲图案变成乙图案?
甲
乙
A
B
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
按下暂停键,自己做一做
知识运用,指导生活
甲
乙
B
A
还可以用什么方法把甲图案变成乙图案?
知识运用,指导生活
可以先将甲图案沿AB方向将所得图案平移到B点位置,然后绕图上的B点旋转,使得图案被“扶直”, 即可得到乙图案
旋转
旋转中心?
旋转角?
旋转方向?
O
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
整个图形可以看作是右边的两个小“十”字A绕着图案的中心分别顺时针旋转90°、180°、270°得到D、C、B.
A
B
C
D
新知应用
按下暂停键,自己做一做
平移
平移的方向?
平移的距离?
仅靠平移无法得到
A
B
C
D
新知应用
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
平移、 旋转相结合
先平移
后旋转
O
整个图形可以看作是右边的两个小“十字” A先通过一次平移成图形左侧C的部分,然后A、C一起绕图形的中心顺时针旋转90°分别得到D 、B.
A
B
C
D
新知应用
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
轴对称
直线EF与GH相交于图形的中心O,且互相垂直,先把右边的两个“十字”A作关于GH的轴对称图形得到B,然后作这两部分关于EF的轴对称图形,这样就可以分别得到D、C.
E
F
G
H
O
对称轴?
新知应用
A
B
C
D
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
知识总结
①确定旋转的三要素:旋转中心、旋转方向、旋转角度.
从知识和思想上写一写本节课的收获.
图形之间的三种变换关系:
研究问题的方法:
轴对称、平移、旋转
转化思想:复杂问题简单化
旋转画图的一般思路:
按下暂停键,自己想一想
②将复杂图形的旋转转化成点的旋转.
1、同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到的 B.顺时针旋转120°得到的
C.逆时针旋转60°得到的 D.逆时针旋转120°得到的
当堂检测
2、将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
按下暂停键,自己做一做
1、同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
B
当堂检测
2、将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
过点O分别作各个顶点与点O连线的垂线,并在每条垂线上截取与相应线段长度相等的线段,得到各个顶点绕O点按顺时针方向旋转90°后的对应点,然后按原来的方式连接相应的顶点即可得到旋转后的图形(如图).
解:
当堂检测
1、在图中画出线段AB绕点O按顺时针方向旋转50°后的线段.
作业布置
2、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
按下暂停键,自己做一做
作业布置
3、在五边形ABCDE中,AB=AE、BC+DE=CD,∠ABC+∠AED=180°.
求证:DA平分∠CDE.
按下暂停键,自己做一做
1、在图中画出线段AB绕点O按顺时针方向旋转50°后的线段.
如图,过O在AB右侧作∠AOF=50°,在OF上截取OC=OA,延长FO,在FO的延长线上截取OD=OB,线段CD就是线段AB绕点O按顺时针方向旋转50°后的线段.
解:
作业参考答案
2、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解:(1)连接OA、OB、OC、OD、OE.
(2)分别以OB、OC、OD为边作∠BOF,∠COG,∠DOH,使∠BOF=∠COG=∠DOH=∠AOE.
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD.
(4)连接EF,FG,GH,HE.
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
作业参考答案
3、在五边形ABCDE中,AB=AE、BC+DE=CD,∠ABC+∠AED=180°.求证:DA平分∠CDE.
证明:连接AC,将△ABC绕点A逆时针旋转∠BAE的度数到△AEF的位置,
∵AB=AE,
∴AB与AE重合.
由旋转得:
∠AEF=∠ABC ,AF=AC,EF=BC.
∵∠ABC+∠AED=180°,且∠AEF=∠ABC,
∴∠AEF+∠AED=180°.
∴D,E,F三点在同一直线上,
∴ DF=DE+EF=DE+BC=DC,
作业参考答案
在△ADF与△ADC 中,
.
∴△ADF≌△ADC (SSS),
∴∠ADC=∠ADF,
即DA平分∠CDE.
初中数学八年级(下)
3.2 图形的旋转(第2课时)
知识回顾
1、什么叫旋转?
2、旋转的基本性质是什么?
按下暂停键,自己想一想
旋转前、后的图形全等:对应线段相等,对应角相等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转的基本性质:
知识回顾
旋转定义:
在平面内,将一个图形绕定点按一定方向转动一定角度 .这样的图形运动叫做旋转,这个定点称为旋转中心,转动的角称为 旋转角 .
动手操作,自主探究
旋转画图
作 图 工 具: 刻度尺、量角器、铅笔.
基本作图技能:1.画一条线段等于已知线段;
2.画一个角等于已知角.
点的旋转
【例1】试着找一找如图A点绕O点顺时针旋转30°后所在的位置A′.
A
O
A′
A
O
动手操作,自主探究
按下暂停键,自己做一做
点的旋转
【例1】试着找一找如图A点绕O点顺时针旋转30°后所在的位置A′.
A
O
A′
动手操作,自主探究
解:(1)以OA为一边按顺时针方向画∠AOX,使得∠AOX=30°.
(2)在射线OX上取点A′,使得OA′=OA.
点A′就是点A绕点O按顺时针方向旋转30°后的点.
X
【例2】在下图中,画出线段AB绕A点顺时针方向旋转60°后的线段.
线段的旋转
B
A
对于线段的旋转能不能看成是点的旋转呢?是不是只要找到点B绕着点A旋转后的对应点就可以了呢?
动手操作,自主探究
按下暂停键,自己做一做
【例2】在下图中,画出线段AB绕A点顺时针方向旋转60°后的线段.
线段的旋转
解:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
B
X
C
A
动手操作,自主探究
【例3】如图,△ABC绕点O按逆时针方向旋转后,
顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
图形的旋转
B
O
C
A
D
∠AOD
E
F
动手操作,自主探究
(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF就是所求作的三角形.
N
M
按下暂停键,自己做一做
总结:确定一个图形旋转后的位置的条件为:
①旋转中心、②旋转方向、③旋转角度.
确定一个图形旋转后的位置,需要哪些条件?
探究总结,形成认知
按下暂停键,自己想一想
你能作出“将方格中的小旗子绕O点按顺时针方向旋转90?”后的图案吗?
O
新知应用
按下暂停键,自己做一做
A1
A
C
B
B1
C1
新知应用
【解析】
在原图上找了四个点即O点、A点、B点、C点,四个点是表示这面小旗子的关键点.
O
因为旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所组成的旋转角彼此相等,
所以根据已知:要把这面小旗绕O点按顺时针旋转90°.在方格中找到点A、B、C的对应点A1、B1、C1,然后连接,就得到了所求作的图形.
【例4】如图,△ABC绕C点旋转后,顶点A的对应点为点D.试确定旋转后的三角形位置,并叙述你的做法.
A
B
C
D
问题再探,提高升华
作图工具:尺、规、笔.
基本作图技能:
1.作一条线段等于已知线段;
2.作一个角等于已知角.
回顾已经学过的尺规作图
旋转作图
问题再探,提高升华
2.用旋转变换设计图案
甲
乙
A
B
知识运用,指导生活
怎样将甲图案变成乙图案?
甲
乙
A
B
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
按下暂停键,自己做一做
知识运用,指导生活
甲
乙
B
A
还可以用什么方法把甲图案变成乙图案?
知识运用,指导生活
可以先将甲图案沿AB方向将所得图案平移到B点位置,然后绕图上的B点旋转,使得图案被“扶直”, 即可得到乙图案
旋转
旋转中心?
旋转角?
旋转方向?
O
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
整个图形可以看作是右边的两个小“十”字A绕着图案的中心分别顺时针旋转90°、180°、270°得到D、C、B.
A
B
C
D
新知应用
按下暂停键,自己做一做
平移
平移的方向?
平移的距离?
仅靠平移无法得到
A
B
C
D
新知应用
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
平移、 旋转相结合
先平移
后旋转
O
整个图形可以看作是右边的两个小“十字” A先通过一次平移成图形左侧C的部分,然后A、C一起绕图形的中心顺时针旋转90°分别得到D 、B.
A
B
C
D
新知应用
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
轴对称
直线EF与GH相交于图形的中心O,且互相垂直,先把右边的两个“十字”A作关于GH的轴对称图形得到B,然后作这两部分关于EF的轴对称图形,这样就可以分别得到D、C.
E
F
G
H
O
对称轴?
新知应用
A
B
C
D
下图由四部分组成,每部分都包括两个小“十字”,红色部分A能经过适当的图形变换得到其他三部分B、C、D吗?
知识总结
①确定旋转的三要素:旋转中心、旋转方向、旋转角度.
从知识和思想上写一写本节课的收获.
图形之间的三种变换关系:
研究问题的方法:
轴对称、平移、旋转
转化思想:复杂问题简单化
旋转画图的一般思路:
按下暂停键,自己想一想
②将复杂图形的旋转转化成点的旋转.
1、同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到的 B.顺时针旋转120°得到的
C.逆时针旋转60°得到的 D.逆时针旋转120°得到的
当堂检测
2、将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
按下暂停键,自己做一做
1、同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
B
当堂检测
2、将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
过点O分别作各个顶点与点O连线的垂线,并在每条垂线上截取与相应线段长度相等的线段,得到各个顶点绕O点按顺时针方向旋转90°后的对应点,然后按原来的方式连接相应的顶点即可得到旋转后的图形(如图).
解:
当堂检测
1、在图中画出线段AB绕点O按顺时针方向旋转50°后的线段.
作业布置
2、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
按下暂停键,自己做一做
作业布置
3、在五边形ABCDE中,AB=AE、BC+DE=CD,∠ABC+∠AED=180°.
求证:DA平分∠CDE.
按下暂停键,自己做一做
1、在图中画出线段AB绕点O按顺时针方向旋转50°后的线段.
如图,过O在AB右侧作∠AOF=50°,在OF上截取OC=OA,延长FO,在FO的延长线上截取OD=OB,线段CD就是线段AB绕点O按顺时针方向旋转50°后的线段.
解:
作业参考答案
2、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解:(1)连接OA、OB、OC、OD、OE.
(2)分别以OB、OC、OD为边作∠BOF,∠COG,∠DOH,使∠BOF=∠COG=∠DOH=∠AOE.
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD.
(4)连接EF,FG,GH,HE.
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
作业参考答案
3、在五边形ABCDE中,AB=AE、BC+DE=CD,∠ABC+∠AED=180°.求证:DA平分∠CDE.
证明:连接AC,将△ABC绕点A逆时针旋转∠BAE的度数到△AEF的位置,
∵AB=AE,
∴AB与AE重合.
由旋转得:
∠AEF=∠ABC ,AF=AC,EF=BC.
∵∠ABC+∠AED=180°,且∠AEF=∠ABC,
∴∠AEF+∠AED=180°.
∴D,E,F三点在同一直线上,
∴ DF=DE+EF=DE+BC=DC,
作业参考答案
在△ADF与△ADC 中,
.
∴△ADF≌△ADC (SSS),
∴∠ADC=∠ADF,
即DA平分∠CDE.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
