7.7 动能和动能定理 经典课件(共44张PPT)
文档属性
| 名称 | 7.7 动能和动能定理 经典课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-08 13:28:15 | ||
图片预览










文档简介
(共44张PPT)
物体由于运动而具有的能量叫做动能。
在本章“1.追寻守恒量”中,已经知道
龙卷风
海啸
风力发电
与物体的质量和速度有关
思考:物体的动能与哪些因素有 关?是什么样的关系?
结论:物体的质量越大,速度越大,它的动能就 越大。
那么,动能与物体的质量和速度之间有什么定量的关系呢?
一、探究动能的表达式
重力做功WG
重力势能mgh
弹力做功WF
外力做功 w
弹性势能kx2/2
动能表达式?
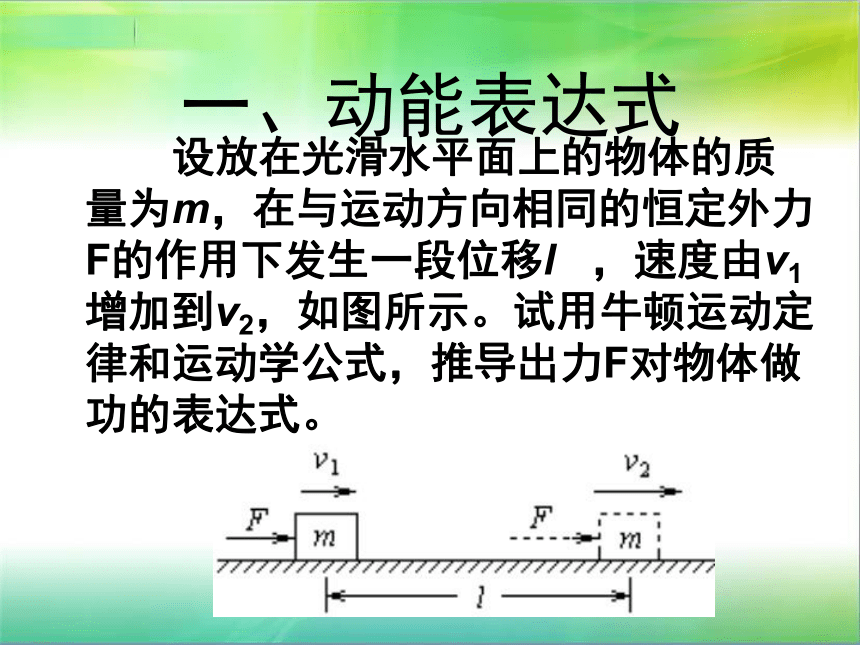
一、动能表达式
设放在光滑水平面上的物体的质量为m,在与运动方向相同的恒定外力F的作用下发生一段位移l ,速度由v1增加到v2,如图所示。试用牛顿运动定律和运动学公式,推导出力F对物体做功的表达式。
根据牛顿第二定律
结果与思考
初态和末态的表达式均为“mv2/2”,这个“mv2/2”代表什么?
末态
初态
功的表达式为:
从上面式子可以看出, 很可能是一
个具有特定意义的物理量。因为这个量
在过程终了时和过程开始时的差,刚好
等于力对物体做的功,所以 应该
是我们寻找的动能的表达式。
m为物体的质量
v为物体的瞬时速度
单位:焦耳(J)
二.动能
我们对动能的表达式Ek=mv2/2的理解
1、动能是标量,且只有正值,动能只与物体的速度大小有关,与速度方向无关。
2、动能是状态量.V是瞬时速度。在某一时刻,物体具有一定的速度,也就具有一定的动能。
3、动能具有相对性,对不同的参考系,物体速度有不同的瞬时值,也就具有不同的动能,一般都以地面为参考系研究物体的运动。
我们知道,运动是相对的。当鸟儿与飞机相对而行时,虽然鸟儿的速度不是很大,但是飞机的飞行速度很大,这样对于飞机来说,鸟儿的速度就很大。速度越大,撞击的力量就越大。
比如一只0.45千克的鸟,撞在速度为每小时80千米的飞机上时,就会产生1500牛顿的力,要是撞在速度为每小时960千米的飞机上,那就要产生21.6万牛顿的力。如果是一只1.8千克的鸟撞在速度为每小时 700千米的飞机上,产生的冲击力比炮弹的冲击力还要大。所以浑身是肉的鸟儿也能变成击落飞机的“炮弹”。
1962年11月,赫赫有名的“子爵号”飞机正在美国马里兰州伊利奥特市上空平稳地飞行,突然一声巨响,飞机从高空栽了下来。事后发现酿成这场空中悲剧的罪魁就是一只在空中慢慢翱翔的天鹅。
鸟击落飞机
对动能相对性的理解
鸟本身速度不快,质量也不大,但相对于飞机来说,由于飞机速度很快,所以它们相互靠近的速度很快,因此,鸟相对飞机的速度很快,具有很大的相对动能,当两者相撞时,会造成严重的空难事故。
试比较下列每种情况下,甲、乙两物体的动能:(除题意中提到的物理量外,其他物理情况相同)
总结:动能是标量,与速度方向无关;动能与
速度的平方成正比,因此速度对动能的
影响更大。
①物体甲的速度是乙的两倍;
②物体甲向北运动,乙向南运动;
③物体甲做直线运动,乙做曲线运动;
④物体甲的质量是乙的一半。
关于动能的理解,下列说法正确的是:
A、一定质量的物体,速度变化时,动能一定变化。
B、一定质量的物体,速度不变时,动能一定不变。
C、一定质量的物体,动能变化时,速度一定变化。
D、一定质量的物体,动能不变时,速度一定不变。
随堂练习
W=Ek2-Ek1=△Ek
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
三.动能定理
思考与讨论(一)
如果物体受到几个力作用,动能定理中的W表示的物理意义是什么?
合力所做的总功。
动能定理表述为:
合 力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
举例说明
上一节课做实验探究物体速度与力做功之间的关系时,曾经采用的一种方法是平衡摩擦力,实际上这时小车受到的橡皮筋的拉力就等于物体所受的合力.
一架飞机在牵引力和阻力的共同作用下,在跑道上加速运动.速度越来越大,动能越来越大.这个过程中是牵引力和阻力都做功,牵引力做正功,阻力做负功,牵引力和阻力的合力做了多少功,飞机的动能就变化了多少.
思考与讨论(二)
动能定理是否可以应用于变力做功或物体做曲线运动的情况,该怎样理解?
把过程分解为很多小段,认为物体在每小段运动中受到的力是恒力,运动的轨迹是直线,这样也能得到动能定理.
对动能定理的理解
1、动能是标量,只有正值,但△Ek有正负之分。
当外力做正功时,W>0,故Ek2>Ek1,即动能增加
当外力做负功时,W<0,故Ek2动能定理表明了数值上是相等的,并不意味着功就是动能增量,也不是功转变成动能,而是功引起物体动能的变化。
2.动能定理是标量式,式中的速度是相对于同一参考系,一般指相对于地面。
3.对单一物体的单一过程,w指合外力做的功,若对某一过程的不同阶段,物体受力情况发生变化,则w应是所有外力所做的总功,各力做功的代数和。
4、对状态与过程关系的理解
功是伴随一个物理过程而产生的,是过程量;而动能是状态量。 动能定理表示了过程量等于状态量的改变量的关系。
5、适用范围:
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
应用动能定理解题一般步骤(尤其是变力功、曲线运动):
1.明确对象和过程:(通常是单个物体)
2.作二分析:
⑴受力分析,确定各力做功及其正负
⑵确定初、末速度,明确初末状态的动能
3.由动能定理列方程:
W合=mv22/2-mv12/2
动能定理的应用
1、常规题(匀变速直线运动)
2、求变力做功问题
4、多过程问题
3、求解曲线运动问题
5、其它问题
例:一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。
v0=0m/s
v=60m/s
s=5.3×102m
例1、一架喷气式飞机,质量 ,起飞过程中从静止开始滑跑的路程为 时,达到起飞速度 。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
应用1:恒力+直线运动
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
例4、在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为( )
C
应用2:恒力+曲线运动
不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关,在涉及有关的力学问题,优先应用动能定理。
应用3:变力做功
多过程问题 (直线运动)
斜面倾角为α,长为l, AB段光滑,BC段粗糙,AB =l/3, 质量为m的木块从斜面顶端无初速下滑,到达C端时速度刚好为零。求物体与BC段间的动摩擦因数μ。
分析:小球的下落过程根据受力情况可分为两段:
应用4:多过程
1.一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
因此可以分两段求解,也可以按全过程求解
接触地面前做自由落体运动,只受重力G作用;
接触地面后做减速运动,受重力G和阻力f作用。
接触地面前
(2)全过程:
解:以球为研究对象,在下落的过程中受力如图,根据动能定理有
解 得:
(1)分段求解
设小球在接触地面时的速度为v,则
接触地面后
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求物块从·B点到c点克服阻力所做的的功?
如图所示,倾角为37度的斜面底端B平滑连接着半径为r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距离地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数为0.25。求
1.物块滑到斜面底端B时的速度大小;
2.物块运动到圆轨道的最高点A时,对圆轨道的压力大小。
课堂小结
一、动能
1、定义:物体由于运动而具有的能量叫做动能
2、表达式:
3、单位:焦耳(J)
二、动能定理
1、内容:合力所做的功等于物体动能的变化
2、表达式:
返回
变力功
高考是怎样考的
一物块由静止开始从粗糙斜面上的某点加速下滑到另一点,在此过程中重力对物块做的功等于(05辽宁):
A.物块动能的增加量
B.物块重力势能的减少量与物块克服摩擦力做的功之和
C.物块重力势能的减少量和物块动能的增加量以及物块克服摩擦力做的功之和
D.物块动能的增加量与物块克服摩擦力做的功之和
物体由于运动而具有的能量叫做动能。
在本章“1.追寻守恒量”中,已经知道
龙卷风
海啸
风力发电
与物体的质量和速度有关
思考:物体的动能与哪些因素有 关?是什么样的关系?
结论:物体的质量越大,速度越大,它的动能就 越大。
那么,动能与物体的质量和速度之间有什么定量的关系呢?
一、探究动能的表达式
重力做功WG
重力势能mgh
弹力做功WF
外力做功 w
弹性势能kx2/2
动能表达式?
一、动能表达式
设放在光滑水平面上的物体的质量为m,在与运动方向相同的恒定外力F的作用下发生一段位移l ,速度由v1增加到v2,如图所示。试用牛顿运动定律和运动学公式,推导出力F对物体做功的表达式。
根据牛顿第二定律
结果与思考
初态和末态的表达式均为“mv2/2”,这个“mv2/2”代表什么?
末态
初态
功的表达式为:
从上面式子可以看出, 很可能是一
个具有特定意义的物理量。因为这个量
在过程终了时和过程开始时的差,刚好
等于力对物体做的功,所以 应该
是我们寻找的动能的表达式。
m为物体的质量
v为物体的瞬时速度
单位:焦耳(J)
二.动能
我们对动能的表达式Ek=mv2/2的理解
1、动能是标量,且只有正值,动能只与物体的速度大小有关,与速度方向无关。
2、动能是状态量.V是瞬时速度。在某一时刻,物体具有一定的速度,也就具有一定的动能。
3、动能具有相对性,对不同的参考系,物体速度有不同的瞬时值,也就具有不同的动能,一般都以地面为参考系研究物体的运动。
我们知道,运动是相对的。当鸟儿与飞机相对而行时,虽然鸟儿的速度不是很大,但是飞机的飞行速度很大,这样对于飞机来说,鸟儿的速度就很大。速度越大,撞击的力量就越大。
比如一只0.45千克的鸟,撞在速度为每小时80千米的飞机上时,就会产生1500牛顿的力,要是撞在速度为每小时960千米的飞机上,那就要产生21.6万牛顿的力。如果是一只1.8千克的鸟撞在速度为每小时 700千米的飞机上,产生的冲击力比炮弹的冲击力还要大。所以浑身是肉的鸟儿也能变成击落飞机的“炮弹”。
1962年11月,赫赫有名的“子爵号”飞机正在美国马里兰州伊利奥特市上空平稳地飞行,突然一声巨响,飞机从高空栽了下来。事后发现酿成这场空中悲剧的罪魁就是一只在空中慢慢翱翔的天鹅。
鸟击落飞机
对动能相对性的理解
鸟本身速度不快,质量也不大,但相对于飞机来说,由于飞机速度很快,所以它们相互靠近的速度很快,因此,鸟相对飞机的速度很快,具有很大的相对动能,当两者相撞时,会造成严重的空难事故。
试比较下列每种情况下,甲、乙两物体的动能:(除题意中提到的物理量外,其他物理情况相同)
总结:动能是标量,与速度方向无关;动能与
速度的平方成正比,因此速度对动能的
影响更大。
①物体甲的速度是乙的两倍;
②物体甲向北运动,乙向南运动;
③物体甲做直线运动,乙做曲线运动;
④物体甲的质量是乙的一半。
关于动能的理解,下列说法正确的是:
A、一定质量的物体,速度变化时,动能一定变化。
B、一定质量的物体,速度不变时,动能一定不变。
C、一定质量的物体,动能变化时,速度一定变化。
D、一定质量的物体,动能不变时,速度一定不变。
随堂练习
W=Ek2-Ek1=△Ek
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
三.动能定理
思考与讨论(一)
如果物体受到几个力作用,动能定理中的W表示的物理意义是什么?
合力所做的总功。
动能定理表述为:
合 力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
举例说明
上一节课做实验探究物体速度与力做功之间的关系时,曾经采用的一种方法是平衡摩擦力,实际上这时小车受到的橡皮筋的拉力就等于物体所受的合力.
一架飞机在牵引力和阻力的共同作用下,在跑道上加速运动.速度越来越大,动能越来越大.这个过程中是牵引力和阻力都做功,牵引力做正功,阻力做负功,牵引力和阻力的合力做了多少功,飞机的动能就变化了多少.
思考与讨论(二)
动能定理是否可以应用于变力做功或物体做曲线运动的情况,该怎样理解?
把过程分解为很多小段,认为物体在每小段运动中受到的力是恒力,运动的轨迹是直线,这样也能得到动能定理.
对动能定理的理解
1、动能是标量,只有正值,但△Ek有正负之分。
当外力做正功时,W>0,故Ek2>Ek1,即动能增加
当外力做负功时,W<0,故Ek2
2.动能定理是标量式,式中的速度是相对于同一参考系,一般指相对于地面。
3.对单一物体的单一过程,w指合外力做的功,若对某一过程的不同阶段,物体受力情况发生变化,则w应是所有外力所做的总功,各力做功的代数和。
4、对状态与过程关系的理解
功是伴随一个物理过程而产生的,是过程量;而动能是状态量。 动能定理表示了过程量等于状态量的改变量的关系。
5、适用范围:
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
应用动能定理解题一般步骤(尤其是变力功、曲线运动):
1.明确对象和过程:(通常是单个物体)
2.作二分析:
⑴受力分析,确定各力做功及其正负
⑵确定初、末速度,明确初末状态的动能
3.由动能定理列方程:
W合=mv22/2-mv12/2
动能定理的应用
1、常规题(匀变速直线运动)
2、求变力做功问题
4、多过程问题
3、求解曲线运动问题
5、其它问题
例:一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。
v0=0m/s
v=60m/s
s=5.3×102m
例1、一架喷气式飞机,质量 ,起飞过程中从静止开始滑跑的路程为 时,达到起飞速度 。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
应用1:恒力+直线运动
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
例4、在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为( )
C
应用2:恒力+曲线运动
不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关,在涉及有关的力学问题,优先应用动能定理。
应用3:变力做功
多过程问题 (直线运动)
斜面倾角为α,长为l, AB段光滑,BC段粗糙,AB =l/3, 质量为m的木块从斜面顶端无初速下滑,到达C端时速度刚好为零。求物体与BC段间的动摩擦因数μ。
分析:小球的下落过程根据受力情况可分为两段:
应用4:多过程
1.一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
因此可以分两段求解,也可以按全过程求解
接触地面前做自由落体运动,只受重力G作用;
接触地面后做减速运动,受重力G和阻力f作用。
接触地面前
(2)全过程:
解:以球为研究对象,在下落的过程中受力如图,根据动能定理有
解 得:
(1)分段求解
设小球在接触地面时的速度为v,则
接触地面后
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求物块从·B点到c点克服阻力所做的的功?
如图所示,倾角为37度的斜面底端B平滑连接着半径为r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距离地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数为0.25。求
1.物块滑到斜面底端B时的速度大小;
2.物块运动到圆轨道的最高点A时,对圆轨道的压力大小。
课堂小结
一、动能
1、定义:物体由于运动而具有的能量叫做动能
2、表达式:
3、单位:焦耳(J)
二、动能定理
1、内容:合力所做的功等于物体动能的变化
2、表达式:
返回
变力功
高考是怎样考的
一物块由静止开始从粗糙斜面上的某点加速下滑到另一点,在此过程中重力对物块做的功等于(05辽宁):
A.物块动能的增加量
B.物块重力势能的减少量与物块克服摩擦力做的功之和
C.物块重力势能的减少量和物块动能的增加量以及物块克服摩擦力做的功之和
D.物块动能的增加量与物块克服摩擦力做的功之和
