高中数学人教新课标A版选修3-4第一讲平面图形的对称群1.1 平面刚体运动(共39张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-4第一讲平面图形的对称群1.1 平面刚体运动(共39张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 738.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 10:55:00 | ||
图片预览










文档简介
(共39张PPT)
旧知回顾
对称图形有什么特点?
在一张纸(平面)上画一个等腰△ABC,在它的底边的垂直平分线AD处放一面“双面镜”,并使镜面与纸面垂直,在镜面的反射下,△ABC被映射成了什么图形?这个图形与△ABC有什么关系?
一个正方形ABCD绕它的中心O逆时针旋转180°后,变成了什么图形?得到的图形与原来的图形有什么关系?
【知识与能力】
了解平面刚体运动的定义,区分它
与对称定义的区别和联系.
掌握平面刚体运动的特点、性质.
学会寻找不动点.
【过程与方法】
通过丰富的实例,让学生合作探讨,老师分析点评,与前面所学的知识进行对比学习.经过对比掌握平面刚体运动的定义和性质.
结合课本所给的例子,进行简绍.
【情感态度与价值观】
通过前后知识的对比,得出平面刚体运动的定义及其性质,学习各种变换的特点,使同学们体会到,探索在某种变换下的不变量或不变关系,是数学研究的重要问题.
平面刚体运动的定义、性质
不动点
我们现在用整个平面来代替思考一当中的等腰三角形,来考察整个平面关于“双镜面”的反射.
我们知道,一个平面可以看成是点的集合,就像我们把直线看成点的集合一样.
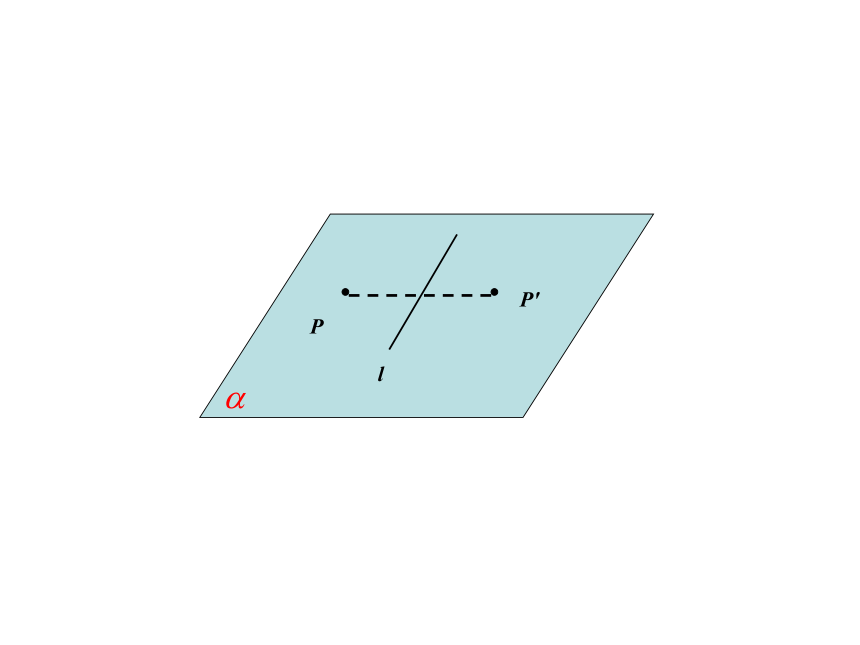
设α是一个由平面内的所有点组成的集合,l是这个平面内的一条直线,定义点集α(平面) 到其自身的一个映射
r: P →P′ ,
r 把平面α内的任意一点P 映到点P关于直线 l 的对称点P′,我们把这个映射称为平面α关于直线 l 的反射.数学上,把这样定义的反射称为平面α的一个反射变换.
可以知道,在反射变换 r 的作用下,平面α 内的点,平面α内的图形被映到了与它全等的图形.
这时,如果一个平面图形在映射 r 的作用下仍与原来的图形重合,我们就称这个图形是一个轴对称图形.
按照这个定义,引言中的等腰梯形、正五边形都是轴对称图形?这个定义与引言中的定义1是等价的吗?
现在,我们考虑整个平面内一个固定点逆时针转180°的旋转,准确地说,设α是一个平面内所有点构成的集合,O是平面α内的一个固定点,定义点集(平面) α到其自身的一个映射
ρ:P→P′
把平面 内的任意一点P绕点O旋转180°后映到点P ′,这个映射称为以点O为中心转180°的旋转.
在看一下正方形的旋转,取正方形ABCD的中心O为固定点,设ρ是以点O为中心转180°的旋转.那么在ρ的作用下,正方形上任意一点P被映到了正方形上另一点P′,正方形的顶点A,B,C,D依次被映到点C,D,A,B,正方形ABCD被映到正方形CDAB,显然这两个正方形重合.
若没有特别说明,旋转的方向都是指逆时针方向.
一般地,如果一个平面图形在影射ρ(以点O为中心转180°的旋转)的作用下仍与原来的图形重合,我们就称这个平面图形是一个中心对称图形.
按照这个定义,引言中的平行四边形、正六边形、圆都是中心对称图形吗?这个定义与引言中的定义2是等价的吗?
我们可以对以O为中心转180°的旋转进行推广,把旋转180°改为任意角度,这样我们就可以定义一个映射,来表示平面以一个固定点P为中心转任意给定角度的旋转.这样定义的映射在数学上称为旋转变换.
特别地,旋转角度为0°的旋转变换是把平面上的所有点映射到它自身,这个映射使整个平面上的每个点都保持不动,所以称为恒等变换.
设P,Q是平面内的任意两点,在旋转(或反射)变换的作用下,它们的对应点分别是P′,Q′.P′到Q′的距离与P到Q的距离有什么关系?
结论
可以发现,反射变换和旋转变换有一个共同的特点,即所谓的“保距性”.也就是说,对于平面内的任意两点P和Q,在反射(或旋转)变换的作用下的对应点是P′和Q′,那么P′到Q′的距离等于P到Q的距离.
设α是一个平面,映射
m:平面α →平面α
是一个一一映射,若m保持平面α内任意两点间的距离不变,则称m是一个平面刚体运动.
下面我们对上述定义作一个简单的解释。任意一个平面刚体运动m: 平面α →平面 α ,都满足下面四条:
(1) 对于平面α内的任意一点P,在平面α 内存在唯一的一点P′与之对应,记作P′=m(P),P′叫做P在m作用下的象;
(2)任取平面α内的一点P′,存在平面 α 内的点P,使得P′是P在变换m作用下的象;
(3)任取平面α内的两点P1,P2,如果P1≠P2,那么它们的象也是不同的,即m(P1)≠m(P2);
(4)任取平面α内的两点P,Q,使它们在m下的象是P′,Q′即 P′=m(P),Q′=m(Q),那么|P′Q′|=|PQ|,即点P′,Q′之间的距离与点P,Q之间的距离相等.
你能举出一些平面刚体运动的例子吗?
实际上,我们在过去的学习中碰到过许多平面刚体运动.例如,我们熟悉的平移就是一平面刚体运动.
设α是一个平面,点O是α内的一个定点,v是一个以O为起点的定向量,平移是指平面内一个点到点的映射
t:P→P′,
t 把平面内的任意一点P映射到点P′,且满足
这个映射在数学上称为平移变换.在平移变换t的作用下,平面内的所有点沿着定向量v的方向,移动了距离|v|.
平面刚体运动m:平面 →平面 有哪些性质呢?保持距离不变是m的一个很强的性质.可以证明,只要知道不共线的3个点A,B,C在m下的象A,B,C,m就完全确定下来了.
平面刚体运动
m:平面α →平面α
将平面α内的直线映成直线,射线映成射线,线段映成等长的线段.
证明:令l是平面α内的任意一条直线,设m把l上所有的点映到点集l′.
在l上任取两点A,B,设m把它们分别映到A′,B′.下面我们来证明l′是过点A′,B′的直线.
在AB上任取一点C,设m把点C映射到点C′.
(1)如下图,当点C在AB之间时,由平面刚体运动的定义得
|A′C′|+|C′B′|=|AC|+|CB|
=|AB|=|A′B′|
所以点C′在线段A′B′上.
↓m
(2)如下图,当点C在AB的延长线上时,我们有 |A′B′|+|B′C′|=|AB|+|BC|
=|AC|=|A′C′|
所以点B′在线段A′C′上,即点C′在线段A′B′的延长线上.
↓m
同理可证,当点C在BA的延长线上时,点C′在线段B′A′的延长线上.
由点A,B,C的任意性可知,l′是一条直线.
如何证明平面刚体运动m:平面α →平面α将平面α上的射线映成射线,线段映成等长的线段?
下面,我们说明三角形在平面刚体运动的作用下,形状和大小都保持不变.
如下图,设△ABC是平面α内的任意一个三角形,由已证命题可知,平面刚体运动
m:平面α →平面α
把线段AB,BC,AC依次映成线段A′B′,B′C′,A′C′.
而且
AB=A′B′,BC=B′C′,AC=A′C′.
由于
AB+BC>AC,
故
A′B′+B′C′>A′C′,
所以A′B′,B′C′,C′A′构成了一个以A′,B′,C′为顶点的三角形,而且△ABC与△A′B′C′是全等的.
最后,我们讨论一类特殊的平面刚体运动.设
m:平面α →平面α
是一个平面刚体运动,若在平面α内至少存在一个点O,点O在m的作用下保持不动,即m(O)=O,我们称m为有不动点的平面刚体运动.
1.平面刚体运动的定义
设α是一个平面,映射
m:平面α →平面α
是一个一一映射,若m保持平面α内任意两点间的距离不变,则称m是一个平面刚体运动.
2.平面刚体运动的性质
平面刚体运动
m:平面α →平面α
将平面α内的直线映成直线,射线映成射线,线段映成等长的线段.
旧知回顾
对称图形有什么特点?
在一张纸(平面)上画一个等腰△ABC,在它的底边的垂直平分线AD处放一面“双面镜”,并使镜面与纸面垂直,在镜面的反射下,△ABC被映射成了什么图形?这个图形与△ABC有什么关系?
一个正方形ABCD绕它的中心O逆时针旋转180°后,变成了什么图形?得到的图形与原来的图形有什么关系?
【知识与能力】
了解平面刚体运动的定义,区分它
与对称定义的区别和联系.
掌握平面刚体运动的特点、性质.
学会寻找不动点.
【过程与方法】
通过丰富的实例,让学生合作探讨,老师分析点评,与前面所学的知识进行对比学习.经过对比掌握平面刚体运动的定义和性质.
结合课本所给的例子,进行简绍.
【情感态度与价值观】
通过前后知识的对比,得出平面刚体运动的定义及其性质,学习各种变换的特点,使同学们体会到,探索在某种变换下的不变量或不变关系,是数学研究的重要问题.
平面刚体运动的定义、性质
不动点
我们现在用整个平面来代替思考一当中的等腰三角形,来考察整个平面关于“双镜面”的反射.
我们知道,一个平面可以看成是点的集合,就像我们把直线看成点的集合一样.
设α是一个由平面内的所有点组成的集合,l是这个平面内的一条直线,定义点集α(平面) 到其自身的一个映射
r: P →P′ ,
r 把平面α内的任意一点P 映到点P关于直线 l 的对称点P′,我们把这个映射称为平面α关于直线 l 的反射.数学上,把这样定义的反射称为平面α的一个反射变换.
可以知道,在反射变换 r 的作用下,平面α 内的点,平面α内的图形被映到了与它全等的图形.
这时,如果一个平面图形在映射 r 的作用下仍与原来的图形重合,我们就称这个图形是一个轴对称图形.
按照这个定义,引言中的等腰梯形、正五边形都是轴对称图形?这个定义与引言中的定义1是等价的吗?
现在,我们考虑整个平面内一个固定点逆时针转180°的旋转,准确地说,设α是一个平面内所有点构成的集合,O是平面α内的一个固定点,定义点集(平面) α到其自身的一个映射
ρ:P→P′
把平面 内的任意一点P绕点O旋转180°后映到点P ′,这个映射称为以点O为中心转180°的旋转.
在看一下正方形的旋转,取正方形ABCD的中心O为固定点,设ρ是以点O为中心转180°的旋转.那么在ρ的作用下,正方形上任意一点P被映到了正方形上另一点P′,正方形的顶点A,B,C,D依次被映到点C,D,A,B,正方形ABCD被映到正方形CDAB,显然这两个正方形重合.
若没有特别说明,旋转的方向都是指逆时针方向.
一般地,如果一个平面图形在影射ρ(以点O为中心转180°的旋转)的作用下仍与原来的图形重合,我们就称这个平面图形是一个中心对称图形.
按照这个定义,引言中的平行四边形、正六边形、圆都是中心对称图形吗?这个定义与引言中的定义2是等价的吗?
我们可以对以O为中心转180°的旋转进行推广,把旋转180°改为任意角度,这样我们就可以定义一个映射,来表示平面以一个固定点P为中心转任意给定角度的旋转.这样定义的映射在数学上称为旋转变换.
特别地,旋转角度为0°的旋转变换是把平面上的所有点映射到它自身,这个映射使整个平面上的每个点都保持不动,所以称为恒等变换.
设P,Q是平面内的任意两点,在旋转(或反射)变换的作用下,它们的对应点分别是P′,Q′.P′到Q′的距离与P到Q的距离有什么关系?
结论
可以发现,反射变换和旋转变换有一个共同的特点,即所谓的“保距性”.也就是说,对于平面内的任意两点P和Q,在反射(或旋转)变换的作用下的对应点是P′和Q′,那么P′到Q′的距离等于P到Q的距离.
设α是一个平面,映射
m:平面α →平面α
是一个一一映射,若m保持平面α内任意两点间的距离不变,则称m是一个平面刚体运动.
下面我们对上述定义作一个简单的解释。任意一个平面刚体运动m: 平面α →平面 α ,都满足下面四条:
(1) 对于平面α内的任意一点P,在平面α 内存在唯一的一点P′与之对应,记作P′=m(P),P′叫做P在m作用下的象;
(2)任取平面α内的一点P′,存在平面 α 内的点P,使得P′是P在变换m作用下的象;
(3)任取平面α内的两点P1,P2,如果P1≠P2,那么它们的象也是不同的,即m(P1)≠m(P2);
(4)任取平面α内的两点P,Q,使它们在m下的象是P′,Q′即 P′=m(P),Q′=m(Q),那么|P′Q′|=|PQ|,即点P′,Q′之间的距离与点P,Q之间的距离相等.
你能举出一些平面刚体运动的例子吗?
实际上,我们在过去的学习中碰到过许多平面刚体运动.例如,我们熟悉的平移就是一平面刚体运动.
设α是一个平面,点O是α内的一个定点,v是一个以O为起点的定向量,平移是指平面内一个点到点的映射
t:P→P′,
t 把平面内的任意一点P映射到点P′,且满足
这个映射在数学上称为平移变换.在平移变换t的作用下,平面内的所有点沿着定向量v的方向,移动了距离|v|.
平面刚体运动m:平面 →平面 有哪些性质呢?保持距离不变是m的一个很强的性质.可以证明,只要知道不共线的3个点A,B,C在m下的象A,B,C,m就完全确定下来了.
平面刚体运动
m:平面α →平面α
将平面α内的直线映成直线,射线映成射线,线段映成等长的线段.
证明:令l是平面α内的任意一条直线,设m把l上所有的点映到点集l′.
在l上任取两点A,B,设m把它们分别映到A′,B′.下面我们来证明l′是过点A′,B′的直线.
在AB上任取一点C,设m把点C映射到点C′.
(1)如下图,当点C在AB之间时,由平面刚体运动的定义得
|A′C′|+|C′B′|=|AC|+|CB|
=|AB|=|A′B′|
所以点C′在线段A′B′上.
↓m
(2)如下图,当点C在AB的延长线上时,我们有 |A′B′|+|B′C′|=|AB|+|BC|
=|AC|=|A′C′|
所以点B′在线段A′C′上,即点C′在线段A′B′的延长线上.
↓m
同理可证,当点C在BA的延长线上时,点C′在线段B′A′的延长线上.
由点A,B,C的任意性可知,l′是一条直线.
如何证明平面刚体运动m:平面α →平面α将平面α上的射线映成射线,线段映成等长的线段?
下面,我们说明三角形在平面刚体运动的作用下,形状和大小都保持不变.
如下图,设△ABC是平面α内的任意一个三角形,由已证命题可知,平面刚体运动
m:平面α →平面α
把线段AB,BC,AC依次映成线段A′B′,B′C′,A′C′.
而且
AB=A′B′,BC=B′C′,AC=A′C′.
由于
AB+BC>AC,
故
A′B′+B′C′>A′C′,
所以A′B′,B′C′,C′A′构成了一个以A′,B′,C′为顶点的三角形,而且△ABC与△A′B′C′是全等的.
最后,我们讨论一类特殊的平面刚体运动.设
m:平面α →平面α
是一个平面刚体运动,若在平面α内至少存在一个点O,点O在m的作用下保持不动,即m(O)=O,我们称m为有不动点的平面刚体运动.
1.平面刚体运动的定义
设α是一个平面,映射
m:平面α →平面α
是一个一一映射,若m保持平面α内任意两点间的距离不变,则称m是一个平面刚体运动.
2.平面刚体运动的性质
平面刚体运动
m:平面α →平面α
将平面α内的直线映成直线,射线映成射线,线段映成等长的线段.
