高中数学人教新课标A版选修3-4第一讲平面图形的对称群1.2 对称变换(共50张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-4第一讲平面图形的对称群1.2 对称变换(共50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:01:08 | ||
图片预览






文档简介
(共50张PPT)
回顾旧知
从上一节的讨论发现,我们可以利用平面刚体运动来定义平面图形的对称性.
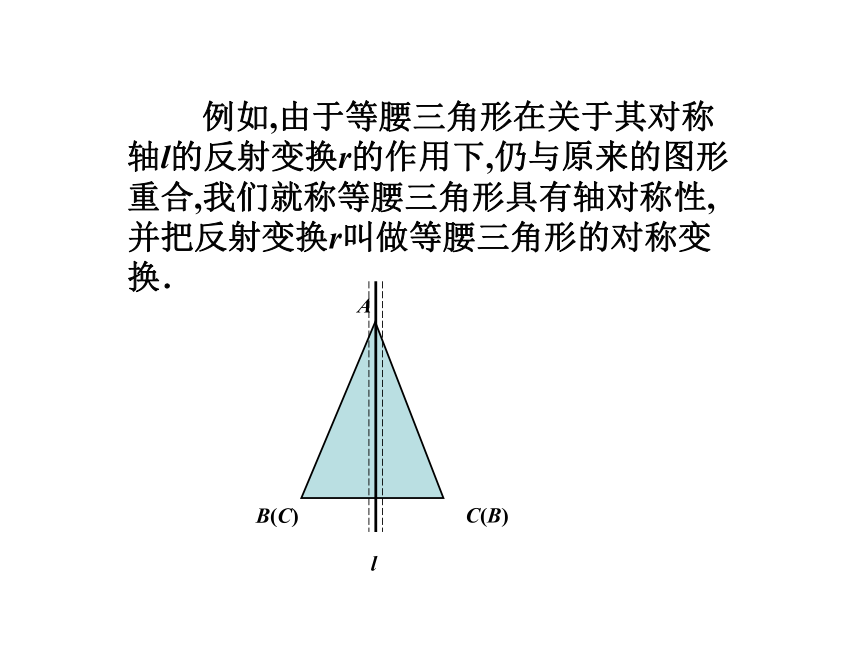
例如,由于等腰三角形在关于其对称轴l的反射变换r的作用下,仍与原来的图形重合,我们就称等腰三角形具有轴对称性,并把反射变换r叫做等腰三角形的对称变换.
A
B(C)
C(B)
l
动动脑
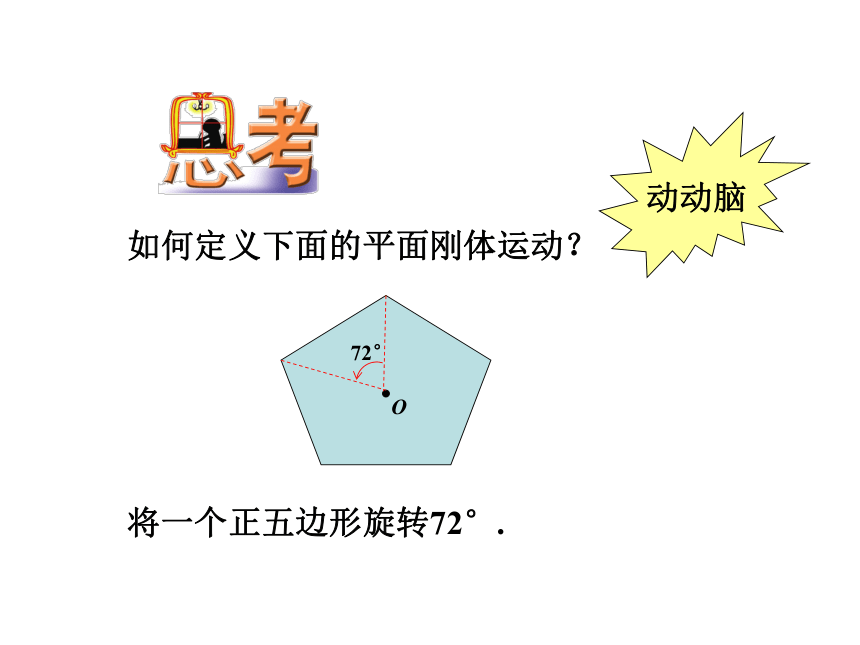
如何定义下面的平面刚体运动?
将一个正五边形旋转72°.
72°
O
准确掌握对称变换的概念.
掌握对称变换的合成和其性质.
了解对称变换的逆变换.
【知识与能力】
通过观察、操作,了解平面图形“对称”的概念推广过程.
进一步了解对称变换的特点.
通过实例来简绍对称变换的合成、性质和逆变换.
【过程与方法】
让学生从实例中体会数学概念的导出.
对大量的实例进行观察,得出规律.
培养合作交流意识.
【情感态度与价值观】
对称变换的定义、性质
对称变换的合成、逆变换
若一个平面图形K在平面刚体运动m的作用下仍与原来的图形重合,就称K具有对称性,m叫做K的对称变换.
按照上述定义,“一个平面图形是对称图形”等价于说“一个平面图形有对称变换”.
显然,任意图形都在恒等变换下变到自身,这时我们也认为这个图形具有对称性.
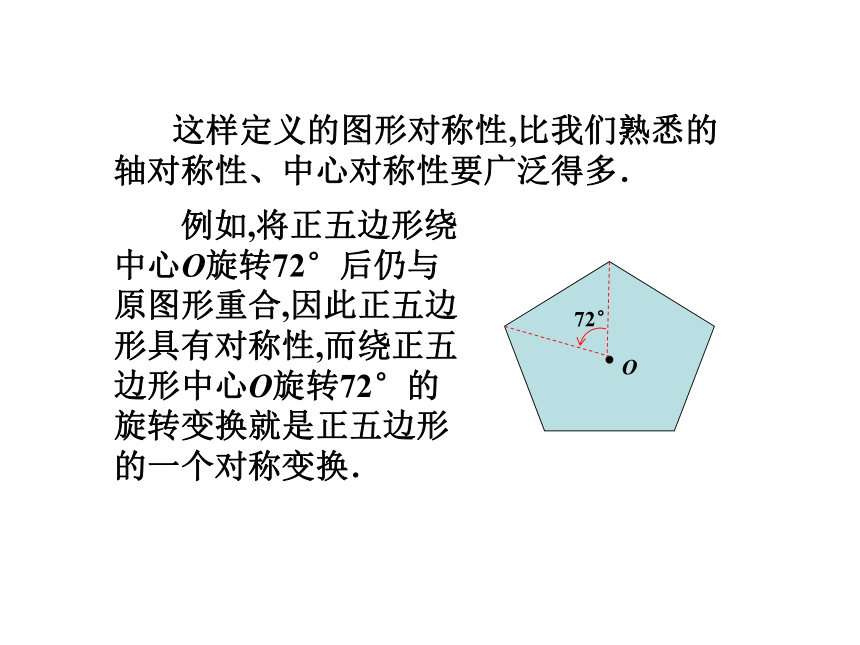
这样定义的图形对称性,比我们熟悉的轴对称性、中心对称性要广泛得多.
例如,将正五边形绕中心O旋转72°后仍与原图形重合,因此正五边形具有对称性,而绕正五边形中心O旋转72°的旋转变换就是正五边形的一个对称变换.
72°
O
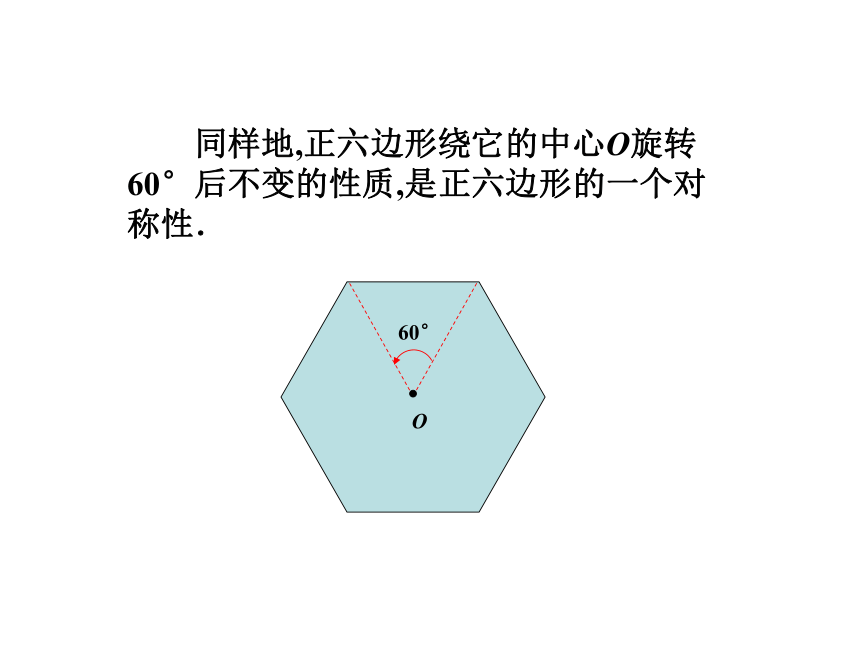
同样地,正六边形绕它的中心O旋转60°后不变的性质,是正六边形的一个对称性.
60°
O
对于一个具有对称性的平面图形,例如正多边形,它的对称变换是唯一的吗?如果不唯一,你能找出它的所有对称变换吗?
下面我们先考察一下正三角形的对称变换.
如右图,画一个三角形,在它的三个顶点上标上数字1,2,3,并画出它的三条对称轴r1,r2,r3和中心O.
1
2
3
r3
r1
r2
O
通过实验,容易发现,正三角形在下列平面刚体运动的作用下保持不变.
(1)恒等变换,记作I;
1(1?)
2(2?)
3(3?)
(2)关于对称轴r1所在直线的反射,记作r1;
1(1?)
2(3?)
3(2?)
(3)关于对称轴r2所在直线的反射,记作r2;
1(3?)
2(2?)
3(1?)
(4)关于对称轴r3所在直线的反射,记作r3;
1(2?)
2(1?)
3(3?)
(5)以O为中心转120°的旋转,记作ρ1;
1(3?)
2(1?)
3(2?)
120°
(6)以O为中心转240°的旋转,记作ρ2;
O
1(2?)
2(3?)
3(1?)
240°
在上述变换中1,2,3表示三角形123的顶点在变换下的象所在的位置.例如,对于(2)中的变换r1,我们有
1?=r(1),2?=r(2),3?=r(3).
这样,我们就找到了三角形的6个对称变换.习惯上,把它们组成的集合记作D3,即
D3={I,r1,r2,r3,ρ1,ρ2}.
为了进一步熟悉正多边形的对称变换,下面,我们再来看一下正方形有哪几个对称变换.与正三角形类似,正方形的对称变换都以其中心O为不动点,因此只要在以O为中心的旋转和关于经过O点的直线的反射中寻找就够了.
可以发现,在这6个变化中,中心O都保持不动;在D3中任意一个变换的作用下,三角形的顶点仍然是顶点.
如下图,在纸上画一个正方形,在它的4个顶点上标上数字,1,2,3,4,再画出它的4条对称轴r1,r2,r3,r4.
r3
r2
r1
r4
1
2
3
4
O
通过操作,我们可以找到下列正方形的对称变换.
(1)恒等变换,记作I;
(2)关于对称轴r1所在直线的反射,记作r1;
(3)关于对称轴r2所在直线的反射,记作r2;
(4)关于对称轴r3所在直线的反射,记作r3;
(5)关于对称轴r4所在直线的反射,记作r4;
(6)以点O为中心转90°的旋转,记作ρ1;
(7)以点O为中心转180°的旋转,记作ρ2;
(8)以点O为中心转270°的旋转,记作ρ3.
这样,我们就找到了正方形的8个对称变换,这8个对称变换都保持正方形的中心不动,而把它的顶点仍然映成顶点.习惯上,把这8个对称变换组成的集合记作D4,即
D4={I,r1,r2,r3,r4, ρ1, ρ2, ρ3}.
上面我们以正三角形、正方形为例,讨论了正多边形的对称变换.像研究数的性质时要考察数的运算一样,我们想探索的是,对于一个正多边形的对称变换的集合,其中的元素是否也可以“运算”呢?
所谓一个正多边形的两个对称变换的合成,是指先做一个对称变换,再做一个对称变换.以正方形的对称变换的合成为例,先对正方形做变换r4,再做变换ρ1,用图形表示为:
1
2
3
4
r4
ρ1
2
1
3
4
4
3
2
1
这样,我们就得到了正方形的一个新的变换,记作ρ1 r4,它对正方形的作用效果是:
1
2
3
4
4
3
2
1
ρ1 r4
我们熟悉的数字的乘法按从左到右的顺序进行,而对称变换的合成习惯上按从右到左的顺序进行.
我们发现,ρ1 r4把顶点1,2,3,4依次映到了3,2,1,4;而r1也把1,2,3,4依次映到了3,2,1,4.由于正方形的对称变换由其(任意)两个顶点所唯一确定,所以ρ1 r4与r1是相同的对称变换,即
ρ1 r4 = r1
也就是说,ρ1与r4的合成仍然是正方形的一个对称变换,而且仍然在D4中.
一般地,由对称变换的定义可以知道,一个平面图形的两个对称变换a和b的合成(即先做变换a,再做变换b)仍然是这个平面图形的一个对称变换,记作
b a.
例 对于D3,分别求:
(1) I r1;(2)r1 I;(3)r3 r2;
(4)r2 r3;(5)r2 ρ1;(6)ρ1 r2.
分析:我们只要根据对称变换合成的过程,分步骤完成两个变换即可.
解:(1)因为
1
2
3
1
3
2
1
3
2
r1
I
I r1
所以 I r1= r1.
(2)因为
1
2
3
1
3
2
1
3
2
r1
r1 I
所以 r1 I = r1.
I
(3)因为
1
2
3
1
3
2
1
3
2
r3
r3 r2
所以 r3 r2 =ρ2 .
r2
(4)因为
1
2
3
1
3
2
1
3
2
r2
r2 r3
所以 r2 r3 =ρ1 .
r3
(5)因为
1
2
3
1
3
2
1
3
2
r2
r2 ρ1
所以 r2 ρ1= r3.
ρ1
(6)因为
1
2
3
1
3
2
1
3
2
r2
ρ1 r2
所以ρ1 r2 = r1.
ρ1
数的乘法满足交换律,对称变换的合成满足交换律吗?
我们以最简单的正三角形的对称变换为例,看一看对称变换的合成是否满足交换律.
若对正三角形123先做恒等变换I,再做变换r2,即
1
2
3
1
3
2
1
3
2
r2
r2 I
I
我们发现所以 r2 I = r2.
反过来,先做变换r2,再做恒等变换I,即
1
2
3
3
2
1
3
2
1
r2
I
I r2
这时有 I r2= r2.于是我们有
r2 I=I r2
可以发现,对于任意对称变换a与恒等变换I,都有a I=I a成立。但是,对于集合D3中的其他变换,交换律并不一定成立。例如,从上面的例子中我们可以发现,r3 r2≠r2 r3.
一般地,平面图形的对称变换的合成不满足交换律.
数的乘法满足结合律,对称变换的合成满足结合律吗?
我们以正方形的对称变换为例。先对正方形1234做变换(ρ2 ρ1),再做变换ρ3,则
1
2
3
4
4
1
2
3
3
4
2
1
3
4
2
1
ρ1
ρ3
ρ2
ρ2 ρ1=ρ3
ρ3 ρ3=ρ3
于是我们得到ρ3 (ρ2 ρ1)=ρ3
若先对正方形做变换ρ1,再做变换(ρ3 ρ2),那么
1
2
3
4
1
2
3
4
1
2
3
4
ρ1
ρ3 ρ2
(ρ3 ρ2)ρ1
这时我们也得到(ρ3 ρ2 ) ρ1=ρ3.
所以 ρ3 (ρ2 ρ1) =(ρ3 ρ2 ) ρ1
从上面的讨论,我们已经看到, ρ3 (ρ2 ρ1)和 (ρ3 ρ2 ) ρ1对一个图形或一个点的作用都是对它先施行ρ1 ,再施行ρ2 ,最后再施行ρ3 ,因而ρ3 (ρ2 ρ1)和(ρ3 ρ2 ) ρ1完全一样的.
一般地,我们有:若m1,m2,m3是平面图形的3个对称变换,它们之间的合成满足结合律,即
m3 (m2 m1)=(m3 m2) m1.
我们知道,互为倒数的两数之积等于1;对数函数与指数函数互为反函数.对称变换是否也可以讨论类似的问题呢?
下面我们还是以正三角形的对称变换为例,来考察一下这个问题.对正三角形123先做变换ρ2,再做变换ρ1,我们有ρ1 ρ2=I
1
2
3
2
2
3
3
1
1
ρ2
ρ1
ρ1 ρ2
如果对正三角形先做变换ρ1,再做变换ρ2,仍然有ρ2 ρ1=I.
1
2
3
2
3
3
1
1
2
ρ1
ρ2
ρ2 ρ1
因此我们有ρ1 ρ2=ρ2 ρ1=I
一般地,如果一个对称变换a与另一个对称变换b的合成等于恒等变换I,即
b a=a b=I,
我们就称b为a的逆变换(或a为b的逆变换),记作
a-1=b(或b-1=a).
我们已经知道,两个对称变换a,b的合成 b a仍然是一个对称变换.那么,这个对称变换的逆变换又是怎样的呢?由对称变换满足结合律,我们得到
(a-1 b-1)(b a)=a-1 (b-1 b) a
=a-1 I a
=a-1 a
=I.
因此,b a的逆变换是对称变换a-1 b-1.
对称变换的定义;
正多边形的对称变换;
对称变换的合成;
对称变换的性质;
对称变换的逆变换.
回顾旧知
从上一节的讨论发现,我们可以利用平面刚体运动来定义平面图形的对称性.
例如,由于等腰三角形在关于其对称轴l的反射变换r的作用下,仍与原来的图形重合,我们就称等腰三角形具有轴对称性,并把反射变换r叫做等腰三角形的对称变换.
A
B(C)
C(B)
l
动动脑
如何定义下面的平面刚体运动?
将一个正五边形旋转72°.
72°
O
准确掌握对称变换的概念.
掌握对称变换的合成和其性质.
了解对称变换的逆变换.
【知识与能力】
通过观察、操作,了解平面图形“对称”的概念推广过程.
进一步了解对称变换的特点.
通过实例来简绍对称变换的合成、性质和逆变换.
【过程与方法】
让学生从实例中体会数学概念的导出.
对大量的实例进行观察,得出规律.
培养合作交流意识.
【情感态度与价值观】
对称变换的定义、性质
对称变换的合成、逆变换
若一个平面图形K在平面刚体运动m的作用下仍与原来的图形重合,就称K具有对称性,m叫做K的对称变换.
按照上述定义,“一个平面图形是对称图形”等价于说“一个平面图形有对称变换”.
显然,任意图形都在恒等变换下变到自身,这时我们也认为这个图形具有对称性.
这样定义的图形对称性,比我们熟悉的轴对称性、中心对称性要广泛得多.
例如,将正五边形绕中心O旋转72°后仍与原图形重合,因此正五边形具有对称性,而绕正五边形中心O旋转72°的旋转变换就是正五边形的一个对称变换.
72°
O
同样地,正六边形绕它的中心O旋转60°后不变的性质,是正六边形的一个对称性.
60°
O
对于一个具有对称性的平面图形,例如正多边形,它的对称变换是唯一的吗?如果不唯一,你能找出它的所有对称变换吗?
下面我们先考察一下正三角形的对称变换.
如右图,画一个三角形,在它的三个顶点上标上数字1,2,3,并画出它的三条对称轴r1,r2,r3和中心O.
1
2
3
r3
r1
r2
O
通过实验,容易发现,正三角形在下列平面刚体运动的作用下保持不变.
(1)恒等变换,记作I;
1(1?)
2(2?)
3(3?)
(2)关于对称轴r1所在直线的反射,记作r1;
1(1?)
2(3?)
3(2?)
(3)关于对称轴r2所在直线的反射,记作r2;
1(3?)
2(2?)
3(1?)
(4)关于对称轴r3所在直线的反射,记作r3;
1(2?)
2(1?)
3(3?)
(5)以O为中心转120°的旋转,记作ρ1;
1(3?)
2(1?)
3(2?)
120°
(6)以O为中心转240°的旋转,记作ρ2;
O
1(2?)
2(3?)
3(1?)
240°
在上述变换中1,2,3表示三角形123的顶点在变换下的象所在的位置.例如,对于(2)中的变换r1,我们有
1?=r(1),2?=r(2),3?=r(3).
这样,我们就找到了三角形的6个对称变换.习惯上,把它们组成的集合记作D3,即
D3={I,r1,r2,r3,ρ1,ρ2}.
为了进一步熟悉正多边形的对称变换,下面,我们再来看一下正方形有哪几个对称变换.与正三角形类似,正方形的对称变换都以其中心O为不动点,因此只要在以O为中心的旋转和关于经过O点的直线的反射中寻找就够了.
可以发现,在这6个变化中,中心O都保持不动;在D3中任意一个变换的作用下,三角形的顶点仍然是顶点.
如下图,在纸上画一个正方形,在它的4个顶点上标上数字,1,2,3,4,再画出它的4条对称轴r1,r2,r3,r4.
r3
r2
r1
r4
1
2
3
4
O
通过操作,我们可以找到下列正方形的对称变换.
(1)恒等变换,记作I;
(2)关于对称轴r1所在直线的反射,记作r1;
(3)关于对称轴r2所在直线的反射,记作r2;
(4)关于对称轴r3所在直线的反射,记作r3;
(5)关于对称轴r4所在直线的反射,记作r4;
(6)以点O为中心转90°的旋转,记作ρ1;
(7)以点O为中心转180°的旋转,记作ρ2;
(8)以点O为中心转270°的旋转,记作ρ3.
这样,我们就找到了正方形的8个对称变换,这8个对称变换都保持正方形的中心不动,而把它的顶点仍然映成顶点.习惯上,把这8个对称变换组成的集合记作D4,即
D4={I,r1,r2,r3,r4, ρ1, ρ2, ρ3}.
上面我们以正三角形、正方形为例,讨论了正多边形的对称变换.像研究数的性质时要考察数的运算一样,我们想探索的是,对于一个正多边形的对称变换的集合,其中的元素是否也可以“运算”呢?
所谓一个正多边形的两个对称变换的合成,是指先做一个对称变换,再做一个对称变换.以正方形的对称变换的合成为例,先对正方形做变换r4,再做变换ρ1,用图形表示为:
1
2
3
4
r4
ρ1
2
1
3
4
4
3
2
1
这样,我们就得到了正方形的一个新的变换,记作ρ1 r4,它对正方形的作用效果是:
1
2
3
4
4
3
2
1
ρ1 r4
我们熟悉的数字的乘法按从左到右的顺序进行,而对称变换的合成习惯上按从右到左的顺序进行.
我们发现,ρ1 r4把顶点1,2,3,4依次映到了3,2,1,4;而r1也把1,2,3,4依次映到了3,2,1,4.由于正方形的对称变换由其(任意)两个顶点所唯一确定,所以ρ1 r4与r1是相同的对称变换,即
ρ1 r4 = r1
也就是说,ρ1与r4的合成仍然是正方形的一个对称变换,而且仍然在D4中.
一般地,由对称变换的定义可以知道,一个平面图形的两个对称变换a和b的合成(即先做变换a,再做变换b)仍然是这个平面图形的一个对称变换,记作
b a.
例 对于D3,分别求:
(1) I r1;(2)r1 I;(3)r3 r2;
(4)r2 r3;(5)r2 ρ1;(6)ρ1 r2.
分析:我们只要根据对称变换合成的过程,分步骤完成两个变换即可.
解:(1)因为
1
2
3
1
3
2
1
3
2
r1
I
I r1
所以 I r1= r1.
(2)因为
1
2
3
1
3
2
1
3
2
r1
r1 I
所以 r1 I = r1.
I
(3)因为
1
2
3
1
3
2
1
3
2
r3
r3 r2
所以 r3 r2 =ρ2 .
r2
(4)因为
1
2
3
1
3
2
1
3
2
r2
r2 r3
所以 r2 r3 =ρ1 .
r3
(5)因为
1
2
3
1
3
2
1
3
2
r2
r2 ρ1
所以 r2 ρ1= r3.
ρ1
(6)因为
1
2
3
1
3
2
1
3
2
r2
ρ1 r2
所以ρ1 r2 = r1.
ρ1
数的乘法满足交换律,对称变换的合成满足交换律吗?
我们以最简单的正三角形的对称变换为例,看一看对称变换的合成是否满足交换律.
若对正三角形123先做恒等变换I,再做变换r2,即
1
2
3
1
3
2
1
3
2
r2
r2 I
I
我们发现所以 r2 I = r2.
反过来,先做变换r2,再做恒等变换I,即
1
2
3
3
2
1
3
2
1
r2
I
I r2
这时有 I r2= r2.于是我们有
r2 I=I r2
可以发现,对于任意对称变换a与恒等变换I,都有a I=I a成立。但是,对于集合D3中的其他变换,交换律并不一定成立。例如,从上面的例子中我们可以发现,r3 r2≠r2 r3.
一般地,平面图形的对称变换的合成不满足交换律.
数的乘法满足结合律,对称变换的合成满足结合律吗?
我们以正方形的对称变换为例。先对正方形1234做变换(ρ2 ρ1),再做变换ρ3,则
1
2
3
4
4
1
2
3
3
4
2
1
3
4
2
1
ρ1
ρ3
ρ2
ρ2 ρ1=ρ3
ρ3 ρ3=ρ3
于是我们得到ρ3 (ρ2 ρ1)=ρ3
若先对正方形做变换ρ1,再做变换(ρ3 ρ2),那么
1
2
3
4
1
2
3
4
1
2
3
4
ρ1
ρ3 ρ2
(ρ3 ρ2)ρ1
这时我们也得到(ρ3 ρ2 ) ρ1=ρ3.
所以 ρ3 (ρ2 ρ1) =(ρ3 ρ2 ) ρ1
从上面的讨论,我们已经看到, ρ3 (ρ2 ρ1)和 (ρ3 ρ2 ) ρ1对一个图形或一个点的作用都是对它先施行ρ1 ,再施行ρ2 ,最后再施行ρ3 ,因而ρ3 (ρ2 ρ1)和(ρ3 ρ2 ) ρ1完全一样的.
一般地,我们有:若m1,m2,m3是平面图形的3个对称变换,它们之间的合成满足结合律,即
m3 (m2 m1)=(m3 m2) m1.
我们知道,互为倒数的两数之积等于1;对数函数与指数函数互为反函数.对称变换是否也可以讨论类似的问题呢?
下面我们还是以正三角形的对称变换为例,来考察一下这个问题.对正三角形123先做变换ρ2,再做变换ρ1,我们有ρ1 ρ2=I
1
2
3
2
2
3
3
1
1
ρ2
ρ1
ρ1 ρ2
如果对正三角形先做变换ρ1,再做变换ρ2,仍然有ρ2 ρ1=I.
1
2
3
2
3
3
1
1
2
ρ1
ρ2
ρ2 ρ1
因此我们有ρ1 ρ2=ρ2 ρ1=I
一般地,如果一个对称变换a与另一个对称变换b的合成等于恒等变换I,即
b a=a b=I,
我们就称b为a的逆变换(或a为b的逆变换),记作
a-1=b(或b-1=a).
我们已经知道,两个对称变换a,b的合成 b a仍然是一个对称变换.那么,这个对称变换的逆变换又是怎样的呢?由对称变换满足结合律,我们得到
(a-1 b-1)(b a)=a-1 (b-1 b) a
=a-1 I a
=a-1 a
=I.
因此,b a的逆变换是对称变换a-1 b-1.
对称变换的定义;
正多边形的对称变换;
对称变换的合成;
对称变换的性质;
对称变换的逆变换.
