华东师大版九年级数学下册 27.1.3 圆周角 同步练习含答案
文档属性
| 名称 | 华东师大版九年级数学下册 27.1.3 圆周角 同步练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览


文档简介
第27章 圆 27.1.3 圆周角 同步练习题
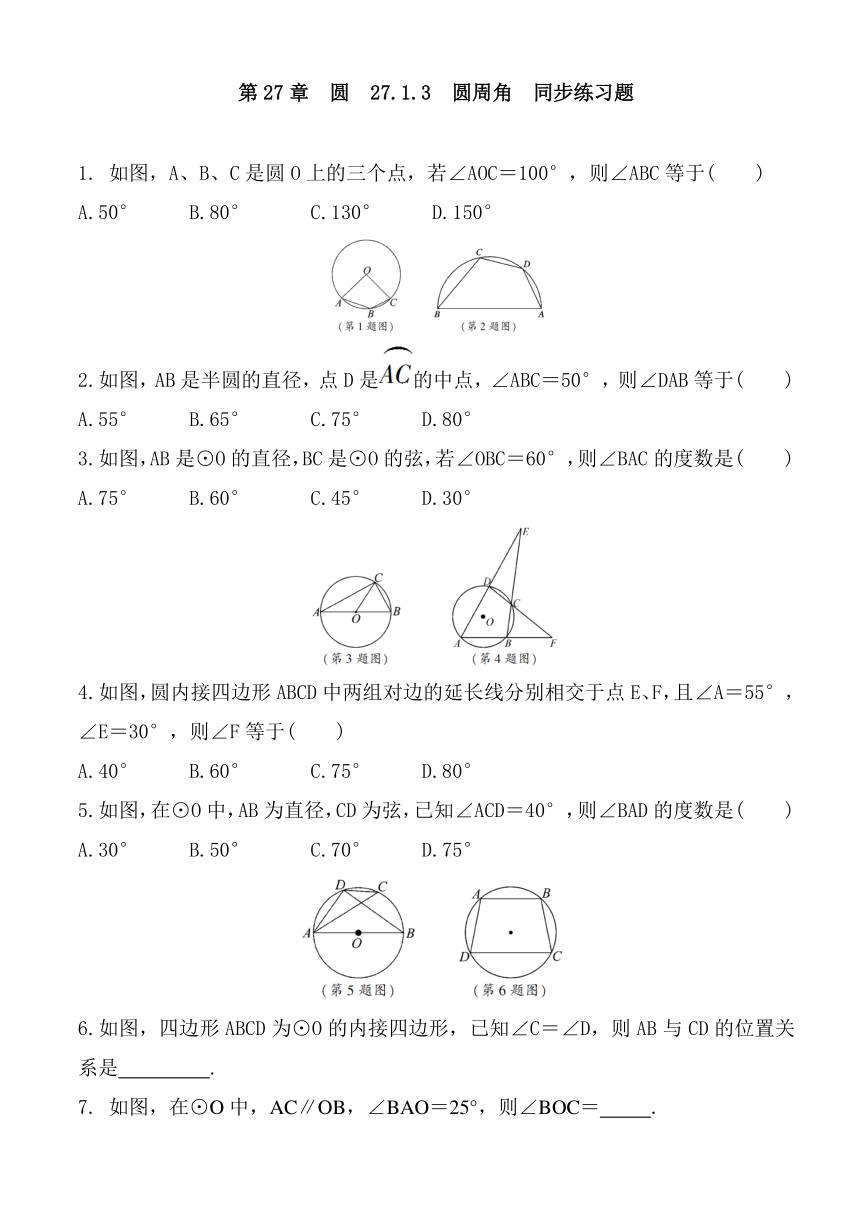
1. 如图,A、B、C是圆O上的三个点,若∠AOC=100°,则∠ABC等于( )
A.50° B.80° C.130° D.150°
2.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55° B.65° C.75° D.80°
3.如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
4.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E、F,且∠A=55°,∠E=30°,则∠F等于( )
A.40° B.60° C.75° D.80°
5.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数是( )
A.30° B.50° C.70° D.75°
6.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是 .
7. 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC= .
8. 如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB= .
9. 如图,⊙O是△ABC的外接圆,∠C=30°,AB=4cm,则⊙O的半径为________cm.
10. 如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为 .
11. 如图,在圆内接四边形ABCD中,∠D=150°,则 ∠B=________.
12. 如图,A,B,C是⊙O上的三点,∠AOC=150°则∠B的度数是________.
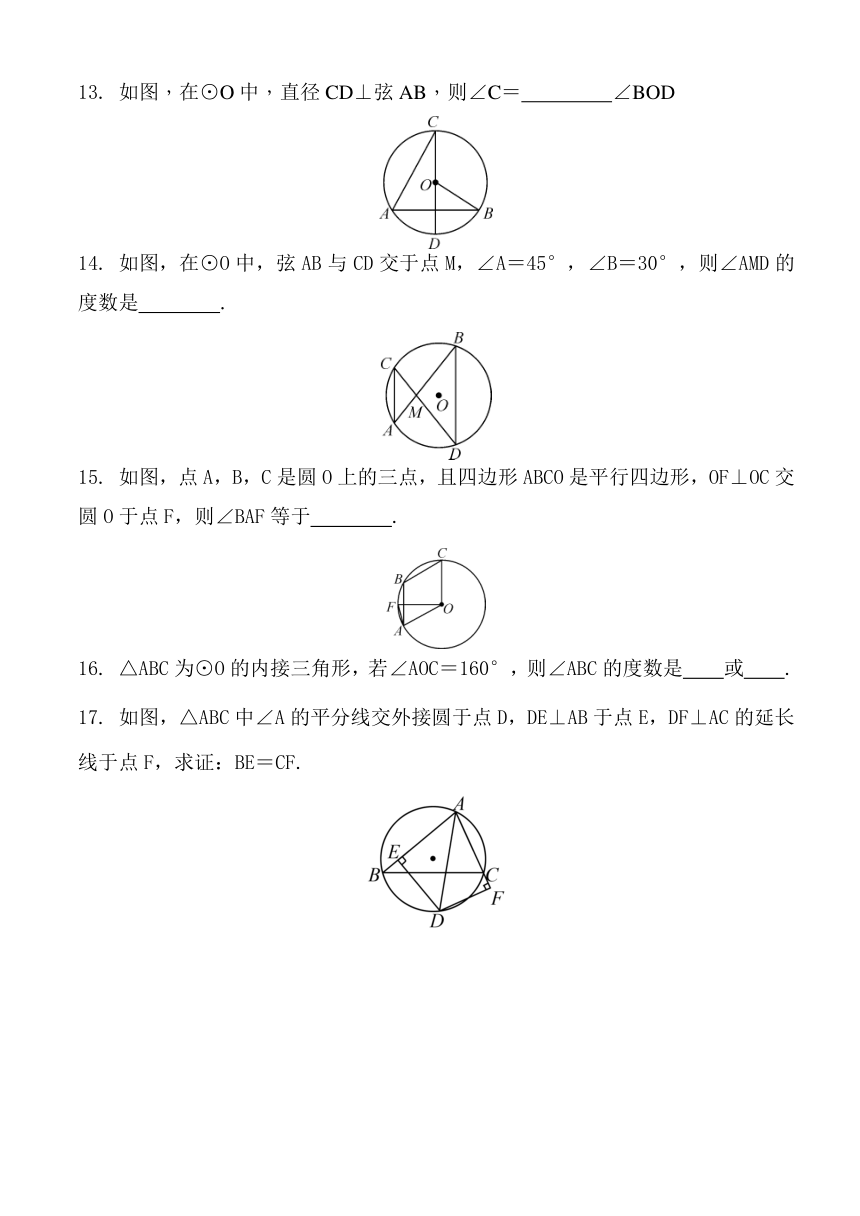
13. 如图,在⊙O中,直径CD⊥弦AB,则∠C= ∠BOD
14. 如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠B=30°,则∠AMD的度数是 .
15. 如图,点A,B,C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于 .
16. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是 或 .
17. 如图,△ABC中∠A的平分线交外接圆于点D,DE⊥AB于点E,DF⊥AC的延长线于点F,求证:BE=CF.
18. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是CAD上一点(不与C,D重合),求证:∠CPD=∠COB.
(2)点P′在上(不与C,D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
19. 如图,等边△ABC内接于⊙O,P是弧AB上任意一点(点P不与点A,B重合),连接PA,PB,PC,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC=_______度,∠BPC=________度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积.
答案:
1—5 CBDAB
6. AB∥CD
7. 50°
8. 90°
9. 4
10. 40°
11. 30°
12. 75°
13.
14. 75°
15. 15°
16. 80° 100°
17. 证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,连接BD,CD,
则BD=CD,∴△BED≌△CFD,∴BE=CF
18. 解:(1)连接OD,∵AB为直径,AB⊥CD(弦),∴=,∠BOC=∠COD.又∠CPD=∠COD,∴∠COB=∠CPD
(2)∠CP′D+∠COB=180°,证明:∵P,C,P′,D四点共圆,
∴∠CPD+∠CP′D=180°,又∵∠CPD=∠COB,∴∠COB+∠CP′D=180°
19. (1) 60 60
解:(2)∵CM∥BP,∴∠MCP=∠BPC=60°,在△MPC中,∠MPC=60°,
∴∠M=60°,易得∠BCP=∠ACM,由∠M=∠BPC,∠ACM=∠BCP,AC=BC
得△ACM≌△BCP(AAS)
(3)∵△ACM≌△BCP,∴CM=CP,AM=BP,又∠M=60°,∴△PCM为等边三角形,∴CM=CP=PM=1+2=3.作PH⊥CM于H,在Rt△PMH中,∠MPH=30°,∴PH=,∴S四边形PBCM=(PB+CM)×PH=(2+3)×=
1. 如图,A、B、C是圆O上的三个点,若∠AOC=100°,则∠ABC等于( )
A.50° B.80° C.130° D.150°
2.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55° B.65° C.75° D.80°
3.如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
4.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E、F,且∠A=55°,∠E=30°,则∠F等于( )
A.40° B.60° C.75° D.80°
5.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数是( )
A.30° B.50° C.70° D.75°
6.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是 .
7. 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC= .
8. 如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB= .
9. 如图,⊙O是△ABC的外接圆,∠C=30°,AB=4cm,则⊙O的半径为________cm.
10. 如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为 .
11. 如图,在圆内接四边形ABCD中,∠D=150°,则 ∠B=________.
12. 如图,A,B,C是⊙O上的三点,∠AOC=150°则∠B的度数是________.
13. 如图,在⊙O中,直径CD⊥弦AB,则∠C= ∠BOD
14. 如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠B=30°,则∠AMD的度数是 .
15. 如图,点A,B,C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于 .
16. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是 或 .
17. 如图,△ABC中∠A的平分线交外接圆于点D,DE⊥AB于点E,DF⊥AC的延长线于点F,求证:BE=CF.
18. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是CAD上一点(不与C,D重合),求证:∠CPD=∠COB.
(2)点P′在上(不与C,D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
19. 如图,等边△ABC内接于⊙O,P是弧AB上任意一点(点P不与点A,B重合),连接PA,PB,PC,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC=_______度,∠BPC=________度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积.
答案:
1—5 CBDAB
6. AB∥CD
7. 50°
8. 90°
9. 4
10. 40°
11. 30°
12. 75°
13.
14. 75°
15. 15°
16. 80° 100°
17. 证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,连接BD,CD,
则BD=CD,∴△BED≌△CFD,∴BE=CF
18. 解:(1)连接OD,∵AB为直径,AB⊥CD(弦),∴=,∠BOC=∠COD.又∠CPD=∠COD,∴∠COB=∠CPD
(2)∠CP′D+∠COB=180°,证明:∵P,C,P′,D四点共圆,
∴∠CPD+∠CP′D=180°,又∵∠CPD=∠COB,∴∠COB+∠CP′D=180°
19. (1) 60 60
解:(2)∵CM∥BP,∴∠MCP=∠BPC=60°,在△MPC中,∠MPC=60°,
∴∠M=60°,易得∠BCP=∠ACM,由∠M=∠BPC,∠ACM=∠BCP,AC=BC
得△ACM≌△BCP(AAS)
(3)∵△ACM≌△BCP,∴CM=CP,AM=BP,又∠M=60°,∴△PCM为等边三角形,∴CM=CP=PM=1+2=3.作PH⊥CM于H,在Rt△PMH中,∠MPH=30°,∴PH=,∴S四边形PBCM=(PB+CM)×PH=(2+3)×=
