人教版八年级数学下册17.2 勾股定理的逆定理(勾股定理逆定理的证明)(课件)(共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.2 勾股定理的逆定理(勾股定理逆定理的证明)(课件)(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 778.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 16:14:04 | ||
图片预览




文档简介
(共21张PPT)
人教版
数学八年级下册
第十七章
勾股定理
17.2
勾股定理的逆定理(勾股定理逆定理的证明)
前言
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.了解命题的逆命题,定理逆定理以及它们之间的关系。
重点
勾股定理逆定理的理解。
难点
勾股定理逆定理的证明。
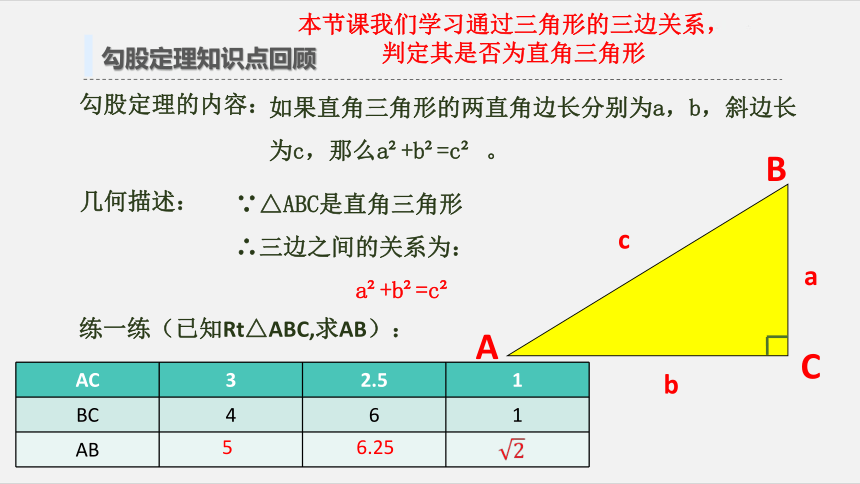
AC
3
2.5
1
BC
4
6
1
AB
勾股定理知识点回顾
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c
。
b
a
c
A
B
C
∵△ABC是直角三角形
∴三边之间的关系为:
a +b =c
勾股定理的内容:
几何描述:
练一练(已知Rt△ABC,求AB):
5
6.25
本节课我们学习通过三角形的三边关系,
判定其是否为直角三角形
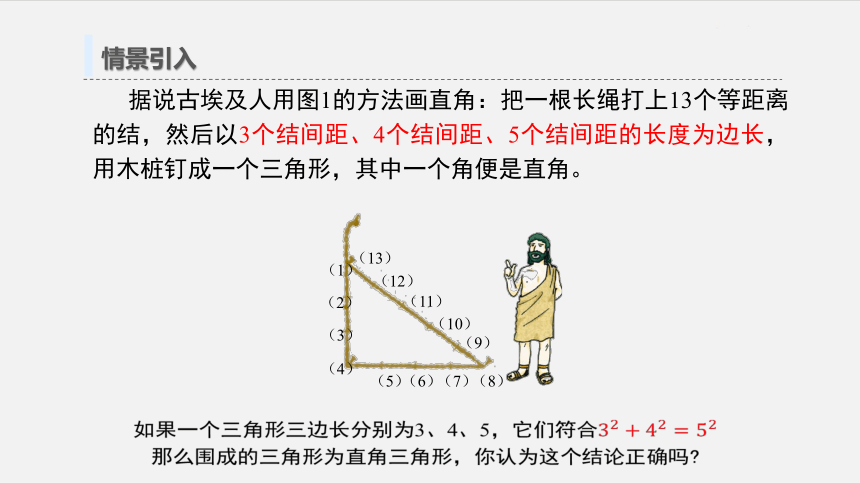
情景引入
据说古埃及人用图1的方法画直角:把一根长绳打上13个等距离的结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
如果一个三角形三边长分别为3、4、5,它们符合
那么围成的三角形为直角三角形,你认为这个结论正确吗
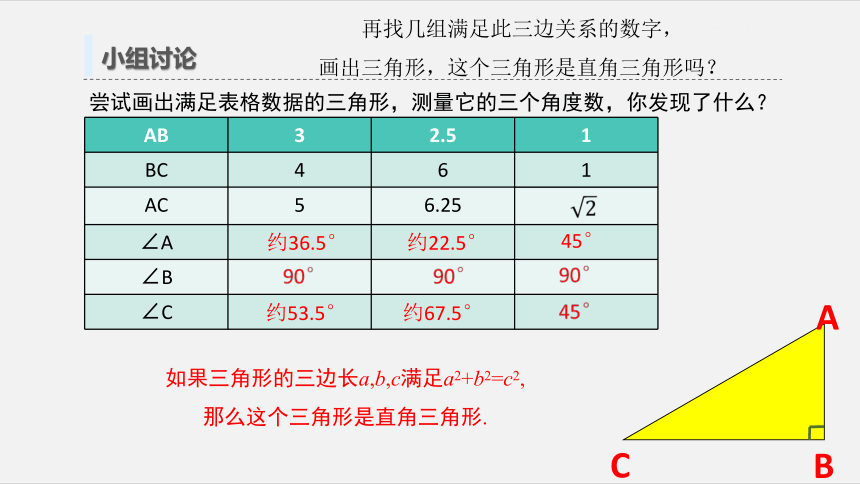
小组讨论
AB
3
2.5
1
BC
4
6
1
AC
5
6.25
∠A
∠B
∠C
A
B
C
尝试画出满足表格数据的三角形,测量它的三个角度数,你发现了什么?
约36.5°
约22.5°
45°
约53.5°
约67.5°
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
再找几组满足此三边关系的数字,
画出三角形,这个三角形是直角三角形吗?
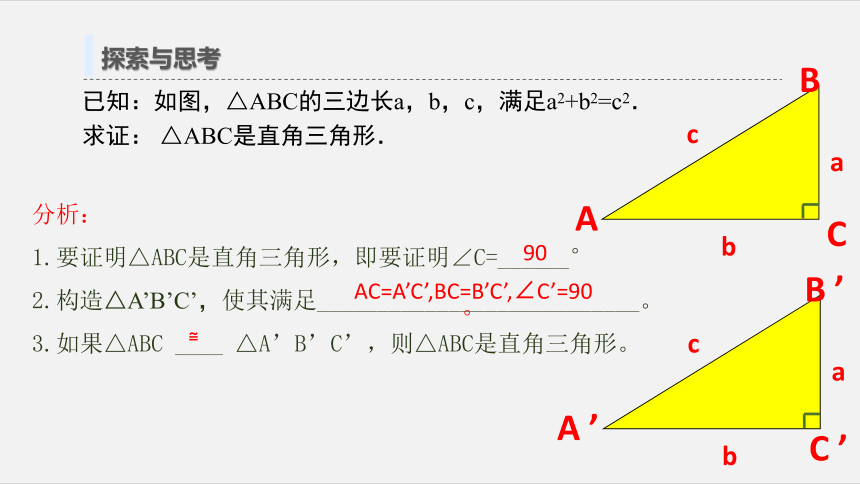
探索与思考
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:
△ABC是直角三角形.
分析:
1.要证明△ABC是直角三角形,即要证明∠C=______°
2.构造△A’B’C’,使其满足___________________________。
3.如果△ABC
____
△A’B’C’,则△ABC是直角三角形。
90
≌
AC=A’C’,BC=B’C’,∠C’=90°
b
a
c
A
B
C
b
a
c
A
’
B
’
C
’
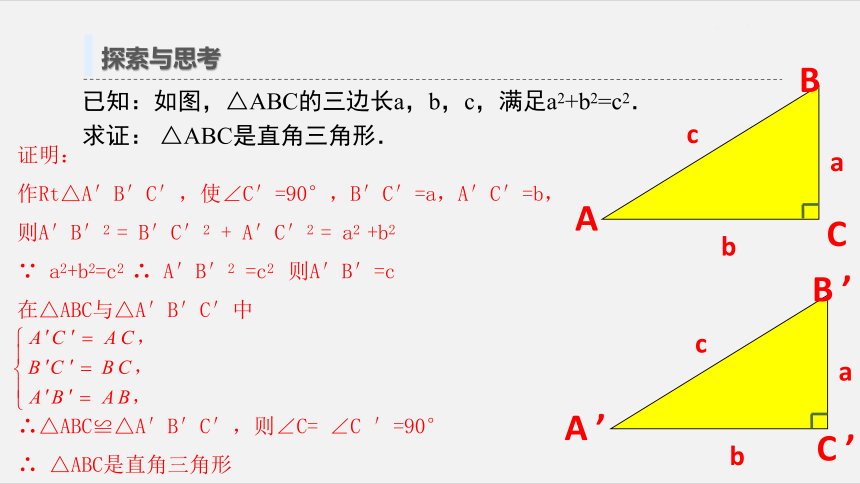
探索与思考
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:
△ABC是直角三角形.
证明:
作Rt△A′B′C′,使∠C′=90°,B′C′=a,A′C′=b,
则A′B′2
=
B′C′2
+
A′C′2
=
a2
+b2
∵
a2+b2=c2
∴
A′B′2
=c2
则A′B′=c
在△ABC与△A′B′C′中
∴△ABC≌△A′B′C′,则∠C=
∠C
′=90°
∴
△ABC是直角三角形
b
a
c
A
B
C
b
a
c
A
’
B
’
C
’
勾股定理的逆定理
如果三角形的三边长a
,b
,c满足
a2+b2=c2,那么这个三角形是直角三角形。
几何描述:
∵三角形三边之间的关系为:a +b =c
∴△ABC是直角三角形
勾股数的概念:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数。
勾股数的性质:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数。
b
a
c
A
B
C
判断直角三角形的方法
用角判断:
1.两个锐角互余
的三角形是直角三角形;
2.有一个角是90°的三角形是直角三角形;
用边判断:
如果已知条件与边有关,则可通过勾股定理的逆定理(a +b =c )进行判断.
练一练
下面以a,b,c为边长的三角形是不是直角三角形?
1、a=15
,b=8
,c=17
2、a=13
,b=14
,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
小结
运用勾股定理的逆定理判断直角三角形的一般步骤:
1.找:确定三角形的最长边。
2.算:分别计算出最长边的平方与另两边的平方和。
3.比:通过比较来判断最长边的平方与另两边的平方和是否相等。
4.判:作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形。
互逆命题与互逆定理
观察下面的两个命题,你发现了什么?
命题1
如果直角三角形的两条直角边长分别为a,b,斜边为c,
那么a2+b2=c2。
命题2
如果三角形的三边长a
、b
、c满足a2+b2=c2,
那么这个三角形是直角三角形。
它们是题设和结论正好相反两个命题
小结
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理。勾股定理与勾股定理的逆定理为互逆定理。
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题。
练一练
说出下列命题的逆命题,这些逆命题成立吗?
(1)两条直线平行,内错角相等。
(2)如果两个实数的绝对值相等,那么这两个实数的平方相等。
(3)对顶角相等。
(4)在角的内部,到角的两边距离相等的点在角的平分线上。
随堂测试
1.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5
B.a:b:c=7:24:25
C.a2=b2﹣c2
D.∠A=∠C﹣∠B
【答案】A
【详解】解:A、∵∠A:∠B:∠C=3:4:5,∴∠C=×180°=75°,
故不能判定△ABC是直角三角形;
B、∵72+242=252,∴△ABC为直角三角形;
C、∵a2=b2﹣c2,∴b2=c2+a2,故△ABC为直角三角形;
D、∵∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,∴∠C=90°,故△ABC为直角三角形.故选:A.
随堂测试
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.
B.1,
C.6,7,8
D.2,3,4
3.下列由线段a、b、c组成的三角形是直角三角形的是(
)
A.a=1,
b=2,
c=3;
B.a=4
,
b=5
,c=6;
C.a=9,
b=12,c=15;
D.a=13,
b=14
,c=15
随堂测试
4.满足下列条件的△ABC不是直角三角形的是(
)
A.BC=1,AC=2,AB=B.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
D.∠A:∠B:∠C=3:4:5
【答案】D
【详解】
A.∵12+()2=22,∴△ABC是直角三角形,故本选项不符合题意;
B.∵12+22=()2,∴△ABC是直角三角形,故本选项不符合题意;
C.设BC=3x,则AC=4x,AB=5x.
∵(3x)2+(4x)2=(5x)2,∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A+∠B+∠C=180°,∠A:∠B:∠C=3:4:5,∴∠A=45°,∠5=60°,∠C=75°,∴△ABC不是直角三角形,故本选项符合题意.故选D.
随堂测试
5.已知△ABC的三边分别长为a,b,c,且满足,则△ABC是(
).
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.不是直角三角形
【答案】A
【解析】
等式++=0
可化为++=0,
根据非负数的性质可得a-17=0,b-15=0,c-8=0,
所以a=17,b=15,c=8;又因,
所以△ABC是
以a为斜边的直角三角形,故选A.
随堂测试(提高)
6.一个三角形的三边长分别为13、5、12,则最长边上的高是______.
【答案】.
【详解】
∵52+122=132,
∴此三角形是直角三角形,设最长边上的高为h
cm.
S=×5×12=×13×h,解得:h=.
故答案为:.
课堂互动
Classroom
Interaction
理解勾股定理逆定理
01
课后回顾
掌握勾股定理逆定理的证明
02
互逆命题之间的关系
03
THANKS
“
”
人教版
数学八年级下册
第十七章
勾股定理
17.2
勾股定理的逆定理(勾股定理逆定理的证明)
前言
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.了解命题的逆命题,定理逆定理以及它们之间的关系。
重点
勾股定理逆定理的理解。
难点
勾股定理逆定理的证明。
AC
3
2.5
1
BC
4
6
1
AB
勾股定理知识点回顾
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c
。
b
a
c
A
B
C
∵△ABC是直角三角形
∴三边之间的关系为:
a +b =c
勾股定理的内容:
几何描述:
练一练(已知Rt△ABC,求AB):
5
6.25
本节课我们学习通过三角形的三边关系,
判定其是否为直角三角形
情景引入
据说古埃及人用图1的方法画直角:把一根长绳打上13个等距离的结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
如果一个三角形三边长分别为3、4、5,它们符合
那么围成的三角形为直角三角形,你认为这个结论正确吗
小组讨论
AB
3
2.5
1
BC
4
6
1
AC
5
6.25
∠A
∠B
∠C
A
B
C
尝试画出满足表格数据的三角形,测量它的三个角度数,你发现了什么?
约36.5°
约22.5°
45°
约53.5°
约67.5°
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
再找几组满足此三边关系的数字,
画出三角形,这个三角形是直角三角形吗?
探索与思考
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:
△ABC是直角三角形.
分析:
1.要证明△ABC是直角三角形,即要证明∠C=______°
2.构造△A’B’C’,使其满足___________________________。
3.如果△ABC
____
△A’B’C’,则△ABC是直角三角形。
90
≌
AC=A’C’,BC=B’C’,∠C’=90°
b
a
c
A
B
C
b
a
c
A
’
B
’
C
’
探索与思考
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:
△ABC是直角三角形.
证明:
作Rt△A′B′C′,使∠C′=90°,B′C′=a,A′C′=b,
则A′B′2
=
B′C′2
+
A′C′2
=
a2
+b2
∵
a2+b2=c2
∴
A′B′2
=c2
则A′B′=c
在△ABC与△A′B′C′中
∴△ABC≌△A′B′C′,则∠C=
∠C
′=90°
∴
△ABC是直角三角形
b
a
c
A
B
C
b
a
c
A
’
B
’
C
’
勾股定理的逆定理
如果三角形的三边长a
,b
,c满足
a2+b2=c2,那么这个三角形是直角三角形。
几何描述:
∵三角形三边之间的关系为:a +b =c
∴△ABC是直角三角形
勾股数的概念:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数。
勾股数的性质:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数。
b
a
c
A
B
C
判断直角三角形的方法
用角判断:
1.两个锐角互余
的三角形是直角三角形;
2.有一个角是90°的三角形是直角三角形;
用边判断:
如果已知条件与边有关,则可通过勾股定理的逆定理(a +b =c )进行判断.
练一练
下面以a,b,c为边长的三角形是不是直角三角形?
1、a=15
,b=8
,c=17
2、a=13
,b=14
,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
小结
运用勾股定理的逆定理判断直角三角形的一般步骤:
1.找:确定三角形的最长边。
2.算:分别计算出最长边的平方与另两边的平方和。
3.比:通过比较来判断最长边的平方与另两边的平方和是否相等。
4.判:作出结论,若相等,则说明这个三角形是直角三角形,否则不是直角三角形。
互逆命题与互逆定理
观察下面的两个命题,你发现了什么?
命题1
如果直角三角形的两条直角边长分别为a,b,斜边为c,
那么a2+b2=c2。
命题2
如果三角形的三边长a
、b
、c满足a2+b2=c2,
那么这个三角形是直角三角形。
它们是题设和结论正好相反两个命题
小结
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理。勾股定理与勾股定理的逆定理为互逆定理。
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题。
练一练
说出下列命题的逆命题,这些逆命题成立吗?
(1)两条直线平行,内错角相等。
(2)如果两个实数的绝对值相等,那么这两个实数的平方相等。
(3)对顶角相等。
(4)在角的内部,到角的两边距离相等的点在角的平分线上。
随堂测试
1.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5
B.a:b:c=7:24:25
C.a2=b2﹣c2
D.∠A=∠C﹣∠B
【答案】A
【详解】解:A、∵∠A:∠B:∠C=3:4:5,∴∠C=×180°=75°,
故不能判定△ABC是直角三角形;
B、∵72+242=252,∴△ABC为直角三角形;
C、∵a2=b2﹣c2,∴b2=c2+a2,故△ABC为直角三角形;
D、∵∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,∴∠C=90°,故△ABC为直角三角形.故选:A.
随堂测试
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.
B.1,
C.6,7,8
D.2,3,4
3.下列由线段a、b、c组成的三角形是直角三角形的是(
)
A.a=1,
b=2,
c=3;
B.a=4
,
b=5
,c=6;
C.a=9,
b=12,c=15;
D.a=13,
b=14
,c=15
随堂测试
4.满足下列条件的△ABC不是直角三角形的是(
)
A.BC=1,AC=2,AB=B.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
D.∠A:∠B:∠C=3:4:5
【答案】D
【详解】
A.∵12+()2=22,∴△ABC是直角三角形,故本选项不符合题意;
B.∵12+22=()2,∴△ABC是直角三角形,故本选项不符合题意;
C.设BC=3x,则AC=4x,AB=5x.
∵(3x)2+(4x)2=(5x)2,∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A+∠B+∠C=180°,∠A:∠B:∠C=3:4:5,∴∠A=45°,∠5=60°,∠C=75°,∴△ABC不是直角三角形,故本选项符合题意.故选D.
随堂测试
5.已知△ABC的三边分别长为a,b,c,且满足,则△ABC是(
).
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.不是直角三角形
【答案】A
【解析】
等式++=0
可化为++=0,
根据非负数的性质可得a-17=0,b-15=0,c-8=0,
所以a=17,b=15,c=8;又因,
所以△ABC是
以a为斜边的直角三角形,故选A.
随堂测试(提高)
6.一个三角形的三边长分别为13、5、12,则最长边上的高是______.
【答案】.
【详解】
∵52+122=132,
∴此三角形是直角三角形,设最长边上的高为h
cm.
S=×5×12=×13×h,解得:h=.
故答案为:.
课堂互动
Classroom
Interaction
理解勾股定理逆定理
01
课后回顾
掌握勾股定理逆定理的证明
02
互逆命题之间的关系
03
THANKS
“
”
