人教版八年级数学下册18.1.1 平行线的性质(对边和对角的关系)(课件)(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.1 平行线的性质(对边和对角的关系)(课件)(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 994.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
人教版
数学八年级下册
第十八章
平行四边形
18.1.1
平行线的性质(对边和对角的关系)
前言
学习目标
1.理解平行四边形的概念。
2.探索并证明平行四边形对边与对角相等。
3.利用平行四边形的性质解决实际问题。
重点
探索并证明平行四边形对边与对角相等。
难点
利用平行四边形的性质解决实际问题。
生活中常见的平行四边形
尝试一些生活中常见的平行四边形的例子
平行四边形
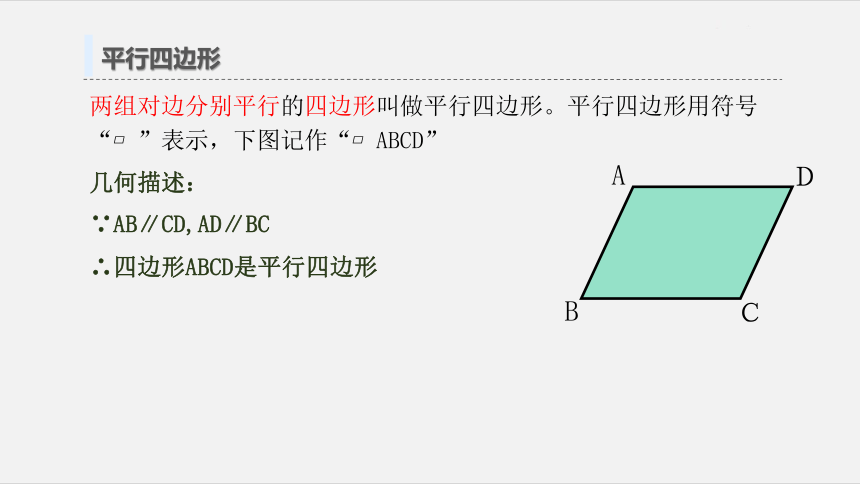
两组对边分别平行的四边形叫做平行四边形。平行四边形用符号“ ”表示,下图记作“ ABCD”
A
B
D
C
几何描述:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
探索与思考
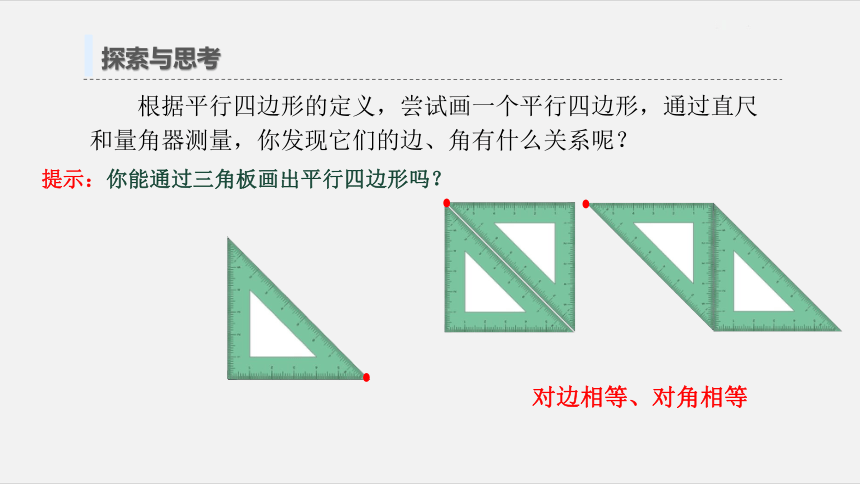
根据平行四边形的定义,尝试画一个平行四边形,通过直尺和量角器测量,你发现它们的边、角有什么关系呢?
提示:你能通过三角板画出平行四边形吗?
对边相等、对角相等
证明
A
B
D
C
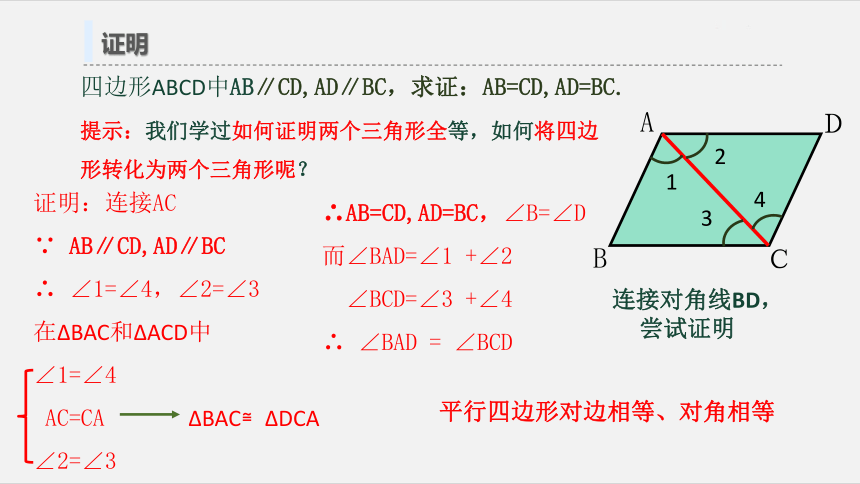
四边形ABCD中AB∥CD,AD∥BC,求证:AB=CD,AD=BC.
提示:我们学过如何证明两个三角形全等,如何将四边形转化为两个三角形呢?
1
2
3
4
证明:连接AC
∵
AB∥CD,AD∥BC
∴
∠1=∠4,∠2=∠3
在 BAC和 ACD中
∠1=∠4
AC=CA
BAC≌ DCA
∠2=∠3
∴AB=CD,AD=BC,∠B=∠D
而∠BAD=∠1
+∠2
∠BCD=∠3
+∠4
∴
∠BAD
=
∠BCD
平行四边形对边相等、对角相等
连接对角线BD,尝试证明
练一练
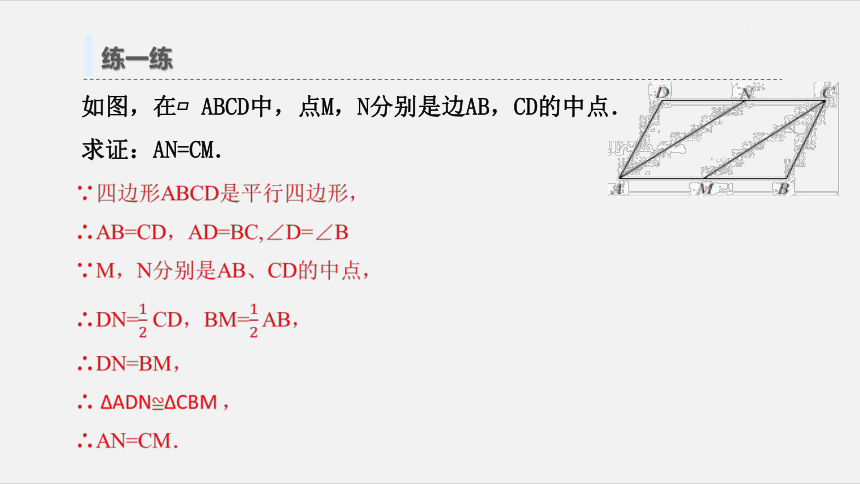
如图,在 ABCD中,点M,N分别是边AB,CD的中点.
求证:AN=CM.
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠D=∠B
∵M,N分别是AB、CD的中点,
∴DN=
CD,BM=
AB,
∴DN=BM,
∴
ADN≌ CBM
,
∴AN=CM.
探索与思考
A
B
D
C
已知 ABCD,求证:∠A与∠B,∠A与∠D之间的关系.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∠A+∠D=180°
平行四边形相邻的两个角互补
你能通过不画辅助线的方法证明平行四边形对角相等吗?
探索两条平行线之间的距离
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
H
A
B
C
D
G
b
a
∵
a
//
b,
AD
//
GH
//
BC
∴
AGHD,
ABCD,
HGBC
∴
AD
=
GH
=
BC
两条平行线之间的平行线段相等
探索两条平行线之间的距离
A
B
C
D
a
b
H
G
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
∵
DA、GH、CB垂直于
a
∴
DA
//
GH
//
CB
而a
//
b
∴
AGHD,
ABCD,
HGBC
∴
AD
=
GH
=
BC
如果两条直线平行,那么一条直线上的所有点到另一条直线的距离都相等,
即两条直线之间的距离相等。
练一练
1.如图所示中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若,,求的度数.
【详解】
(1)在平行四边形ABCD中,
BC,,
∵AE=CF,
∴
BF,
∴四边形BEDF是平行四边形
∴
(2)∵
∴∠FAD=∠AFD=70°
而AD∥BC
∴∠FAD
=∠AFB=70°
练一练
2.已知:如图,在 ABCD中,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.求证:
(1)△ABE≌△CDF;
(2)BE∥DF.
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∵∠BAC+∠BAE=∠DCA+∠DCF=180°,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF;
(2)∵△ABE≌△CDF,
∴∠E=∠F,
∴BE∥DF.
练一练
3.如图,在中,为的中点,连结并延长交的延长线于点,求证:.
【详解】
证明:四边形是平行四边形
,
,
是的中点,
,
在和中
,
,.
练一练
4.如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.
(1)用含字母a,b的代数式表示矩形中空白部分的面积;
(2)当a=3,b=2时,求矩形中空白部分的面积.
【思路】
(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;
(2)将a=3,b=2代入(1)中即可;
【详解】
(1)S=ab﹣a﹣b+1;
(2)当a=3,b=2时,S=6﹣3﹣2+1=2;
课堂互动
Classroom
Interaction
理解平行四边形的概念
01
课后回顾
理解平行四边形的性质
02
利用平行四边形的性质
解决实际问题
03
THANKS
“
”
人教版
数学八年级下册
第十八章
平行四边形
18.1.1
平行线的性质(对边和对角的关系)
前言
学习目标
1.理解平行四边形的概念。
2.探索并证明平行四边形对边与对角相等。
3.利用平行四边形的性质解决实际问题。
重点
探索并证明平行四边形对边与对角相等。
难点
利用平行四边形的性质解决实际问题。
生活中常见的平行四边形
尝试一些生活中常见的平行四边形的例子
平行四边形
两组对边分别平行的四边形叫做平行四边形。平行四边形用符号“ ”表示,下图记作“ ABCD”
A
B
D
C
几何描述:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
探索与思考
根据平行四边形的定义,尝试画一个平行四边形,通过直尺和量角器测量,你发现它们的边、角有什么关系呢?
提示:你能通过三角板画出平行四边形吗?
对边相等、对角相等
证明
A
B
D
C
四边形ABCD中AB∥CD,AD∥BC,求证:AB=CD,AD=BC.
提示:我们学过如何证明两个三角形全等,如何将四边形转化为两个三角形呢?
1
2
3
4
证明:连接AC
∵
AB∥CD,AD∥BC
∴
∠1=∠4,∠2=∠3
在 BAC和 ACD中
∠1=∠4
AC=CA
BAC≌ DCA
∠2=∠3
∴AB=CD,AD=BC,∠B=∠D
而∠BAD=∠1
+∠2
∠BCD=∠3
+∠4
∴
∠BAD
=
∠BCD
平行四边形对边相等、对角相等
连接对角线BD,尝试证明
练一练
如图,在 ABCD中,点M,N分别是边AB,CD的中点.
求证:AN=CM.
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠D=∠B
∵M,N分别是AB、CD的中点,
∴DN=
CD,BM=
AB,
∴DN=BM,
∴
ADN≌ CBM
,
∴AN=CM.
探索与思考
A
B
D
C
已知 ABCD,求证:∠A与∠B,∠A与∠D之间的关系.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∠A+∠D=180°
平行四边形相邻的两个角互补
你能通过不画辅助线的方法证明平行四边形对角相等吗?
探索两条平行线之间的距离
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
H
A
B
C
D
G
b
a
∵
a
//
b,
AD
//
GH
//
BC
∴
AGHD,
ABCD,
HGBC
∴
AD
=
GH
=
BC
两条平行线之间的平行线段相等
探索两条平行线之间的距离
A
B
C
D
a
b
H
G
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
∵
DA、GH、CB垂直于
a
∴
DA
//
GH
//
CB
而a
//
b
∴
AGHD,
ABCD,
HGBC
∴
AD
=
GH
=
BC
如果两条直线平行,那么一条直线上的所有点到另一条直线的距离都相等,
即两条直线之间的距离相等。
练一练
1.如图所示中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若,,求的度数.
【详解】
(1)在平行四边形ABCD中,
BC,,
∵AE=CF,
∴
BF,
∴四边形BEDF是平行四边形
∴
(2)∵
∴∠FAD=∠AFD=70°
而AD∥BC
∴∠FAD
=∠AFB=70°
练一练
2.已知:如图,在 ABCD中,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.求证:
(1)△ABE≌△CDF;
(2)BE∥DF.
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∵∠BAC+∠BAE=∠DCA+∠DCF=180°,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF;
(2)∵△ABE≌△CDF,
∴∠E=∠F,
∴BE∥DF.
练一练
3.如图,在中,为的中点,连结并延长交的延长线于点,求证:.
【详解】
证明:四边形是平行四边形
,
,
是的中点,
,
在和中
,
,.
练一练
4.如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.
(1)用含字母a,b的代数式表示矩形中空白部分的面积;
(2)当a=3,b=2时,求矩形中空白部分的面积.
【思路】
(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;
(2)将a=3,b=2代入(1)中即可;
【详解】
(1)S=ab﹣a﹣b+1;
(2)当a=3,b=2时,S=6﹣3﹣2+1=2;
课堂互动
Classroom
Interaction
理解平行四边形的概念
01
课后回顾
理解平行四边形的性质
02
利用平行四边形的性质
解决实际问题
03
THANKS
“
”
