沪教版七年级数学下册14.2全等三角形(基础知识点+题型巩固40题含答案)
文档属性
| 名称 | 沪教版七年级数学下册14.2全等三角形(基础知识点+题型巩固40题含答案) | 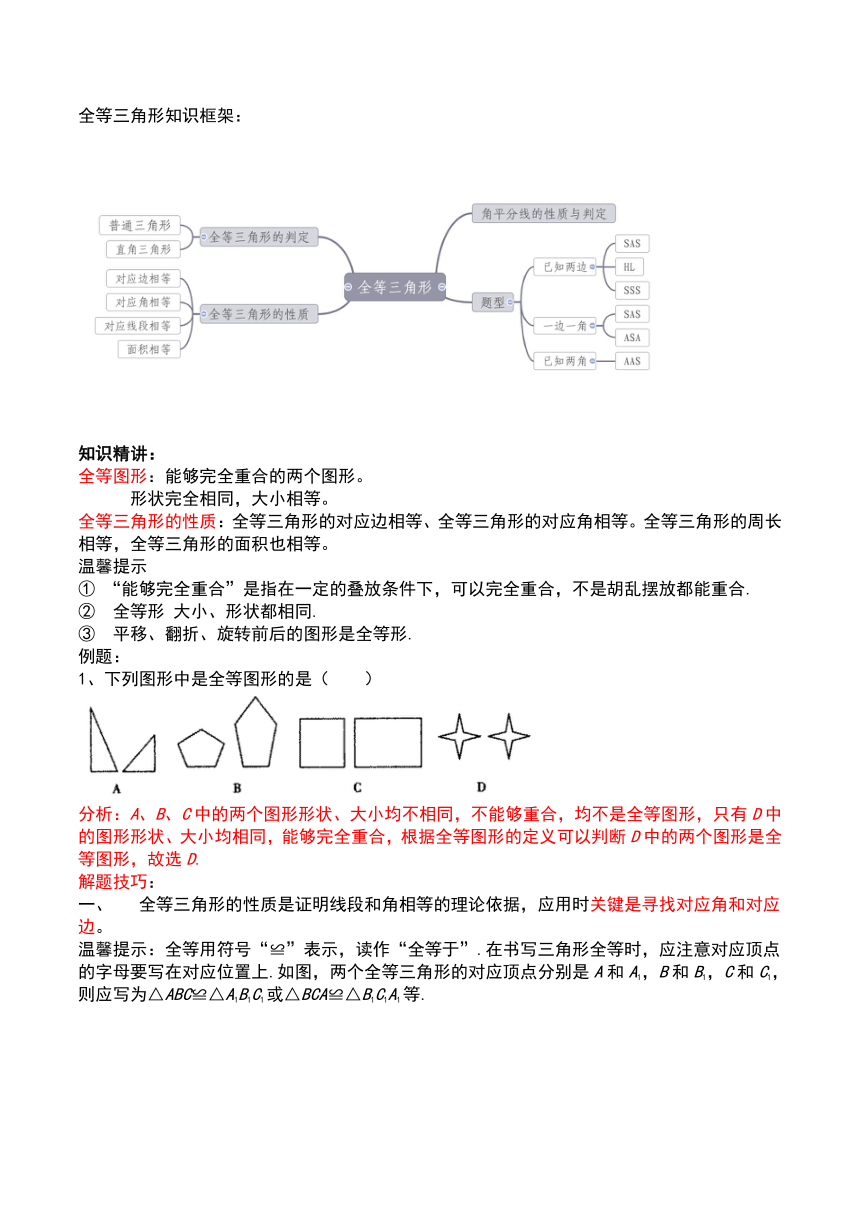 | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 09:58:32 | ||
图片预览




文档简介
全等三角形知识框架:
知识精讲:
全等图形:能够完全重合的两个图形。
形状完全相同,大小相等。
全等三角形的性质:全等三角形的对应边相等、全等三角形的对应角相等。全等三角形的周长相等,全等三角形的面积也相等。
温馨提示
① “能够完全重合”是指在一定的叠放条件下,可以完全重合,不是胡乱摆放都能重合.
② 全等形 大小、形状都相同.
③ 平移、翻折、旋转前后的图形是全等形.
例题:
1、下列图形中是全等图形的是( )
分析:A、B、C中的两个图形形状、大小均不相同,不能够重合,均不是全等图形,只有D中的图形形状、大小均相同,能够完全重合,根据全等图形的定义可以判断D中的两个图形是全等图形,故选D.
解题技巧:
全等三角形的性质是证明线段和角相等的理论依据,应用时关键是寻找对应角和对应边。
温馨提示:全等用符号“≌”表示,读作“全等于”.在书写三角形全等时,应注意对应顶点的字母要写在对应位置上.如图,两个全等三角形的对应顶点分别是A和A1,B和B1,C和C1,则应写为△ABC≌△A1B1C1或△BCA≌△B1C1A1等.
正确区分对应边与对边,对应角与对角的概念。一般地:对应边、对应角针对全等三角形,对边、对角是对同一个三角形的边和角而言的,对边是指角的对边,对角是指边的对角。
例如:如图,△ABC和△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角。
表示两个角全等时,表示对应顶点的字母要写在对应的位置上;也就是题中出现两个三角形全等我们就可以利用对应的字母寻找对应角以及对应边。“有三个角对应相等”或“有两边及其中一边的对应角对应相等”的两个三角形不一定全等;
时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。
全等交换:
全等变换是指只改变图形的位置,而不改变图形的形状和大小的变换.
如图①,把△ABC沿直线BC移动线段BC的距离,可以变到△ECD的位置;如图②,以直线BC为轴把△ABC翻折,可以变到△DBC的位置;如图③,以点A以点为中心把△ABC旋转180°,可以变到△AED的位置.像这样,只改变图形的位置,而不改变其形状、大小的图形变换叫做全等变换.在全等变换中可以清楚地识别全等三角形的对应元素.以上三种全等变换分别叫做平移变换、翻折变换和旋转变化.
温馨提示
图形是否全等,有的很容易看出来,而有的则需要通过平移、翻折或旋转后,才能发现它们的形状相同、大小相等,从而判定全等.(2)有的图形不只进行一次变换,多种变换以后的图形依然是全等的.
例题:
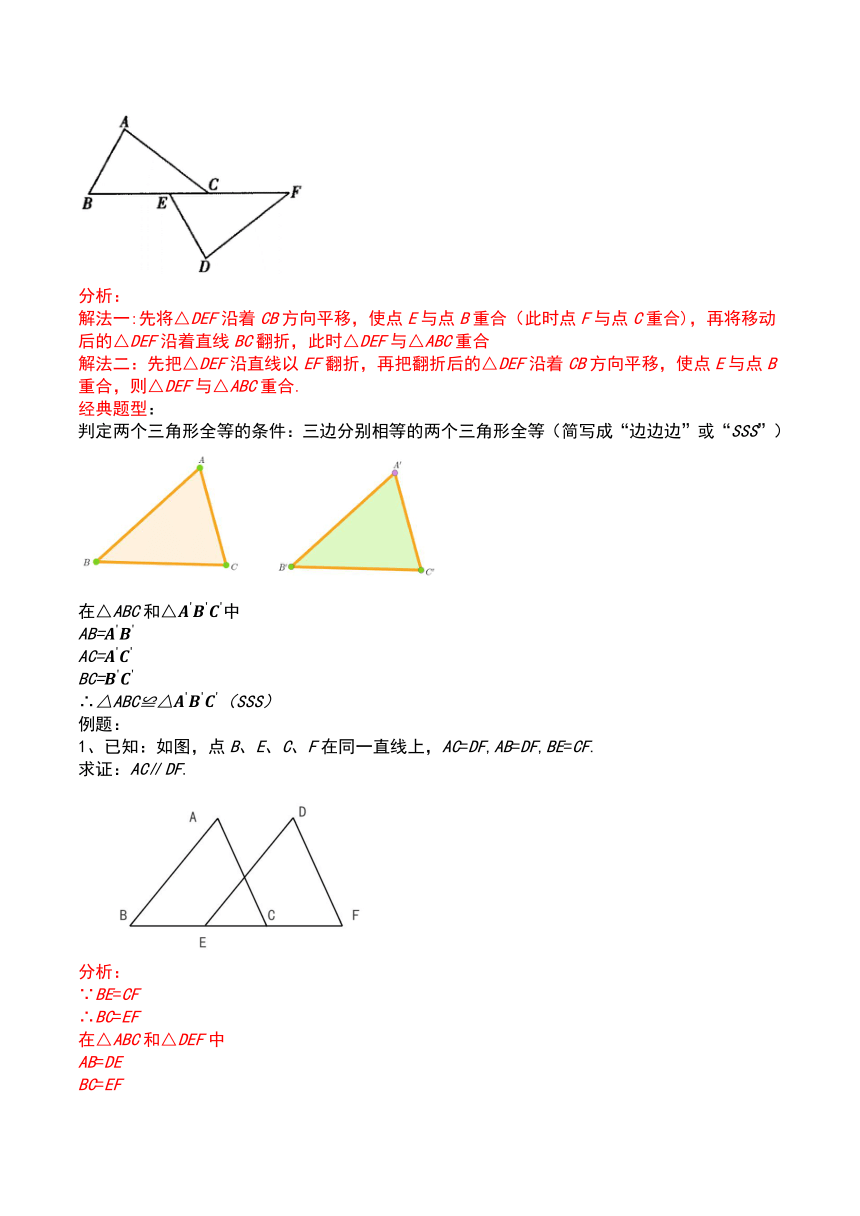
如图,△ ABC和△DEF全等,问经过怎样的图形变换,可使这两个三角形重合?
分析:
解法一:先将△DEF沿着CB方向平移,使点E与点B重合(此时点F与点C重合),再将移动后的△DEF沿着直线BC翻折,此时△DEF与△ABC重合
解法二:先把△DEF沿直线以EF翻折,再把翻折后的△DEF沿着CB方向平移,使点E与点B重合,则△DEF与△ABC重合.
经典题型:
判定两个三角形全等的条件:三边分别相等的两个三角形全等(简写成“边边边”或“SSS”)
在△ABC和△中
AB=
AC=
BC=
∴△ABC≌△(SSS)
例题:
1、已知:如图,点B、E、C、F在同一直线上,AC=DF,AB=DF,BE=CF.
求证:AC∥DF.
分析:
∵BE=CF
∴BC=EF
在△ABC和△DEF中
AB=DE
BC=EF
AC=DF
∴△ABC≌△DEF(SSS)
∴∠ACB=∠F
∴AC∥DF.
2、已知,如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF.
分析:
∵AF=DC
∴AF-CF=DC-CF,即AC=DF
在△ABC和△DEF中
AC=DF
AB=DE
BC=EF
∴△ABC≌△DEF(SSS)
3、如图,AB=CD,AE=DF,CE=FB,求证:∠BAE=∠CDF.
分析:
∵CE=BF,∴CE+EF=BF+EF,即CF=BE.
在△ABE和△DCF中
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF(SSS).
∴∠BAE=∠CDF(全等三角形的对应角相等).
判定两个三角形全等的条件:
两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)运用“SAS”证明三角形全等时,一定要找准对应相等的边、角,要注意隐含的等角,如等角、公共角、对顶角、角平分线等;在书写“SAS”的格式时,要按照“SAS”的顺序书写,以表明三个元素的位置关系;“SSA”不能证明两个三角形全等.
在△ABC和△中
AB=
∠A=∠
AC=
∴△ABC≌△(SAS)
例题:
如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD
分析:在△ADB和△BAC中
AD=BC
∠DAB=∠CBA
AB=BA
∴△ADB≌△BCA(SAS)
∴BD=AC
如图,点A、B、C、D在同一直线上,CE∥DF,AC=DF,CE=BD,求证:∠A=∠F.
分析:
∵CE∥DF
∴∠ACE=∠D
在△ACE和△FDB中
AC=FD
∠ACE=∠D
CE=DB
∴△ACE≌△FDB(SAS)
∴∠A=∠F.
如图,AB=AD,AC平分∠BAD,求证:△ABC≌△ADC.
分析:∵AC平分∠BAD,∴∠BAC=∠DAC.
在△ABC和△ADC中
AB=AD
∠BAC=∠DAC
AC=AC
∴△ABC≌△ADC(SAS).
判定两个三角形全等的条件:
两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
在△ABC和△中
∠B=∠
BC=
∠C=∠
∴△ABC≌△(ASA)
例题:
已知,∠C=∠CAF=90°,点E在AC上,且AE=BC,EF⊥AB于点D.求证AB=FE
分析:
∵EF⊥AB于点D,
∴∠ADE=90°
∴∠1+∠2=90°
又∵∠C=90°
∴∠1+∠B=90°
∴∠B=∠2
在△ABC和△FEA和
∠B=∠2
BC=AE
∠C=∠FAE
∴△ABC≌△FEA(ASA)
∴AB=FE
如图,已知EC =AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.
分析:由已知条件求得∠BCA=∠DCE,再利用“ASA”
判定△BCA≌△DCE,即可得证.
证明∵∠BCE=∠DCA,
∴∠BCE+∠ACE= ∠DCA+∠ACE,
即∠BCA=∠DCE.又∵AC=EC,∠A=∠E,
∴△BCA≌△DCE(ASA).∴BC =DC.
判定两个三角形全等的条件:
两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)“AAS”是由“ASA”推导得出的,将两者结合起来可知:两个三角形如果其备两个角和一条边对应相等,就可判定其全等.
在△ABC和△中
∠B=∠
∠C=∠
AB=
∴△ABC≌△(AAS)
例题:
1、如图,已知∠1=∠2,∠C=∠D,求证:OC=OD.
分析:
在△ABC于△BAD中
∠1=∠2
∠C=∠D
AB=BA
∴△ABC≌△BAD(AAS)
∴AD=BC
∵∠1=∠2
∴AO=BO
∴AD-AO=BC-BO
即OC=OD.
2、已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.
分析:
∵BF∥AC
∴∠F=∠FCA
∵Rt△ACD中,CE⊥AD
∴∠BCF+∠F=90°,∠BCF+∠ADC=90°
∴∠F=∠ADC
在△ACD和△CBF中
∠ACD=∠CBF=90°
∠F=∠ADC
AC=BC
∴△ACD≌△CBF(AAS)
∴CD=BF
∵D为BC中点
∴CD=BD
∴BF=CD=BD=BC=AC
则AC=2BF
判定两个直角三角形全等的方法:
斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边与直角边”或“HL”)
在Rt△ABC和Rt△中
AB=
BC=
∴Rt△ABC≌Rt△(HL)
例题:
1、如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为?若添加条件AC=EC.则可以用-----公理(或定理)判定全等。
分析:
∵AB⊥BD,AB∥ED
∴ED⊥BD
∴∠B=∠D=90°
第一小问:∵AB=ED
∴在△ABC和△EDC中
当BC=DC时,
△ABC≌△EDC(SAS)
第二小问:
在Rt△ABC和Rt△EDC中
AB=ED
AC=EC
∴Rt△ABC≌Rt△EDC(HL)
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE.AE⊥BE,垂足为E.求证:AD=AE.
分析:
∵AB=AC,点D是BC的中点,
∴AD⊥BC
∴∠ADB=90°
∵AE⊥AB
∴∠E=90°=∠ADB
∵AB平分∠DAE
∴∠BAD=∠BAE
在△ADB和△AEB中
∠ADB=∠E
∠BAD=∠BAE
AB=AB
∴△ADB≌△AEB(AAS)
∴AD=AE
4、如图,AD是△ABC的高,E是AD上一点,
BE的延长线交AC予点F,且BE=AC,DE=AC,你能说明BE与AC垂直吗?
分析: 能.只要说明∠BFA= 90°即可,即只要说明∠l+∠2 =90°即可,又∠1+∠4=90°,∠2=∠3,所以只要说明∠3=∠4即可.应考虑△BED和△ACD全等.以下证明略
关于三角影全等的总结:
一般三角形的判定方法 1.定义法:能够完全重合的两个三角形全等
2.SAS:两条边及其夹角对应相等的两个三角形全等
3.ASA:两个角及其夹边对应相等的两个三角形全等
4.AAS:两个角及其其中一个角的对边对应相等的两个三角形全等
5.SSS:三条边对应相等的两个三角形全等
直角三角形的判定方法 1.定义法;2.SAS;3.ASA;4.AAS;5.SSS;6HL
不能判定三角形全等的两种情况 1.SSA:有两边和其中一边对角对应相等的两个三角形不一定全等
2.AAA:有三个角对应相等的两个三角形不一定全等
温馨提示
①判定两个三角形全等的每件中,“边”是必不可少的.
②“SAS”包含“边”和“角”两种元素,是两边夹一角
而不是两边和其中一边对角对应相等,一定要注意元素的“对应”关系.
③“HL”是直角三角形所独有的,对于一般三角形不成立.
能力提升:(简单——中等练习题)
1、如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F,求证AC=EF
【解析】△CAB≌△FED(AAS)
2、已知:如图,点D是△ABC内的一点,且满足BD=CD,∠ABD=∠ACD,求证:AB=AC;AD⊥BC
【解析】(1)BD=CD,则∠DBC=∠DCB,所以∠ABC=∠ACB,则AB=AC
(2)证△ABD≌△ACD(SAS)得AD平分∠BAC
延长AD与BC相交,根据等腰三角形三线合一性质可证的AD⊥BC
如图,四边形ABCD中,AD=BC,且AD∥BC,E、F是对角线AC上两点,AE=CF.求证△ADF≌△CBE.
【解析】由AE=CF得AF=CE,索伊△ADF≌CBE(SAS)
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且∠GDF=∠ADF.
求证:△ADE≌△BFE
连接EG,判断EG与DF的位置关系,并说明理由.
【解析】(1)△ADE≌△BFE(ASA)或(AAS)
(2)由(1)可知E是FD的中点,因为∠GDF=∠ADF=∠F,∴GD=GF
∴根据等腰三角形三线合一的性质,GE垂直且平分DF
已知,如图△ABC中,AB=AC,∠A=50°,BD=CE,BF=CD,求∠FDE的度数。
【解析】∠A=50°,AB=AC得出∠B=∠C=65°
可证△FBD≌DCE(SAS)得∠BFD=∠CDE得∠EDF=∠B=65°
如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B=∠D互余。
试说明:∠A=∠D.
若AE=1,AC=CD=2.5,求BD的长.
【解析】(1)∠B+∠D=90°得DF⊥AB,根据8字型(∠A+∠AFD=∠D+∠ACD)可证∠A=∠D
根据ASA可证△ABC≌△DEC,得BD=BC+CD=1.5+2.5=4
如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB,△BEC的周长为22,BC=9.
求∠EBC的度数.
求三角形ABC的周长.
【解析】(1)∵AB=AC∴∠ABC=(180°-36°)÷2=72°
又ED垂直平分AB∴∠A=∠ABE∴∠EBC=72°-36°=36°
(2)根据垂直平分线的性质得AE=BE
∴AC+BC=22根据BC=9可得AC=13
∴C△ABC=35
如图在△ABC与△ABD中,BC=BD,点E为BC中点,点F为BD中点,连接AE,AF,AE=AF.求证∠C=∠D.
【解析】先证△ABE≌ABF(SSS),再证△ABC≌ABD(SAS)即可
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过点C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连结DF.
求证:BD=CF
若CE=4,求△BDF的面积.
【解析】(1)证△BAD≌△CAF(ASA)即可
(2)根据BD是角平分线,CE⊥BD可证BF=BC且E是CF的中点
所以S△BDF=·BD·EF=×8×4=16
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.
求证:△ACD≌△BEC;CF⊥DE.
【解析】(1)SAS可证三角形全等
等腰三角形的性质,底边上三线合一可证CF⊥DE
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
若∠CAE=30°,求∠ACF的度数.
求证:AB=CE+BF.
【解析】(1)△FBC≌△EBA(HL)得∠EAB=∠FCB=15°,所以∠ACF=60°
由(1)可知BF=BE,∴AB=BC=CE+BE=CE+BF
已知△ABC,其中AB=BC=AC,∠BAC=∠B=∠ACB=60°,点D、E分别在AB,BC上且AD=BE,线段AE,CD相交于点F.
AE与CD相等吗?请说明理由.
求∠AFC的度数.
【解析】(1)△ABE≌△CAD(SAS)得AE=CD
(2)∠AFC=∠EAD+∠ADC=∠EAD+∠AEB=120°
14、如图,△ABC是等边三角形,点E、F分别在边AB和AC上,且AE=BF.
(1)求证:△ABE≌△BCF
(2)若∠ABE=20°,求∠ACF的度数
(3)猜测∠BOC的度数并证明你的猜想
【解析】(1)△ABE≌△BCF(SAS)
(2)∠ACF=∠ACB-∠FCB=40°
(3)∠BOC=120°;∵∠BOF=∠A=60°(A字型:即∠BOF+∠BFO=∠A+∠AEB)
15、如图,在△ABC中,∠ACB=90°,AC=BC,AE是边BC的中线,过点C作CF⊥AE,垂足点为F,过点B作BD⊥BC交CF的延长线于点D.
(1)试说明:AF=CD
(2)若AC=12cm,求线段BD的长度.
【解析】
(1)证明△DBC≌△ECA(AAS或ASA)
(2)由(1)可知BD=EC= AC
16、如图:在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变,求证:△AEF≌△BCF.
【解析】等腰三角形三线合一的性质
等腰三角形底边中线,垂线,顶角角平分线三线合一。
(1)AD是BC的垂直平分线,∴BE=CE
(2)∠CAD=22.5°,∠FBC=22.5,AF=BF,所以△AEF≌△BCF(ASA)
17、如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
(1)求证:DB=BC.
(2)若BD=6cm,求AC的长.
【解析】(1)证△DBE≌△BCA(AAS/ASA)
AC=3cm
18、在△ABC中,BC=AC,∠BCA=90°,P为直线上AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,请说明:BO=AQ.
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?
【解析】(1)证△CBP≌△CAQ(AAS)
(2)成立
19、如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF
(2)在AB上取点M,使BM=2DE,连接MC,连接MC,交AD于点N,连接ME,求证:ME⊥BC;CM平分∠ACB;DE=DN.
【解析】
△AFC≌△AEB(ASA)
20、如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE于点G,与EF交于点H.
(1)证明:AD垂直平分CE
(2)若∠BCE=40°,求∠EHD的度数.
【解析】
(1)证△AEG≌△ACG(SAS)即可
(2)50°
21、如图,∠ABC=90°,D,E分别在BC、AC上,AD⊥DE,且AD=DE,连结MC.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?请说明理由.
【解析】添加条件:“F是AE中点”
(1)△ADM≌△DEC(AAS),∵FD=DE;∴FM=FC
(2)AD⊥MC,∵ED∥MC,AD⊥DE;∴AD⊥MC
22、图中是一副三角板, 45°的三角板 Rt △DEF的直角顶点 D 恰好在 30° 的三角板 Rt △ABC斜边 AB 的中点处,∠A=30°,∠E= 45°,∠EDF=∠ACB= 90°, DE 交 AC 于点G ,GM ⊥AB于点M .
(1)如图 1,当DF 经过点C 时,作CN⊥ AB于点N ,求证: AM= DN ? .
(2)如图 2,当 DF ∥AC时,DF 交 BC 于H ,作 HN ⊥AB于N ,(1)的结论仍 然成立,请你说明理由.
分析:】⑴ ∵∠A= 30° ,∠ACB=90°,D是AB 的重点,∴BC=BD,∠B=60°
∴△BCD是等边三角形
又∵CN⊥DB,∴DN=DB,
∵∠EDF=90°,△BCD是等边三角形
∴∠ADG=30°,而∠A=30,∴GA=GD
∵GM⊥AB,∴AM=AD
又∵AD=DB,∴AM=DN
(2)∵DF∥AC,∴∠BDF=∠A=30°,∠AGD=∠GDH=90°,
∴∠ADG=60°
∵∠B=60°,AD=DB
∴△ADG≌△DBH,∴AG=DH
又∵∠BDF=∠A
GM⊥AB,HN⊥AB
∴△AMG≌△DNH,∴AM=DN.
23、已知:BD CE是△ABC的高,点 P 在 BD的延长线上,BP =AC ,点Q 在CE 上,CQ =AB =,求证:⑴ AP =AQ =;⑵ AP⊥AQ ?
【解析】如图,设CE 交 BD于F. ⑴ 由BD垂直 CA,CE⊥AB ,知∠BEF= CDF=90°而 ∠BFE=∠CFD,故∠ABD=QCA. 由已知,有AB =QC ,BP= CA ,从而△ABP≌△QCA ? ?即有AP=AQ .⑵ 由⑴可得∠AQC=∠PAB,而∠AQC =∠QEA+∠QAE=∠QAE+90° ? ?∠PAB=∠PAQ+∠QAE从而可得∠PAQ =90°,即AP⊥AQ .
知识精讲:
全等图形:能够完全重合的两个图形。
形状完全相同,大小相等。
全等三角形的性质:全等三角形的对应边相等、全等三角形的对应角相等。全等三角形的周长相等,全等三角形的面积也相等。
温馨提示
① “能够完全重合”是指在一定的叠放条件下,可以完全重合,不是胡乱摆放都能重合.
② 全等形 大小、形状都相同.
③ 平移、翻折、旋转前后的图形是全等形.
例题:
1、下列图形中是全等图形的是( )
分析:A、B、C中的两个图形形状、大小均不相同,不能够重合,均不是全等图形,只有D中的图形形状、大小均相同,能够完全重合,根据全等图形的定义可以判断D中的两个图形是全等图形,故选D.
解题技巧:
全等三角形的性质是证明线段和角相等的理论依据,应用时关键是寻找对应角和对应边。
温馨提示:全等用符号“≌”表示,读作“全等于”.在书写三角形全等时,应注意对应顶点的字母要写在对应位置上.如图,两个全等三角形的对应顶点分别是A和A1,B和B1,C和C1,则应写为△ABC≌△A1B1C1或△BCA≌△B1C1A1等.
正确区分对应边与对边,对应角与对角的概念。一般地:对应边、对应角针对全等三角形,对边、对角是对同一个三角形的边和角而言的,对边是指角的对边,对角是指边的对角。
例如:如图,△ABC和△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角。
表示两个角全等时,表示对应顶点的字母要写在对应的位置上;也就是题中出现两个三角形全等我们就可以利用对应的字母寻找对应角以及对应边。“有三个角对应相等”或“有两边及其中一边的对应角对应相等”的两个三角形不一定全等;
时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。
全等交换:
全等变换是指只改变图形的位置,而不改变图形的形状和大小的变换.
如图①,把△ABC沿直线BC移动线段BC的距离,可以变到△ECD的位置;如图②,以直线BC为轴把△ABC翻折,可以变到△DBC的位置;如图③,以点A以点为中心把△ABC旋转180°,可以变到△AED的位置.像这样,只改变图形的位置,而不改变其形状、大小的图形变换叫做全等变换.在全等变换中可以清楚地识别全等三角形的对应元素.以上三种全等变换分别叫做平移变换、翻折变换和旋转变化.
温馨提示
图形是否全等,有的很容易看出来,而有的则需要通过平移、翻折或旋转后,才能发现它们的形状相同、大小相等,从而判定全等.(2)有的图形不只进行一次变换,多种变换以后的图形依然是全等的.
例题:
如图,△ ABC和△DEF全等,问经过怎样的图形变换,可使这两个三角形重合?
分析:
解法一:先将△DEF沿着CB方向平移,使点E与点B重合(此时点F与点C重合),再将移动后的△DEF沿着直线BC翻折,此时△DEF与△ABC重合
解法二:先把△DEF沿直线以EF翻折,再把翻折后的△DEF沿着CB方向平移,使点E与点B重合,则△DEF与△ABC重合.
经典题型:
判定两个三角形全等的条件:三边分别相等的两个三角形全等(简写成“边边边”或“SSS”)
在△ABC和△中
AB=
AC=
BC=
∴△ABC≌△(SSS)
例题:
1、已知:如图,点B、E、C、F在同一直线上,AC=DF,AB=DF,BE=CF.
求证:AC∥DF.
分析:
∵BE=CF
∴BC=EF
在△ABC和△DEF中
AB=DE
BC=EF
AC=DF
∴△ABC≌△DEF(SSS)
∴∠ACB=∠F
∴AC∥DF.
2、已知,如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF.
分析:
∵AF=DC
∴AF-CF=DC-CF,即AC=DF
在△ABC和△DEF中
AC=DF
AB=DE
BC=EF
∴△ABC≌△DEF(SSS)
3、如图,AB=CD,AE=DF,CE=FB,求证:∠BAE=∠CDF.
分析:
∵CE=BF,∴CE+EF=BF+EF,即CF=BE.
在△ABE和△DCF中
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF(SSS).
∴∠BAE=∠CDF(全等三角形的对应角相等).
判定两个三角形全等的条件:
两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)运用“SAS”证明三角形全等时,一定要找准对应相等的边、角,要注意隐含的等角,如等角、公共角、对顶角、角平分线等;在书写“SAS”的格式时,要按照“SAS”的顺序书写,以表明三个元素的位置关系;“SSA”不能证明两个三角形全等.
在△ABC和△中
AB=
∠A=∠
AC=
∴△ABC≌△(SAS)
例题:
如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD
分析:在△ADB和△BAC中
AD=BC
∠DAB=∠CBA
AB=BA
∴△ADB≌△BCA(SAS)
∴BD=AC
如图,点A、B、C、D在同一直线上,CE∥DF,AC=DF,CE=BD,求证:∠A=∠F.
分析:
∵CE∥DF
∴∠ACE=∠D
在△ACE和△FDB中
AC=FD
∠ACE=∠D
CE=DB
∴△ACE≌△FDB(SAS)
∴∠A=∠F.
如图,AB=AD,AC平分∠BAD,求证:△ABC≌△ADC.
分析:∵AC平分∠BAD,∴∠BAC=∠DAC.
在△ABC和△ADC中
AB=AD
∠BAC=∠DAC
AC=AC
∴△ABC≌△ADC(SAS).
判定两个三角形全等的条件:
两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
在△ABC和△中
∠B=∠
BC=
∠C=∠
∴△ABC≌△(ASA)
例题:
已知,∠C=∠CAF=90°,点E在AC上,且AE=BC,EF⊥AB于点D.求证AB=FE
分析:
∵EF⊥AB于点D,
∴∠ADE=90°
∴∠1+∠2=90°
又∵∠C=90°
∴∠1+∠B=90°
∴∠B=∠2
在△ABC和△FEA和
∠B=∠2
BC=AE
∠C=∠FAE
∴△ABC≌△FEA(ASA)
∴AB=FE
如图,已知EC =AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.
分析:由已知条件求得∠BCA=∠DCE,再利用“ASA”
判定△BCA≌△DCE,即可得证.
证明∵∠BCE=∠DCA,
∴∠BCE+∠ACE= ∠DCA+∠ACE,
即∠BCA=∠DCE.又∵AC=EC,∠A=∠E,
∴△BCA≌△DCE(ASA).∴BC =DC.
判定两个三角形全等的条件:
两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)“AAS”是由“ASA”推导得出的,将两者结合起来可知:两个三角形如果其备两个角和一条边对应相等,就可判定其全等.
在△ABC和△中
∠B=∠
∠C=∠
AB=
∴△ABC≌△(AAS)
例题:
1、如图,已知∠1=∠2,∠C=∠D,求证:OC=OD.
分析:
在△ABC于△BAD中
∠1=∠2
∠C=∠D
AB=BA
∴△ABC≌△BAD(AAS)
∴AD=BC
∵∠1=∠2
∴AO=BO
∴AD-AO=BC-BO
即OC=OD.
2、已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.
分析:
∵BF∥AC
∴∠F=∠FCA
∵Rt△ACD中,CE⊥AD
∴∠BCF+∠F=90°,∠BCF+∠ADC=90°
∴∠F=∠ADC
在△ACD和△CBF中
∠ACD=∠CBF=90°
∠F=∠ADC
AC=BC
∴△ACD≌△CBF(AAS)
∴CD=BF
∵D为BC中点
∴CD=BD
∴BF=CD=BD=BC=AC
则AC=2BF
判定两个直角三角形全等的方法:
斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边与直角边”或“HL”)
在Rt△ABC和Rt△中
AB=
BC=
∴Rt△ABC≌Rt△(HL)
例题:
1、如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为?若添加条件AC=EC.则可以用-----公理(或定理)判定全等。
分析:
∵AB⊥BD,AB∥ED
∴ED⊥BD
∴∠B=∠D=90°
第一小问:∵AB=ED
∴在△ABC和△EDC中
当BC=DC时,
△ABC≌△EDC(SAS)
第二小问:
在Rt△ABC和Rt△EDC中
AB=ED
AC=EC
∴Rt△ABC≌Rt△EDC(HL)
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE.AE⊥BE,垂足为E.求证:AD=AE.
分析:
∵AB=AC,点D是BC的中点,
∴AD⊥BC
∴∠ADB=90°
∵AE⊥AB
∴∠E=90°=∠ADB
∵AB平分∠DAE
∴∠BAD=∠BAE
在△ADB和△AEB中
∠ADB=∠E
∠BAD=∠BAE
AB=AB
∴△ADB≌△AEB(AAS)
∴AD=AE
4、如图,AD是△ABC的高,E是AD上一点,
BE的延长线交AC予点F,且BE=AC,DE=AC,你能说明BE与AC垂直吗?
分析: 能.只要说明∠BFA= 90°即可,即只要说明∠l+∠2 =90°即可,又∠1+∠4=90°,∠2=∠3,所以只要说明∠3=∠4即可.应考虑△BED和△ACD全等.以下证明略
关于三角影全等的总结:
一般三角形的判定方法 1.定义法:能够完全重合的两个三角形全等
2.SAS:两条边及其夹角对应相等的两个三角形全等
3.ASA:两个角及其夹边对应相等的两个三角形全等
4.AAS:两个角及其其中一个角的对边对应相等的两个三角形全等
5.SSS:三条边对应相等的两个三角形全等
直角三角形的判定方法 1.定义法;2.SAS;3.ASA;4.AAS;5.SSS;6HL
不能判定三角形全等的两种情况 1.SSA:有两边和其中一边对角对应相等的两个三角形不一定全等
2.AAA:有三个角对应相等的两个三角形不一定全等
温馨提示
①判定两个三角形全等的每件中,“边”是必不可少的.
②“SAS”包含“边”和“角”两种元素,是两边夹一角
而不是两边和其中一边对角对应相等,一定要注意元素的“对应”关系.
③“HL”是直角三角形所独有的,对于一般三角形不成立.
能力提升:(简单——中等练习题)
1、如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F,求证AC=EF
【解析】△CAB≌△FED(AAS)
2、已知:如图,点D是△ABC内的一点,且满足BD=CD,∠ABD=∠ACD,求证:AB=AC;AD⊥BC
【解析】(1)BD=CD,则∠DBC=∠DCB,所以∠ABC=∠ACB,则AB=AC
(2)证△ABD≌△ACD(SAS)得AD平分∠BAC
延长AD与BC相交,根据等腰三角形三线合一性质可证的AD⊥BC
如图,四边形ABCD中,AD=BC,且AD∥BC,E、F是对角线AC上两点,AE=CF.求证△ADF≌△CBE.
【解析】由AE=CF得AF=CE,索伊△ADF≌CBE(SAS)
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且∠GDF=∠ADF.
求证:△ADE≌△BFE
连接EG,判断EG与DF的位置关系,并说明理由.
【解析】(1)△ADE≌△BFE(ASA)或(AAS)
(2)由(1)可知E是FD的中点,因为∠GDF=∠ADF=∠F,∴GD=GF
∴根据等腰三角形三线合一的性质,GE垂直且平分DF
已知,如图△ABC中,AB=AC,∠A=50°,BD=CE,BF=CD,求∠FDE的度数。
【解析】∠A=50°,AB=AC得出∠B=∠C=65°
可证△FBD≌DCE(SAS)得∠BFD=∠CDE得∠EDF=∠B=65°
如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B=∠D互余。
试说明:∠A=∠D.
若AE=1,AC=CD=2.5,求BD的长.
【解析】(1)∠B+∠D=90°得DF⊥AB,根据8字型(∠A+∠AFD=∠D+∠ACD)可证∠A=∠D
根据ASA可证△ABC≌△DEC,得BD=BC+CD=1.5+2.5=4
如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB,△BEC的周长为22,BC=9.
求∠EBC的度数.
求三角形ABC的周长.
【解析】(1)∵AB=AC∴∠ABC=(180°-36°)÷2=72°
又ED垂直平分AB∴∠A=∠ABE∴∠EBC=72°-36°=36°
(2)根据垂直平分线的性质得AE=BE
∴AC+BC=22根据BC=9可得AC=13
∴C△ABC=35
如图在△ABC与△ABD中,BC=BD,点E为BC中点,点F为BD中点,连接AE,AF,AE=AF.求证∠C=∠D.
【解析】先证△ABE≌ABF(SSS),再证△ABC≌ABD(SAS)即可
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过点C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连结DF.
求证:BD=CF
若CE=4,求△BDF的面积.
【解析】(1)证△BAD≌△CAF(ASA)即可
(2)根据BD是角平分线,CE⊥BD可证BF=BC且E是CF的中点
所以S△BDF=·BD·EF=×8×4=16
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.
求证:△ACD≌△BEC;CF⊥DE.
【解析】(1)SAS可证三角形全等
等腰三角形的性质,底边上三线合一可证CF⊥DE
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
若∠CAE=30°,求∠ACF的度数.
求证:AB=CE+BF.
【解析】(1)△FBC≌△EBA(HL)得∠EAB=∠FCB=15°,所以∠ACF=60°
由(1)可知BF=BE,∴AB=BC=CE+BE=CE+BF
已知△ABC,其中AB=BC=AC,∠BAC=∠B=∠ACB=60°,点D、E分别在AB,BC上且AD=BE,线段AE,CD相交于点F.
AE与CD相等吗?请说明理由.
求∠AFC的度数.
【解析】(1)△ABE≌△CAD(SAS)得AE=CD
(2)∠AFC=∠EAD+∠ADC=∠EAD+∠AEB=120°
14、如图,△ABC是等边三角形,点E、F分别在边AB和AC上,且AE=BF.
(1)求证:△ABE≌△BCF
(2)若∠ABE=20°,求∠ACF的度数
(3)猜测∠BOC的度数并证明你的猜想
【解析】(1)△ABE≌△BCF(SAS)
(2)∠ACF=∠ACB-∠FCB=40°
(3)∠BOC=120°;∵∠BOF=∠A=60°(A字型:即∠BOF+∠BFO=∠A+∠AEB)
15、如图,在△ABC中,∠ACB=90°,AC=BC,AE是边BC的中线,过点C作CF⊥AE,垂足点为F,过点B作BD⊥BC交CF的延长线于点D.
(1)试说明:AF=CD
(2)若AC=12cm,求线段BD的长度.
【解析】
(1)证明△DBC≌△ECA(AAS或ASA)
(2)由(1)可知BD=EC= AC
16、如图:在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变,求证:△AEF≌△BCF.
【解析】等腰三角形三线合一的性质
等腰三角形底边中线,垂线,顶角角平分线三线合一。
(1)AD是BC的垂直平分线,∴BE=CE
(2)∠CAD=22.5°,∠FBC=22.5,AF=BF,所以△AEF≌△BCF(ASA)
17、如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
(1)求证:DB=BC.
(2)若BD=6cm,求AC的长.
【解析】(1)证△DBE≌△BCA(AAS/ASA)
AC=3cm
18、在△ABC中,BC=AC,∠BCA=90°,P为直线上AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,请说明:BO=AQ.
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?
【解析】(1)证△CBP≌△CAQ(AAS)
(2)成立
19、如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF
(2)在AB上取点M,使BM=2DE,连接MC,连接MC,交AD于点N,连接ME,求证:ME⊥BC;CM平分∠ACB;DE=DN.
【解析】
△AFC≌△AEB(ASA)
20、如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE于点G,与EF交于点H.
(1)证明:AD垂直平分CE
(2)若∠BCE=40°,求∠EHD的度数.
【解析】
(1)证△AEG≌△ACG(SAS)即可
(2)50°
21、如图,∠ABC=90°,D,E分别在BC、AC上,AD⊥DE,且AD=DE,连结MC.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?请说明理由.
【解析】添加条件:“F是AE中点”
(1)△ADM≌△DEC(AAS),∵FD=DE;∴FM=FC
(2)AD⊥MC,∵ED∥MC,AD⊥DE;∴AD⊥MC
22、图中是一副三角板, 45°的三角板 Rt △DEF的直角顶点 D 恰好在 30° 的三角板 Rt △ABC斜边 AB 的中点处,∠A=30°,∠E= 45°,∠EDF=∠ACB= 90°, DE 交 AC 于点G ,GM ⊥AB于点M .
(1)如图 1,当DF 经过点C 时,作CN⊥ AB于点N ,求证: AM= DN ? .
(2)如图 2,当 DF ∥AC时,DF 交 BC 于H ,作 HN ⊥AB于N ,(1)的结论仍 然成立,请你说明理由.
分析:】⑴ ∵∠A= 30° ,∠ACB=90°,D是AB 的重点,∴BC=BD,∠B=60°
∴△BCD是等边三角形
又∵CN⊥DB,∴DN=DB,
∵∠EDF=90°,△BCD是等边三角形
∴∠ADG=30°,而∠A=30,∴GA=GD
∵GM⊥AB,∴AM=AD
又∵AD=DB,∴AM=DN
(2)∵DF∥AC,∴∠BDF=∠A=30°,∠AGD=∠GDH=90°,
∴∠ADG=60°
∵∠B=60°,AD=DB
∴△ADG≌△DBH,∴AG=DH
又∵∠BDF=∠A
GM⊥AB,HN⊥AB
∴△AMG≌△DNH,∴AM=DN.
23、已知:BD CE是△ABC的高,点 P 在 BD的延长线上,BP =AC ,点Q 在CE 上,CQ =AB =,求证:⑴ AP =AQ =;⑵ AP⊥AQ ?
【解析】如图,设CE 交 BD于F. ⑴ 由BD垂直 CA,CE⊥AB ,知∠BEF= CDF=90°而 ∠BFE=∠CFD,故∠ABD=QCA. 由已知,有AB =QC ,BP= CA ,从而△ABP≌△QCA ? ?即有AP=AQ .⑵ 由⑴可得∠AQC=∠PAB,而∠AQC =∠QEA+∠QAE=∠QAE+90° ? ?∠PAB=∠PAQ+∠QAE从而可得∠PAQ =90°,即AP⊥AQ .
