北师大版七年级数学下册课件——2.3平行线的性质(1) (共26张PPT)
文档属性
| 名称 | 北师大版七年级数学下册课件——2.3平行线的性质(1) (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
初中数学七年级(下)
2.3 平行线的性质(第1课时)
通过观察、操作、推理等活动,得出平行线性质定理.
掌握平行线性质定理,并能解决简单问题.
学习目标
生活中常见的平行线
复习回顾
关于平行线的判定你还记得吗?
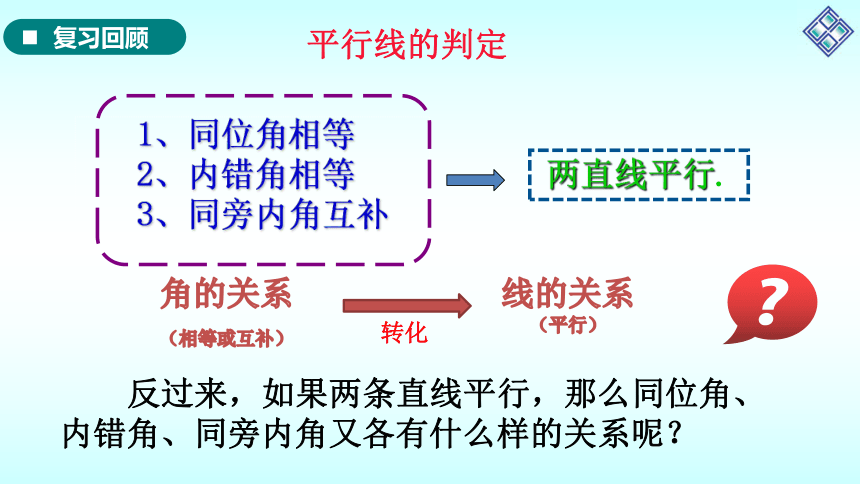
平行线的判定
复习回顾
(1)因为∠1=∠5 (已知)
所以 a∥b( )
(2)因为∠4=∠ (已知)
所以a∥b(内错角相等,两直线平行 )
(3)因为∠4+∠ =1800 (已知)
所以a∥b( )
同位角相等,两直线平行
同旁内角互补,两直线平行
5
6
平行线的判定
两直线平行.
反过来,如果两条直线平行,那么同位角、内错角、同旁内角又各有什么样的关系呢?
角的关系(相等或互补)
线的关系(平行)
1、同位角相等
2、内错角相等
3、同旁内角互补
复习回顾
转化
动手探究
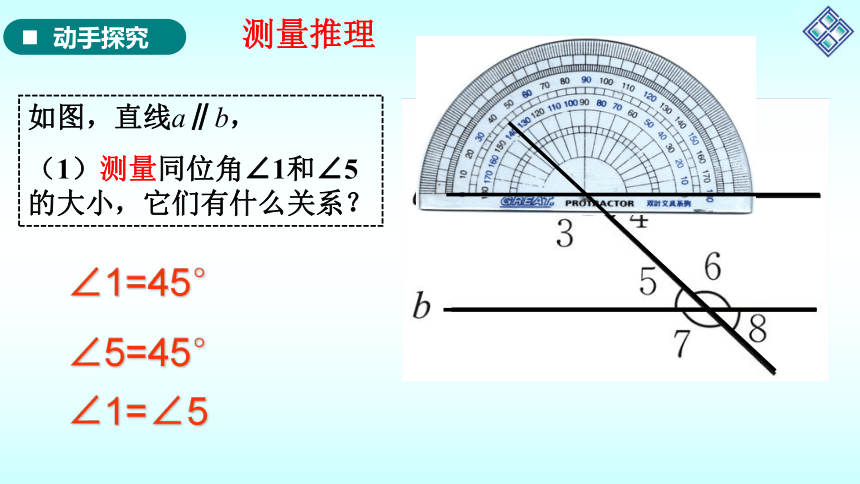
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
∠1=45°
∠1=∠5
∠5=45°
测量推理
动手探究
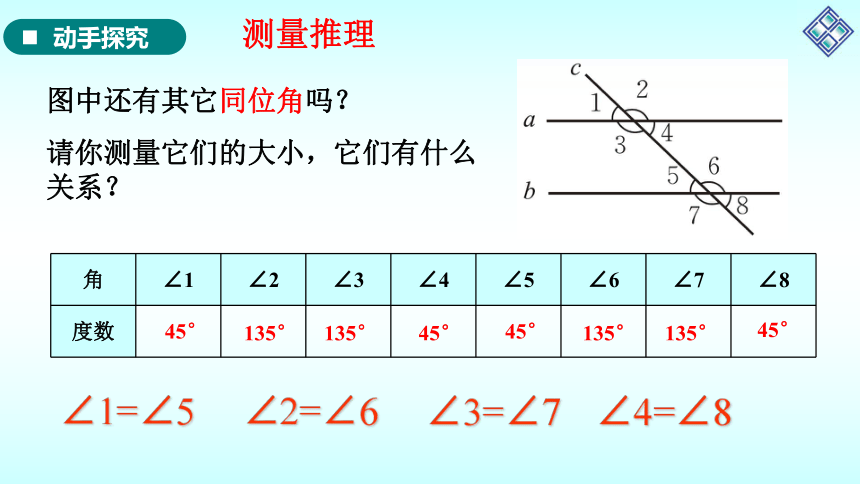
图中还有其它同位角吗?
请你测量它们的大小,它们有什么关系?
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数 45° 45°
135°
135°
135°
135°
45°
45°
测量推理
动手探究
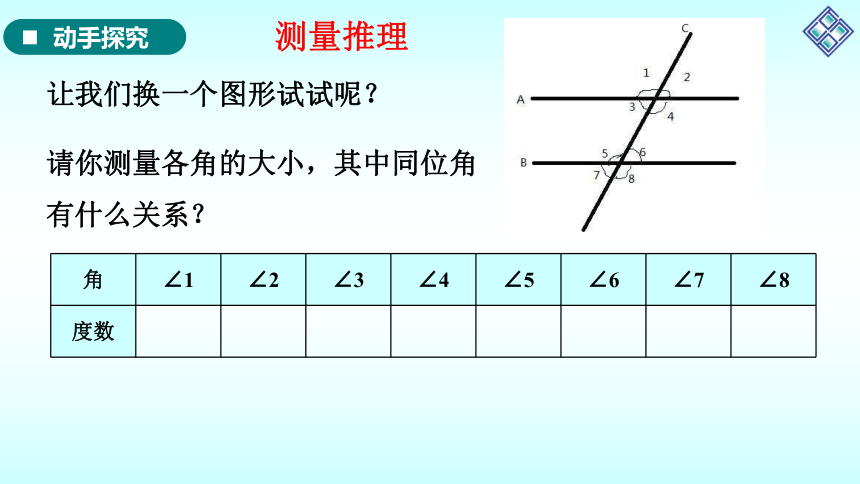
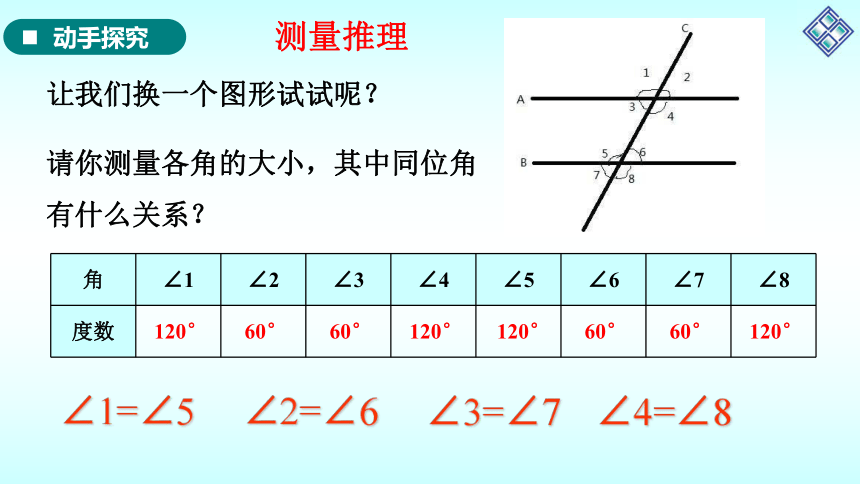
让我们换一个图形试试呢?
请你测量各角的大小,其中同位角有什么关系?
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
测量推理
动手探究
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数 120° 60° 60° 120° 120° 60° 60° 120°
测量推理
让我们换一个图形试试呢?
请你测量各角的大小,其中同位角有什么关系?
动手探究
裁剪拼接
∠1=∠5
请你将视频暂停,自己画一个类似图形,剪拼探究一下吧.(要注意安全哦)
总结结论
简称为:“两直线平行,同位角相等.”
符号表示:∵a//b
∴∠1=∠5
平行线的性质1
两条平行线被第三条直线所截,
同位角相等.
深入探究
如图,直线a∥b,
(2)图中有几对内错角?它们的大小有什么关系?为什么?
证明:∵ a∥b (已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠4(对顶角相等)
∴ ∠4=∠5(等量代换)
2对内错角
∠4=∠5=45°
∠3=∠6=135°
总结结论
简称为:“两直线平行,内错角相等.”
符号表示:∵a//b
∴∠4=∠5
平行线的性质2
两条平行线被第三条直线所截,
内错角相等.
深入探究
如图,直线a∥b,
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
2对同旁内角
∠3+∠5=180°
∠4+∠6=180°
证明:∵ a∥b (已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠3=180°(邻补角定义)
∴ ∠3+∠5=180°(等量代换)
深入探究
如图,直线a∥b,
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
2对同旁内角
∠3+∠5=180°
∠4+∠6=180°
证明:∵ a∥b (已知)
∴∠4=∠5(两直线平行,内错角相等)
又∵∠3+∠4=180°(邻补角定义)
∴ ∠3+∠5=180°(等量代换)
总结结论
简称为:“两直线平行,同旁内角互补.”
符号表示:∵a//b
∴∠3+∠5=180°
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补.
总结结论
平行线的性质总结
两直线平行.
角的关系(相等或互补)
线的关系(平行)
1、同位角相等
2、内错角相等
3、同旁内角互补
转化
实践应用
例1 如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2, ∠3=∠4 .
(1)∠1与∠3 的大小有什么关系? ∠3与∠4呢?
(2)反射光线BC与EF也平行吗?为什么?
随堂练习
(1)如果AD//BC,可得∠B=∠1,
根据_________________________
(2)如果AB//CD,
根据两直线平行,内错角相等
可得∠ =∠___
(3)如果AD//BC,根据___________________________
可得∠C+_______=180?
A
B
C
D
1
两直线平行,同位角相等
D
1
两直线平行,同旁内角互补
∠D
实践应用
例2 如图,AB//CD,∠α=45°,∠D=∠C,依次求出 ∠D,∠C,∠B 的度数.
解:∵ AB//CD
∴ ∠D=∠α=45°(两直线平行,同位角相等)
∵ ∠D=∠C
∴ ∠C=45°(等量代换)
∵ AB//CD
∴ ∠C+∠B=180°(两直线平行,同旁内角互补)
∴ ∠B=180°—∠C=135°
随堂练习
如图,已知AC//BD,AE//BF,求证∠A=∠B.请你将括号补充完整.
C
A
B
D
E
F
P
1
证明:∵AC//BD(已知)
∴∠A= ∠1 ( )
∵AE//BF(已知)
∴∠B= ∠1( )
∴∠A=∠B ( )
两直线平行,内错角相等
两直线平行,内错角相等
等量代换
问题解决
如图,从一艘船上测得一个灯塔的方向是北偏西 48°,那么这艘船在这个灯塔的什么方向?
北
东
答案:南偏东48°
1
归纳小结
(1)请你谈谈本节课的收获和感受。
(2)说说平行线的“判定”与“性质”有什么不同?
角的关系(相等或互补)
线的关系(平行)
当堂检测
请你完成《济南市初中数学2020空中课堂学习经历案》上的当堂检测。
课后作业
请你完成《济南市初中数学2020空中课堂学习经历案》上的课后练习题。
数学阅读
初中数学七年级(下)
2.3 平行线的性质(第1课时)
通过观察、操作、推理等活动,得出平行线性质定理.
掌握平行线性质定理,并能解决简单问题.
学习目标
生活中常见的平行线
复习回顾
关于平行线的判定你还记得吗?
平行线的判定
复习回顾
(1)因为∠1=∠5 (已知)
所以 a∥b( )
(2)因为∠4=∠ (已知)
所以a∥b(内错角相等,两直线平行 )
(3)因为∠4+∠ =1800 (已知)
所以a∥b( )
同位角相等,两直线平行
同旁内角互补,两直线平行
5
6
平行线的判定
两直线平行.
反过来,如果两条直线平行,那么同位角、内错角、同旁内角又各有什么样的关系呢?
角的关系(相等或互补)
线的关系(平行)
1、同位角相等
2、内错角相等
3、同旁内角互补
复习回顾
转化
动手探究
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
∠1=45°
∠1=∠5
∠5=45°
测量推理
动手探究
图中还有其它同位角吗?
请你测量它们的大小,它们有什么关系?
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数 45° 45°
135°
135°
135°
135°
45°
45°
测量推理
动手探究
让我们换一个图形试试呢?
请你测量各角的大小,其中同位角有什么关系?
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
测量推理
动手探究
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数 120° 60° 60° 120° 120° 60° 60° 120°
测量推理
让我们换一个图形试试呢?
请你测量各角的大小,其中同位角有什么关系?
动手探究
裁剪拼接
∠1=∠5
请你将视频暂停,自己画一个类似图形,剪拼探究一下吧.(要注意安全哦)
总结结论
简称为:“两直线平行,同位角相等.”
符号表示:∵a//b
∴∠1=∠5
平行线的性质1
两条平行线被第三条直线所截,
同位角相等.
深入探究
如图,直线a∥b,
(2)图中有几对内错角?它们的大小有什么关系?为什么?
证明:∵ a∥b (已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠4(对顶角相等)
∴ ∠4=∠5(等量代换)
2对内错角
∠4=∠5=45°
∠3=∠6=135°
总结结论
简称为:“两直线平行,内错角相等.”
符号表示:∵a//b
∴∠4=∠5
平行线的性质2
两条平行线被第三条直线所截,
内错角相等.
深入探究
如图,直线a∥b,
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
2对同旁内角
∠3+∠5=180°
∠4+∠6=180°
证明:∵ a∥b (已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠3=180°(邻补角定义)
∴ ∠3+∠5=180°(等量代换)
深入探究
如图,直线a∥b,
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
2对同旁内角
∠3+∠5=180°
∠4+∠6=180°
证明:∵ a∥b (已知)
∴∠4=∠5(两直线平行,内错角相等)
又∵∠3+∠4=180°(邻补角定义)
∴ ∠3+∠5=180°(等量代换)
总结结论
简称为:“两直线平行,同旁内角互补.”
符号表示:∵a//b
∴∠3+∠5=180°
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补.
总结结论
平行线的性质总结
两直线平行.
角的关系(相等或互补)
线的关系(平行)
1、同位角相等
2、内错角相等
3、同旁内角互补
转化
实践应用
例1 如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2, ∠3=∠4 .
(1)∠1与∠3 的大小有什么关系? ∠3与∠4呢?
(2)反射光线BC与EF也平行吗?为什么?
随堂练习
(1)如果AD//BC,可得∠B=∠1,
根据_________________________
(2)如果AB//CD,
根据两直线平行,内错角相等
可得∠ =∠___
(3)如果AD//BC,根据___________________________
可得∠C+_______=180?
A
B
C
D
1
两直线平行,同位角相等
D
1
两直线平行,同旁内角互补
∠D
实践应用
例2 如图,AB//CD,∠α=45°,∠D=∠C,依次求出 ∠D,∠C,∠B 的度数.
解:∵ AB//CD
∴ ∠D=∠α=45°(两直线平行,同位角相等)
∵ ∠D=∠C
∴ ∠C=45°(等量代换)
∵ AB//CD
∴ ∠C+∠B=180°(两直线平行,同旁内角互补)
∴ ∠B=180°—∠C=135°
随堂练习
如图,已知AC//BD,AE//BF,求证∠A=∠B.请你将括号补充完整.
C
A
B
D
E
F
P
1
证明:∵AC//BD(已知)
∴∠A= ∠1 ( )
∵AE//BF(已知)
∴∠B= ∠1( )
∴∠A=∠B ( )
两直线平行,内错角相等
两直线平行,内错角相等
等量代换
问题解决
如图,从一艘船上测得一个灯塔的方向是北偏西 48°,那么这艘船在这个灯塔的什么方向?
北
东
答案:南偏东48°
1
归纳小结
(1)请你谈谈本节课的收获和感受。
(2)说说平行线的“判定”与“性质”有什么不同?
角的关系(相等或互补)
线的关系(平行)
当堂检测
请你完成《济南市初中数学2020空中课堂学习经历案》上的当堂检测。
课后作业
请你完成《济南市初中数学2020空中课堂学习经历案》上的课后练习题。
数学阅读
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
