北师大版八年级下册数学1.2 直角三角形同步练习(含答案)
文档属性
| 名称 | 北师大版八年级下册数学1.2 直角三角形同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-08 00:00:00 | ||
图片预览


文档简介
北师大版八年级下册数学1.2 直角三角形同步练习
知识要点
1.直角三角形的两个锐角 .
2.有两个角互余的三角形是 三角形.
3.直角三角形两条直角边的平方和 斜边的平方.
4.如果三角形两边的平方和等于第三边的平方,那么这个三角形是 三角形.
5.斜边和一条直角边分别相等的两个 三角形 .
基础训练
1.在△OAB中,∠O=90°,∠A=35°,则∠B=( )
A.35° B.55° C.65° D.145°
2.在△ABC中,若∠B与∠C互余,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列命题的逆命题不正确的是( )
A. 两直线平行,同位角相等 B. 全等三角形的面积相等
C. 面积相等的两个三角形全等 D. 直角三角形两锐角互余
4.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A. a=1.5,b=2,c=3 B. a=7,b=24,c=25
C. a=6,b=8,c=10 D. a=3,b=4,c=5
5.下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
6.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A. 35° B. 55° C. 60° D. 70°
7.已知直角三角形中30°角所对的直角边长为5,则斜边长为( )
A. 5 B. 10 C. 12 D. 13
8.如图,DB⊥AE,AB=DB,AC=DE,则△ABC≌△DBE的依据是( )
A. SAS B. ASA C. AAS D. HL
9. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1 B.+1
C.-1 D.+1
10.如图,AB⊥BC,DC⊥BC,E是BC上一点,∠BAE=∠DEC=60°,AB=3,CE=4.则AD为( )
A.48 B.24 C.10 D.12
11.下列说法正确的有( )
① 两个三角形中,有两条边对应相等,则可以用“HL”来判定这两个三角形全等;
② 有一条直角边和一个锐角对应相等的两个三角形全等;
③ 有两条直角边分别相等的两个直角三角形全等;
④ 两锐角对应相等的两个直角三角形全等.
A. 1个 B. 2个 C. 3个 D. 4个
12.直角三角形三边长为6,8,10,则它斜边上的高为 .
13.命题“如果ab=0,那么a=0,b=0”的逆命题是 .
14.如图,在△ACB中,若AB=AC=5,BC=6,则△ABC的面积为 .
第14题 第15题 第16题
15. 如图1-2-16,AC⊥BC,AD⊥DB,要使△ABC≌△BAD,还需添加条件__________. (只需写出符合条件的一种情况)
16.如图,BE,CF为△ABC的高,且BE=CF,BE,CF交于点H,若BC=10,FC=8,则EC= .
17.在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BE交AD于点F,试说明AE=
AF.
18.如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E,F,那么CE=DF吗?说明理由.
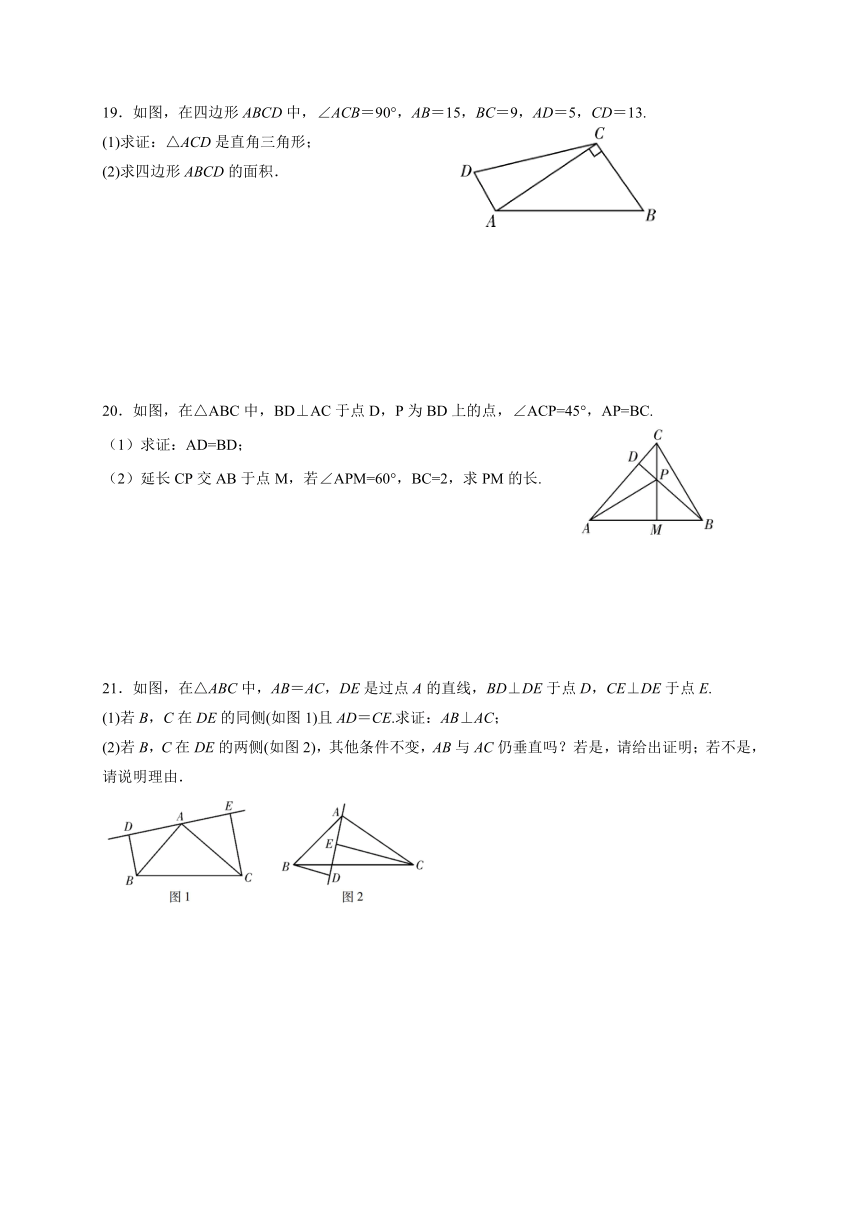
19.如图,在四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,CD=13.
(1)求证:△ACD是直角三角形;
(2)求四边形ABCD的面积.
20.如图,在△ABC中,BD⊥AC于点D,P为BD上的点,∠ACP=45°,AP=BC.
(1)求证:AD=BD;
(2)延长CP交AB于点M,若∠APM=60°,BC=2,求PM的长.
21.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若B,C在DE的同侧(如图1)且AD=CE.求证:AB⊥AC;
(2)若B,C在DE的两侧(如图2),其他条件不变,AB与AC仍垂直吗?若是,请给出证明;若不是,请说明理由.
中考链接
(2018内蒙古包头,8,3分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且
∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为?( )
? A.17.5° ????B.12.5° ????C.12° ????D.10°
(2019北京,12,2分)如图所示的网格是正方形网格,则∠PAB+∠PBA= ????°(点A,B,P是网格
线交点).
?
答案
B
B
B
A
D
D
B
D
D
C
B
4.8
13.如果a=0,b=0,那么ab=0
14.12
15.AC=BD(答案不唯一)
16.6
17.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE.
∵∠BAC=90°,∴∠ABE+∠AEF=90°.
∵DA⊥BC,∴∠CBE+∠BFD=90°,
∴∠AEF=∠BFD.
∵∠BFD=∠AFE,∴∠AEF=∠AFE,
∴AE=AF.
18.解:CE=DF.
理由如下:
在Rt△ABC和Rt△BAD中,
BC=AD,
AB=BA,
∴Rt△ABC≌Rt△BAD(HL).
∴AC=BD,∠CAB=∠DBA.
在△ACE和△BDF中,
∠CAE=∠DBF,
∠AEC=∠BFD=90°,
AC=BD,
∴△ACE≌△BDF(AAS).
∴CE=DF.
19.(1)证明:在△ABC中,
∵∠ACB=90°,AB=15,BC=9,
∴AC= = =12.
在△ACD中,∵AD=5,CD=13,
∴AD2+AC2=52+122=132=CD2,
∴△ACD是直角三角形.
(2)解:四边形ABCD的面积
=△ABC的面积+△ACD的面积
=×AC×BC+×AD×AC
=×12×9+×5×12
=54+30=84.
20.(1)证明:∵BD⊥AC,∠ACP=45°,∴∠DPC=∠DCP=45°.
∴CD=DP.又∵AP=BC,
∴Rt△ADP≌Rt△DBC(HL).
∴AD=BD.
(2)解:∵AD=BD,BD⊥AC,∴∠DAB=∠DBA=45°.
又∵∠CPD=∠BPM=45°,
∴∠PMB=∠PMA=90°.
∵∠APM=60°,∴∠PAM=30°.
∵BC=AP=2,且∠PAM=30°,∴PM=1.
21.(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∴Rt△ABD≌Rt△CAE(HL),
∴∠DAB=∠ECA,∠DBA=∠CAE.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°-(∠BAD+∠CAE)=90°,∴AB⊥AC.
(2)解:AB⊥AC.理由如下:
同(1)可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,
即∠BAC=90°,∴AB⊥AC.
D
45
知识要点
1.直角三角形的两个锐角 .
2.有两个角互余的三角形是 三角形.
3.直角三角形两条直角边的平方和 斜边的平方.
4.如果三角形两边的平方和等于第三边的平方,那么这个三角形是 三角形.
5.斜边和一条直角边分别相等的两个 三角形 .
基础训练
1.在△OAB中,∠O=90°,∠A=35°,则∠B=( )
A.35° B.55° C.65° D.145°
2.在△ABC中,若∠B与∠C互余,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列命题的逆命题不正确的是( )
A. 两直线平行,同位角相等 B. 全等三角形的面积相等
C. 面积相等的两个三角形全等 D. 直角三角形两锐角互余
4.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A. a=1.5,b=2,c=3 B. a=7,b=24,c=25
C. a=6,b=8,c=10 D. a=3,b=4,c=5
5.下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
6.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A. 35° B. 55° C. 60° D. 70°
7.已知直角三角形中30°角所对的直角边长为5,则斜边长为( )
A. 5 B. 10 C. 12 D. 13
8.如图,DB⊥AE,AB=DB,AC=DE,则△ABC≌△DBE的依据是( )
A. SAS B. ASA C. AAS D. HL
9. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1 B.+1
C.-1 D.+1
10.如图,AB⊥BC,DC⊥BC,E是BC上一点,∠BAE=∠DEC=60°,AB=3,CE=4.则AD为( )
A.48 B.24 C.10 D.12
11.下列说法正确的有( )
① 两个三角形中,有两条边对应相等,则可以用“HL”来判定这两个三角形全等;
② 有一条直角边和一个锐角对应相等的两个三角形全等;
③ 有两条直角边分别相等的两个直角三角形全等;
④ 两锐角对应相等的两个直角三角形全等.
A. 1个 B. 2个 C. 3个 D. 4个
12.直角三角形三边长为6,8,10,则它斜边上的高为 .
13.命题“如果ab=0,那么a=0,b=0”的逆命题是 .
14.如图,在△ACB中,若AB=AC=5,BC=6,则△ABC的面积为 .
第14题 第15题 第16题
15. 如图1-2-16,AC⊥BC,AD⊥DB,要使△ABC≌△BAD,还需添加条件__________. (只需写出符合条件的一种情况)
16.如图,BE,CF为△ABC的高,且BE=CF,BE,CF交于点H,若BC=10,FC=8,则EC= .
17.在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BE交AD于点F,试说明AE=
AF.
18.如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E,F,那么CE=DF吗?说明理由.
19.如图,在四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,CD=13.
(1)求证:△ACD是直角三角形;
(2)求四边形ABCD的面积.
20.如图,在△ABC中,BD⊥AC于点D,P为BD上的点,∠ACP=45°,AP=BC.
(1)求证:AD=BD;
(2)延长CP交AB于点M,若∠APM=60°,BC=2,求PM的长.
21.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若B,C在DE的同侧(如图1)且AD=CE.求证:AB⊥AC;
(2)若B,C在DE的两侧(如图2),其他条件不变,AB与AC仍垂直吗?若是,请给出证明;若不是,请说明理由.
中考链接
(2018内蒙古包头,8,3分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且
∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为?( )
? A.17.5° ????B.12.5° ????C.12° ????D.10°
(2019北京,12,2分)如图所示的网格是正方形网格,则∠PAB+∠PBA= ????°(点A,B,P是网格
线交点).
?
答案
B
B
B
A
D
D
B
D
D
C
B
4.8
13.如果a=0,b=0,那么ab=0
14.12
15.AC=BD(答案不唯一)
16.6
17.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE.
∵∠BAC=90°,∴∠ABE+∠AEF=90°.
∵DA⊥BC,∴∠CBE+∠BFD=90°,
∴∠AEF=∠BFD.
∵∠BFD=∠AFE,∴∠AEF=∠AFE,
∴AE=AF.
18.解:CE=DF.
理由如下:
在Rt△ABC和Rt△BAD中,
BC=AD,
AB=BA,
∴Rt△ABC≌Rt△BAD(HL).
∴AC=BD,∠CAB=∠DBA.
在△ACE和△BDF中,
∠CAE=∠DBF,
∠AEC=∠BFD=90°,
AC=BD,
∴△ACE≌△BDF(AAS).
∴CE=DF.
19.(1)证明:在△ABC中,
∵∠ACB=90°,AB=15,BC=9,
∴AC= = =12.
在△ACD中,∵AD=5,CD=13,
∴AD2+AC2=52+122=132=CD2,
∴△ACD是直角三角形.
(2)解:四边形ABCD的面积
=△ABC的面积+△ACD的面积
=×AC×BC+×AD×AC
=×12×9+×5×12
=54+30=84.
20.(1)证明:∵BD⊥AC,∠ACP=45°,∴∠DPC=∠DCP=45°.
∴CD=DP.又∵AP=BC,
∴Rt△ADP≌Rt△DBC(HL).
∴AD=BD.
(2)解:∵AD=BD,BD⊥AC,∴∠DAB=∠DBA=45°.
又∵∠CPD=∠BPM=45°,
∴∠PMB=∠PMA=90°.
∵∠APM=60°,∴∠PAM=30°.
∵BC=AP=2,且∠PAM=30°,∴PM=1.
21.(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∴Rt△ABD≌Rt△CAE(HL),
∴∠DAB=∠ECA,∠DBA=∠CAE.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°-(∠BAD+∠CAE)=90°,∴AB⊥AC.
(2)解:AB⊥AC.理由如下:
同(1)可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,
即∠BAC=90°,∴AB⊥AC.
D
45
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
